Как рассчитать дополнительную функцию ошибок?
тебе программу что ли написать надо?
Я бы считал как \sqrt(pi)/2-интеграл от 0 до X (интеграл ошибок*2/sqrt(pi. Для последнего существует разложение в ряд, но сейчас его уже лень писать.
ДА, мне надо написать программу. Вернее, я ее уже написал, там интеграл считался методом прямоугольников, но сходится медленно, поэтому с нужной точностью (0,1%) считается долго.. А насчет ряда - не знал.. Как ряд выглядит?
) Вопрос: Как ты вычисляешь ошибку - с помощью выкладок на бумажке или методом Рунге?
2)Предложение: Можно слегка усовершенствовать формулу прямоугольников. Например так: \int_a^b = (b-a)*(f(a) + 4fa+b)/2) + f(b/6 . У такой формулы точность на два порядка выше.
2)Предложение: Можно слегка усовершенствовать формулу прямоугольников. Например так: \int_a^b = (b-a)*(f(a) + 4fa+b)/2) + f(b/6 . У такой формулы точность на два порядка выше.
GNU Scientific Library (gsl) смотрел?
http://www.gnu.org/software/gsl/
Ещё: http://www.gnu.org/directory/science/
---
...Я работаю...
http://www.gnu.org/software/gsl/
Ещё: http://www.gnu.org/directory/science/
---
...Я работаю...
да.. ошибку я не вычисляю, я смотрю на относительную разницу двух последних вычисленных интегралов.
По поводу второго предложения - это ведь как-то называется (то ли трапеций, то ли парабол)?
Никаких библиотек не смотрел, так как я не математик и не знал, куда смотреть
Как вообще квалифицированные математики поступают в моем случае? Ведь такой расчет отнимает кучу машинного времени...
Неужели только прямым численным интегрированием это можно решить?
По поводу второго предложения - это ведь как-то называется (то ли трапеций, то ли парабол)?
Никаких библиотек не смотрел, так как я не математик и не знал, куда смотреть
Как вообще квалифицированные математики поступают в моем случае? Ведь такой расчет отнимает кучу машинного времени...
Неужели только прямым численным интегрированием это можно решить?
На самом деле для вычисления интегралов на компе есть целая наука, ЧМЫ называется . На эту тему написано много толстенных книг , так что
Как называется формула - я не знаю. Точно - не формула трапеций. Скорее всего - "по трем точкам". Указанная наука, например, говорит, что если увеличивать число точек на отрезке интегрирования с правильным выбором коэффициентов, то и порядок точности будет расти, что конечно, ускоряет процесс вычислений.
. На эту тему написано много толстенных книг , так что квалифицированные математикине изобретают велосипед, а используют то что всем известно.
Как называется формула - я не знаю. Точно - не формула трапеций. Скорее всего - "по трем точкам". Указанная наука, например, говорит, что если увеличивать число точек на отрезке интегрирования с правильным выбором коэффициентов, то и порядок точности будет расти, что конечно, ускоряет процесс вычислений.
"Большая Сеть" есть?
Почитай ссылки.
Может, всё уже украдено до нас.
Ещё: http://www.gnu.org/directory/libs/
---
...Я работаю...
Почитай ссылки.
Может, всё уже украдено до нас.
Ещё: http://www.gnu.org/directory/libs/
---
...Я работаю...
Бахвалова в библиотеке толмутик возьми 
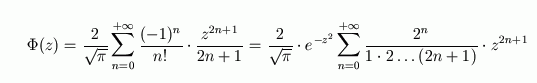
А оценку ошибки не приведёшь?
В смысле, остаточный член, или ограничение на него.
---
...Я работаю...
В смысле, остаточный член, или ограничение на него.
---
...Я работаю...
Не привожу.
Ряды, как правило, считаются, пока S(n+1) не будет равным S(n).
Ряды, как правило, считаются, пока S(n+1) не будет равным S(n).
А ошибки округления?
---
...Я работаю...
---
...Я работаю...
иногда еще пишут длинную вещественную арифметику
но это уже на любителей
но это уже на любителей
Не, нету.
Я не в ЧМах смотрю, а в "специальных функциях".
Но думаю, что знаков 10 будет точных.
Я не в ЧМах смотрю, а в "специальных функциях".
Но думаю, что знаков 10 будет точных.
Хм.
Где-то видел ответственное заявление, что 7 знаков при обычных затратах (IEEE 744?) получить удаётся, но не более.
---
...Я работаю...
Где-то видел ответственное заявление, что 7 знаков при обычных затратах (IEEE 744?) получить удаётся, но не более.
---
...Я работаю...
Может быть.
Я в этом не секу абсолютно. А надо бы...
Я в этом не секу абсолютно. А надо бы...
У кого-то видел пример с суммированием ряда для экспоненты.
При округлении вверх он расходился, что ли.
Чёрт, надо было ссылки сохранять! Теперь фиг найдёшь!
---
...Я работаю...
При округлении вверх он расходился, что ли.
Чёрт, надо было ссылки сохранять! Теперь фиг найдёшь!
---
...Я работаю...
что такое - округление вверх? Округление всегда к ближайшему целому делается
Почитай документацию на (со)процессор.
И ещё исходники glibc.
Да и в Си, по-моему, ничего не сказано про машинную точность и правила округления при вычислении. Как обычно.
---
...Я работаю...
И ещё исходники glibc.
Да и в Си, по-моему, ничего не сказано про машинную точность и правила округления при вычислении. Как обычно.
---
...Я работаю...
Ой не всегда. У сопроцессора, помнится, на то спец. флаги есть.
ну-у... кто ж экспоненту бесконечным циклом вычисляет?.. а с конечным никакого расхождения быть не должно вроде бы.
ЗЫ у сопроцессора есть команда FEXP вроде бы, которая считается правильным образом
а с конечным никакого расхождения быть не должно вроде бы.ЗЫ у сопроцессора есть команда FEXP вроде бы, которая считается правильным образом
Не-а, F2XM1, вычисляет $2^x-1$ для x от 0 до 1 (включительно).
---
...Я работаю...
---
...Я работаю...
ну вот: есть 2^x-1, есть логарифм - все что надо для вычисления экспоненты. Еще нужен код для вычисления 2^N (N - целое)
спасибо!
GLIBC поставляется в исходниках.
Я уже это читал.
---
...Я работаю...
Я уже это читал.
---
...Я работаю...
Хованский, Приложение цепных дробей и их обобщений к вопросам приближенного анализа, М: Гостехиздат, 1956 -- там что-то было
babyborn
Как рассчитать дополнительную функцию ошибок?(интеграл от икс до бесконечности е в степени минус икс квадрат)
Необходимо считать ее с заданной точностью и оптимизировать некие вычисления при полученном значении ДФОШ. Т.е. вариант с таблицей не прокатывает...