Как взять интеграл?
Взять в элементарных вроде получится, а оценка нужна какая?
по частям и замена переменной не помогают, тогда интеграл превращается в еще более страшный. А оценки нужны с обоих сторон
Они нужны асимптотические или везде и какого качества?
А то можно просто (exp{cT)-1)/c оценить, но вряд ли это и требуется
А то можно просто (exp{cT)-1)/c оценить, но вряд ли это и требуется

По идее мне нужно найти u при котором этот интеграл равен некому числу, зависящему от Т. Если, а скорее всего так и есть, нельзя точно вычислить u, или F: F(u,T,с,...)=0, то хотя бы найти её оценки или оценки F, поэтому просто нужны 2 функции от (Т,u) или (u) которые точнее будут приближать график с обох сторон. Сойдет и оценка подинтегральной функции, как ф-ии от u. Главное чтоб они были как можно ближе друг к другу, чем ближе - тем лучше. Если сможешь любой точности достигнуть, без приближения прямыми - считай что ты гений.
P.S. известно как оценить интеграл
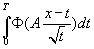
и
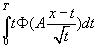
но хотельсь бы оценку c=Т и с=0 улучшить
P.S. известно как оценить интеграл
и
но хотельсь бы оценку c=Т и с=0 улучшить
а) C t^2 также нельзя уже оценить?
б) Если взять исходный по частям, то подынтегральная функция будет хоть и уродская, но вполне даже выражающаяся в элементарных. Может ее можно оценить достаточно для твоих изысканий
б) Если взять исходный по частям, то подынтегральная функция будет хоть и уродская, но вполне даже выражающаяся в элементарных. Может ее можно оценить достаточно для твоих изысканий
будет нечто похожее на
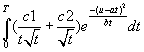
думаю что ее оценить не легче
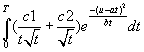
думаю что ее оценить не легче

Используй вторую теорему о среднем, или разложение экспоненты в ряд Тейлора с остаточным членом в форме Лагранжа.
Вряд ли поможет.
Первое по сути, второе потому, что с x^2 он уже не умеет
Первое по сути, второе потому, что с x^2 он уже не умеет
Интеграл от Ф*t^n оценивается по второй теореме о среднем через оценку интеграла от Ф или Ф*t, и т. д.
Оценивается через промежуточную точку. А какую - непонятно. Хорошую оценку как получить?
в окресности какой точки раскладывать? Думаю такой вариант не прокатит
Ф — разве не функция Лапласа? И не монотонна?
Раскладывать экспоненту следует в нуле.
Раскладывать экспоненту следует в нуле.
просто нужны 2 функции от (Т,u) или (u) которые точнее будут приближать график с обох сторон.Ну так ведь Ф монотонно возрастает, её можно оценить сверху её значением при max значении сложного агрумента, от которого она зависит, на промежутке [0,T], и вынести эту верхнюю грань из-под интеграла. Получится оценка сверху. Аналогично оценил бы и снизу.
тогда до какого ж n нужно разложить, чтоб погрешность начала падать. Если у нас Т>>1

Взять +- сколько-то sigma для Ф(x и заменить её значение при стремлении x к +-бесконечности константами, причём для оценки сверху-снизу можно брать разные константы (для точности думаю есть асимптотические ряды по убывающим экспонентам, только потставлять туда что у тебя в Ф аргументом заколебёшься). А в окрестности x=0 рядом Тейлора для склейки. Тогда все произведения на exp(-ct) считаются.
Я бы вообще заменил Ф(x) ломаной сверху и снизу, подставить твой аргумент в эту ломаную. С exp(-ct) всё не посчитается?
Я бы вообще заменил Ф(x) ломаной сверху и снизу, подставить твой аргумент в эту ломаную. С exp(-ct) всё не посчитается?
Разлагать убывающую экспоненту по степеням t бестолковое занятие, т.к. это типичный пример для численных методов, посчитай exp(-20.) с помощью ряда Тейлора. Сколько надо взять n, чтобы члены ряда начали убывать по модулю. В аналитике эти грабли тоже есть.
По-моему, чел не воспринимает того, что ему пишут.
Либо читает посты только от Васи и Пети.
Ну да это его дело, а задачка сама по себе любопытная.
Правда, криво поставлена, и приходится додумывать самому.
Не знаю, для грубой оценки up & down я всё ж вынес бы из-под
крючка именно max и min Ф, соответственно, как и написал выше.
Мотив тот, что Ф (я правильно понял, что это интеграл ошибок?)
монотонна и достаточно быстро достигает своих предельных
значений.
Либо читает посты только от Васи и Пети.
Ну да это его дело, а задачка сама по себе любопытная.
Правда, криво поставлена, и приходится додумывать самому.
Не знаю, для грубой оценки up & down я всё ж вынес бы из-под
крючка именно max и min Ф, соответственно, как и написал выше.
Мотив тот, что Ф (я правильно понял, что это интеграл ошибок?)
монотонна и достаточно быстро достигает своих предельных
значений.
По-моему, чел не воспринимает того, что ему пишут.напротив воспринимаю, тока ничего не пишу на такие догадки типо - взять максимум и минимум ф-ии и тупо подставить, такие оценки яб давно получил, и не спрашивал бы тут. Тока понта от них мало, весь сок в том, что вторая эта величина должна существенно зависеть от Ф а то вся оценка сводится- от нуля до бесконечности. Потом вариант с ломаными тоже не серъезен, я о нем сразу написал, что он не нужен, по сути он является не аналитическим, а из числа численных методов подсчета. Тупо можно разбит [0,T] на n промежутков и в каждом подставить значение ti в подинтегральную ф-ю, и сказать - "хотим точности - увеличиваем n".
В итоге мне нужно получить числа, а не метод их подсчета.
Мотив тот, что Ф (я правильно понял, что это интеграл ошибок?)Да, очевидно cumulative density for a standart normal distribution
Ф(x)=
= \frac{1}{sqrt{2\pi}} \int_{-\infty}^{x} exp(-\frac{y^2}{2}) dy
=1/2 erf(x/sqrt(2 + 1/2
задача:
нужно минимизировать величину D(u) u>=0
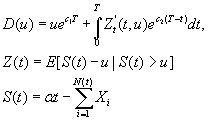
X,N(t) - случайные величины, 0<c1<c2 ~ 0.05..0.3
T>0, E[S(t)]>0
нужно минимизировать величину D(u) u>=0
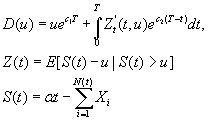
X,N(t) - случайные величины, 0<c1<c2 ~ 0.05..0.3
T>0, E[S(t)]>0
Не так, вы просто не поняли, что имелось в виду.
Оценки сверху и снизу типа Ф(f(T,u * интеграл от обычной экспоненты по промежутку [0,T],
который элементарно берется, имеют смысл, и не являются оценками от 0 до +inf.
Полезны они вам или нет - это другой вопрос, это уж вы сами думайте, или уточняйте постановку
задачи. Во всяком случае, эликсира вам пока тут не предложили, и вряд ли предложат.
Оценки сверху и снизу типа Ф(f(T,u * интеграл от обычной экспоненты по промежутку [0,T],
который элементарно берется, имеют смысл, и не являются оценками от 0 до +inf.
Полезны они вам или нет - это другой вопрос, это уж вы сами думайте, или уточняйте постановку
задачи. Во всяком случае, эликсира вам пока тут не предложили, и вряд ли предложат.
я когда писал, надеялся, что может кто-то сталкивался с подобными интегралами, и знает где искать их оценки
Знаете, если это "вам задали", то ответ, наверное, есть, так что не мучьте
себя. Иначе б не задавали.
А если это задача "из жизни", то с ответом может быть реальная напряженка.
Потому форум и молчит.
Поверьте опыту, я, хоть и не математик по образованию, не одну оценку
в своей жизни сделал, когда нужно было, и всюду приходилось ограничиваться
подручными средствами. И наиболее "примитивные", на первый взгляд, идеи
зачастую бывали наиболее плодотворными.
Если вам именно асимптотику получить надо - определите, какой параметр у вас
к чему устремляется, и поизучайте асимптотические методы оценки интегралов.
Особенно полезно полистать учебники комплана. Метод перевала, например.
Если же вам достаточно простой двухсторонней оценки в виде неравенства -
не ищите сложных, ограничьтесь самыми простыми. Вот и весь совет.
себя. Иначе б не задавали.
А если это задача "из жизни", то с ответом может быть реальная напряженка.
Потому форум и молчит.
Поверьте опыту, я, хоть и не математик по образованию, не одну оценку
в своей жизни сделал, когда нужно было, и всюду приходилось ограничиваться
подручными средствами. И наиболее "примитивные", на первый взгляд, идеи
зачастую бывали наиболее плодотворными.
Если вам именно асимптотику получить надо - определите, какой параметр у вас
к чему устремляется, и поизучайте асимптотические методы оценки интегралов.
Особенно полезно полистать учебники комплана. Метод перевала, например.
Если же вам достаточно простой двухсторонней оценки в виде неравенства -
не ищите сложных, ограничьтесь самыми простыми. Вот и весь совет.
Из оценки Гаусса остаточного члена гамма-функции Эйлера следует, что для убывания хватит n = 20.*e; для численных методов это действительно много, я не подумал про большие T, и дал неправильный совет. Разлагать в нуле не следует.
можно к оценке этого интервала свести
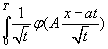
нужно его оценить или свести к
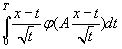
нужно его оценить или свести к
Потом вариант с ломаными тоже не серъезен, я о нем сразу написал, что он не нужен, по сути он является не аналитическим, а из числа численных методов подсчета. Тупо можно разбит [0,T] на n промежутков и в каждом подставить значение ti в подинтегральную ф-ю, и сказать - "хотим точности - увеличиваем n".С какой стати-то?
В итоге мне нужно получить числа, а не метод их подсчета.
Берущиеся интегралы
\int_0^s 1/\sqrt(t) exp(-t) dt = \sqrt{\pi} erf(\sqrt{s})
\int_0^s exp(-t) dt = 1 - exp(-s)
\int_0^s \sqrt(t) exp(-t) dt = \sqrt{\pi} erf(\sqrt{s}) / 2 - \sqrt{s} exp(-s)
Естественно \int_a^b = \int_0^b - \int_0^a
Значит если оценить сверху и снизу Ф(x) двумя кусочно-линейными функциями (постоянны на крайних участках где x стремится к бесконечности)
\sum_i (k_i x + b_i) * I(a_i,b_i
где
I(a_i,b_i) - индикатор отрезка [a_i,b_i] равный 1 при x \in [a_i,b_i] и 0 вне его
то по всем отрезкам интегралы посчитаются аналитически.
Отрезки для оценки сверху и снизу можно разные взять. Вообще можно одну оценку построить, вторая в силу нечётности erf(x) получится из симметрии.
Оценка может не быть непрерывной функцией. Ну для начала для простоты в силу монотонного возрастания Ф(x) берём кусочно-постоянную функцию для оценки сверху
Ф(x) < Ф(-3) * I(-\infty, -3) + Ф(-2) * I(-3, -2) + Ф(-1) * I(-2, -1) + Ф(0) * I(-1, 0) +
+ Ф(1) * I(0, 1) + Ф(2) * I(1, 2) + Ф(3) * I(2, 3) + Ф(\infty) * I(3, \infty)
Всё сведётся к \int_0^s exp(-t) dt = 1 - exp(-s) по нескольким отрезкам и erf от концов отрезков не вылезет.
Не устраивает что получится?

agszao
a>=0
или где можно найти его оценку?
Ф ~ N(0,1)