Сгладить функцию Z(X,Y)
Ну какой-нить метод наименьших квадратов + конечные элементы... Если дашь файл с таблицей(plain text то может я даже смогу приспособить свою прогу, которую для Богачева делал 

>С помощью каких программ можно сделать так, чтобы рисунок стал непрерывным, гладким и остался более-менее похож на исходный?
Не очень понятно, чего сглаживать надо -- рисунок или функцию
>Какую аппроксимацию выбрать?
например сплайнами. или фурье. выбор типа аппроксимации часто зависит от дополнительных оценок функции, типа порядок гладкости и т.д.
>С помощью какой программы сам процесс наиболее безболезненный?
любой матпакет, например матлаб. безболезненный -- это типа так теперь погрешность называется?
Не очень понятно, чего сглаживать надо -- рисунок или функцию

>Какую аппроксимацию выбрать?
например сплайнами. или фурье. выбор типа аппроксимации часто зависит от дополнительных оценок функции, типа порядок гладкости и т.д.
>С помощью какой программы сам процесс наиболее безболезненный?
любой матпакет, например матлаб. безболезненный -- это типа так теперь погрешность называется?

Вот исходные данные в формате x,y,z.
безболезненный -- это типа так теперь погрешность называется?Безболезненный - значит камлания с бубнами как можно меньше.
Не получается.  И как я в свое время ее сдал, ума не приложу
И как я в свое время ее сдал, ума не приложу 
 И как я в свое время ее сдал, ума не приложу
И как я в свое время ее сдал, ума не приложу 
тогда смотри в сторону interp2 в матлабе.
С помощью gnuplot'a получилось вот так:
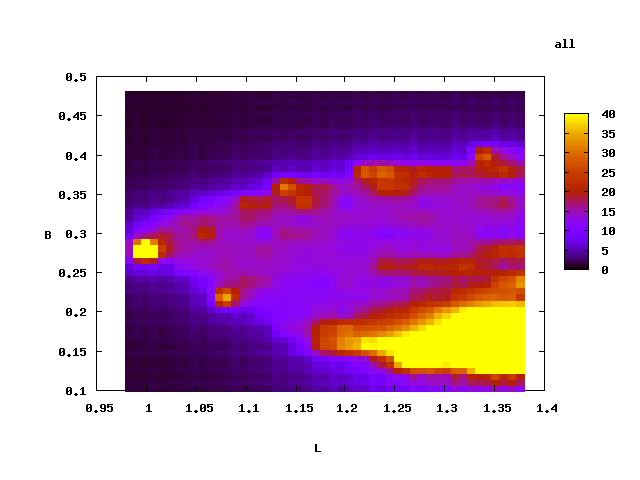
Это некое усреднение с весом, обратно пропорциональным расстоянию до точки...

Это некое усреднение с весом, обратно пропорциональным расстоянию до точки...
откуда расстоянию?
Есть набор экспериментальных точек x1,y1,x2,y2...xn,yn и значения функции z1,z2,...zn
Есть точка (x,y в которой мы хотим найти значение новой (гладкой) функции.
Это значение функции строится как среднее арифметическое всех значений zi поделенных на некоторый коэффициент, зависящий от расстояния до (x,y). Этот коэффициент выглядит как нечто вроде (x-xi)^n + (y-yi)^n. Степень n>0 является параметром.
По крайней мере, так я понял описание функции dgrid3d
(исправления были, неправильно вспомнил описание)
Есть точка (x,y в которой мы хотим найти значение новой (гладкой) функции.
Это значение функции строится как среднее арифметическое всех значений zi поделенных на некоторый коэффициент, зависящий от расстояния до (x,y). Этот коэффициент выглядит как нечто вроде (x-xi)^n + (y-yi)^n. Степень n>0 является параметром.
По крайней мере, так я понял описание функции dgrid3d
(исправления были, неправильно вспомнил описание)
Слушай - у нас в радиоинтерферометрии похожая задача есть! На плоскости - значения функции в произвольных точках (в ограниченной области). Для FFT надо иметь сетку => CНачала свертывают эту функцию с какой-то гладкой, затем находят значение сглаженной в нужных местах. Ща гляну в "библию" - мож там есть что-то непосредственно нужное тебе?
OK. Буду очень рад, если сделаем свою программу и не будем полагаться на хрен знает какой алгоритм в чужих программах.
Слушай - а ты для функции аргументов L,B случайно нигде Фурье Преобразование не используешь? Или просто надо сгладить? У нас то фишка в том, что задача сводиться к нахождению значений величины в узлах сетки, если известны ее значения где-то в произвольных местах (по сути - обратно к твоей задаче). Причем на самом деле для чего необходимо распределение значений этой величины на сетке - чтоб FFT ее в нужную нам величину (изображение). Это делается сверткой с гладкой функцией, а FT этого - это произведение их FTs. Артифактом FFT остается повторяемость того, что получилось по интервалам, обратным шагу используемой сетки. И вот тут вводят критерии того, какая должна быть свертывающая функция - ее FT должно быть постоянным, а затем резко спадать, чтоб не было повторений.
В твоем случае видно, что данные вроде как расположены на сетке?
В твоем случае видно, что данные вроде как расположены на сетке?
А X,Y - это что? Просто почему должны одни величины влиять на другие, которые реально не связаны? Просто если бы у тебя была гауссиана "оцифрованная" - то этот алгоритм с обратным квадратом расстояния ее б размазал по полю. А есть величины ошибок функции?
Ну, нигде в наших экспериментах фурье-преобразование не делается. Может быть сама природа его где-то делает? 
Функция моя - это зависимость потока частиц от координат некоторого пространства. Вот смотри - есть радиационные пояса, в них частицы (протоны) летают. Грубо говоря их поток зависит от расстояния до Земли (L) и широты (B). То, что L выражено в радиусах Земли, а B в гауссах, это тебя волновать не должно
С физической точки зрения потоки в двух близлежащих точках пространства L,B должны быть близки, т.е. функция гладкая. Частицы перемещаются из одной точки этого пространства в другие (есть колебания вдоль B в разные стороны и монотонный дрейф в сторону уменьшения L т.е. значения функции в одной точке могут быть связаны со значениями этой же функции в другой точке.

Функция моя - это зависимость потока частиц от координат некоторого пространства. Вот смотри - есть радиационные пояса, в них частицы (протоны) летают. Грубо говоря их поток зависит от расстояния до Земли (L) и широты (B). То, что L выражено в радиусах Земли, а B в гауссах, это тебя волновать не должно

С физической точки зрения потоки в двух близлежащих точках пространства L,B должны быть близки, т.е. функция гладкая. Частицы перемещаются из одной точки этого пространства в другие (есть колебания вдоль B в разные стороны и монотонный дрейф в сторону уменьшения L т.е. значения функции в одной точке могут быть связаны со значениями этой же функции в другой точке.
Ну, нигде в наших экспериментах фурье-преобразование не делаетсяI mean: может эти данных надо FT!
Хм... моя задача - сгладить эту функцию, а не получить ее FT-образ.
Функция получена усреднением экспериментальных данных по квадратикам. Мы уверены, что она гладкая, однако не совсем удачный набор экспериментальных данных ограничивает нас в возможностях.
Функция получена усреднением экспериментальных данных по квадратикам. Мы уверены, что она гладкая, однако не совсем удачный набор экспериментальных данных ограничивает нас в возможностях.
Функция получена усреднением экспериментальных данных по квадратикамА не усредненные по квадратикам данные еще живы?
Конечно, живы.
Так зачем их было по квадратам усреднять? Что нить типа "2D медианного фильтра" может?
Может быть. К сожалению, не знаком с тематикой. Что это такое?
Ну что-нить типа как взять какую-нить окружность - посчитать сумму значений попадающих в нее точек. Отсюда получить cреднюю величину характеризующую искомое значение функции в точке центра окружности. Чуть передвинуть на расстояние <<R - еще так же... Наверно достаточно гладко будет?
У него похоже сейчас на место каждой точки лепится прямоугольник с бленидингом. А чтобы сделать как ты сказал, придется повозиться. KD-tree, и все такое  У меня есть, если что.
У меня есть, если что.
 У меня есть, если что.
У меня есть, если что.может фильтром фотожопа - размытие какое нить? =)
прояви художественную смекалку ! почесав тыковку
прояви художественную смекалку ! почесав тыковку
Есть программа Surfer6 - она может и сгладить кучей способов, и нарисовать тоже.
Всем рекомендую!
Всем рекомендую!
Спасибо. Я ей и рисовал первый из графиков. К сожалению, мои религиозные взгляды не позволяют мне пользоваться программой, которая искажает мои данные. Делаю, я к примеру grid data потом, contour. А у меня появляется вместо одного максимума два. И ни один из них не лежит там, где был максимум в исходных данных. Ну нафиг, нафиг.
Кроме того, при делании grid'a нужно выбирать метод усреднения. А там нормальных-то и нету.
Kriging кажется нормальным до поры до времени.
Кроме того, при делании grid'a нужно выбирать метод усреднения. А там нормальных-то и нету.

Kriging кажется нормальным до поры до времени.

yurimedvedev
Есть вот такая экспериментальная зависимость:Цветом показано значение Z(X,Y) согласно легенде.
С помощью каких программ можно сделать так, чтобы рисунок стал непрерывным, гладким и остался более-менее похож на исходный? Я так понимаю, это задача аппроксимации. Какую аппроксимацию выбрать? С помощью какой программы сам процесс наиболее безболезненный?