Измеримое по Лебегу множество
Множество A называется измеримым по Лебегу, если
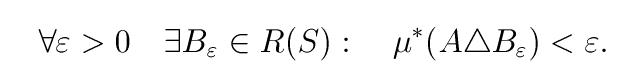
где R(S) - кольцо, порожденное полукольцом S (в случае классической меры Лебега S состоит из прямого произведения полуинтервалов: S = { |---)^n } ). Далее по известной теореме мера однозначно продолжается на сигма-алгебру, натянутую на R(S - сигма-алгебру измеримых множеств.
Вроде так.
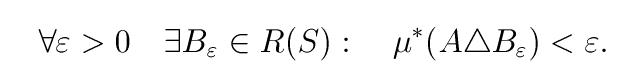
где R(S) - кольцо, порожденное полукольцом S (в случае классической меры Лебега S состоит из прямого произведения полуинтервалов: S = { |---)^n } ). Далее по известной теореме мера однозначно продолжается на сигма-алгебру, натянутую на R(S - сигма-алгебру измеримых множеств.
Вроде так.
спасибо 
Да не за что Петр Анатольевич крепко этому научил
Петр Анатольевич крепко этому научил Вот завтра и проверим у ПА, насколько точно ты помнишь определение
А пример неизмеримого по Лебегу множества кто-нибудь знает?
вроде бы из канторовой лестницы делается
alpha - иррац. число, окружность длины 1. Все точки делим на классы по поворотам окружности на углы Pi*alpha*n, n-целое. Каждый класс - счётное мн-во точек. Выберем из каждого класса по одной точке, полученное мн-во неизмеримо.
Из канторовской лестницы можно доказать, что такое множество существует...
нет, не так. через канторовскую лестницу доказывается существование неизмеримой функции.
И обычно не борелевское измеримое множество строится.
а она сама по себе не является неборелевским измеримым? 
во, точно 
балда я 
балда я не-а 
оно же измеримо...
канторовская лестница -- функция. 
сама по себе она измерима и по Борелю... нужно меру "дырок" сделать ненулевой, тогда только по Лебегу. вроде так
да она непрерывна на [0,1], а дифф. почти всюду, вы чего тут за флуд развели
нет, как была непрервной, так и останется
отстань. нафлудишь с наше - будешь командовать.
да ну? 
когда там разрывы в явном виде строятся?
когда там разрывы в явном виде строятся? Канторовская лестница - непрерывная почти всюду функция! У меня книжка в свидетелях!
пипец. я же сказал - взяли канторовскую лестницу, но нестандартную, а "дырявую", на "дырках" нужно добиться разрывов ненулевой меры(чтобы С-свойство нарушилось в частности, можно повторить там ту же процедуру. получится фрактал(не помню, как называется, но довольно известный)
характеристическая функция канторовского множества положительной меры получиться
>характеристическая функция канторовского множества положительной меры получиться
значит так
во-первых, получится
а во-вторых, конечно же получится нечто более сложное
значит так
во-первых, получится
а во-вторых, конечно же получится нечто более сложное
А пример неизмеримого по Лебегу множества кто-нибудь знает?Если до сих пор и очень надо, то могу привести пример, в построении используется аксиома выбора...
Ага, а ещё кроме классического примера Витали есть пример неизмеримого множества Т. П. Лукашенко.
Только его долго постить
Только его долго поститьА где его найти можно? Хочется посмотреть.
Или запости, если не влом
Или запости, если не влом
влом.
Там страницы 3 построение, как я это запощу ? Спроси у автора лучше
его на мехмате легко найти
PS А если тебе нужны примеры неизмеримых множеств, то их много немало собрано в книге
Богачёва "Основы теории меры", недавно вышла.
Там страницы 3 построение, как я это запощу ? Спроси у автора лучше
его на мехмате легко найти
PS А если тебе нужны примеры неизмеримых множеств, то их много немало собрано в книге
Богачёва "Основы теории меры", недавно вышла.
Ну так постить или нет?
я сдала уже экзамен
Вот завтра и проверим у ПА, насколько точно ты помнишь определение
Ну как, правильно? Что сдавала, как сдала?
ничего из того, что обсуждалось в этом треде, мне не понадобилось.
Понадобился контрпример к теореме Лузина и пришлось придумывать доказательство того, что из любого покрытия множества в R^n можно выбрать не более чем счетное подпокрытие.
Понадобился контрпример к теореме Лузина и пришлось придумывать доказательство того, что из любого покрытия множества в R^n можно выбрать не более чем счетное подпокрытие.
Из любого?
открытыми множествами, конечно
а что за предмет сдавала?
Действительный анализ, конечно
Mike3
кто-нибудь может привести точное определение измеримого по Лебегу множества в случае классической Лебеговой меры в R^n? \\