Производная от дельта-функции

klushka1

Встретил в Maple описание функции Дирака:

Derivatives of the Dirac function are denoted by the two-argument Dirac function. The first argument denotes the order of the derivative. For example, diff(Dirac(t t$n) is automatically simplified to Dirac(n, t) for any integer n.

Что представляет из себя n-ая производная дельта-функции?

stm7537641

n-я производная дельта-функции -- это функционал, который на основной функции f принимает значение (-1)^n*f^{(n)}(0).

avgustinka

В чём проблема? Обычная производная обобщённой функции: (f',ф):=(f,-ф').

Mailer

дельта функция Дирака-обобщённая функция,или линейный непрерывный функционал на D/
По определению ф.Дирака: (dirac,fi)=fi(0)
(dirac',fi)=fi'(0)
надо думать: (dirac n-го порядка,fi)=fi'''...(0) (производная n-го порядка)
или ещё домножить надо на (-1)^n ?

stm7537641

знаки забыли -- определение производной об. ф-ции выше дано

klushka1

То есть int (dirac(n,t)*f(t=(-1)^n*f(n-ая производная0)
А график производной дельта-функции как выглядит?
//Сорри за глупые вопросы, я не математик

Mailer

как график выглядит,не знаю
я тоже не математик)

NHGKU2

Дельта-функция и её производные - не регулярные обобщённые функции.
График их нарисовать нельзя
И int (dirac(n,t)*f(t=(-1)^n*f(n-ая производная0) - это чушь, такое равенство можно написать только для регулярных ОФ.

stm7537641

А график производной дельта-функции как выглядит?

Продифференцируйте дельта-образную последовательность

klushka1

То есть это тоже неправильно?

n-я производная дельта-функции -- это функционал, который на основной функции f принимает значение (-1)^n*f^{(n)}(0).

При n=0 это равенство выполняется

parfum74

Ну, типа, как тут написали, формально операция интегрирования не определена ни для производных дельта функции, ни для нее самой, т.к. они не входят в пространство, где эта операция определяется. Но если писать не с интегралом, а ввиде скалярного произведения, то написанное равенство будет верным.
Насчет графика. Ты можешь нарисовать график дельта функции?

klushka1

Продифференцируйте дельта-образную последовательность

Что это такое?

stm7537641

График их нарисовать нельзя

Ну хоть физический смысл она имеет?
---
"Я с дрожью ужаса отворачиваюсь от ваших несчастных проклятых функций, у которых нет производных." (Шарль Эрмит)

NHGKU2

Это-то правильно.
Чушь - это то, что значение функционала ф на функции f равно int (ф(t)*f(t. Если функционал ф регулярный, то этому равенству еще можно придать смысл (ф соответствует основная функция Ф, и тогда <ф,f>=\int Ф(t)f(t)dt а если он не регулярный, как например дельта-функция, то аналогичного равенства нет.

klushka1

Насчет графика. Ты можешь нарисовать график дельта функции?

Схематически :
dirac(t)=0, t!=0;
dirac(t)=inf, t==0

klushka1

Это-то правильно.
Чушь - это то, что значение функционала ф на функции f равно int (ф(t)*f(t. Если функционал ф регулярный, то этому равенству еще можно придать смысл (ф соответствует основная функция Ф, и тогда <ф,f>=\int Ф(t)f(t)dt а если он не регулярный, как например дельта-функция, то аналогичного равенства нет.

Возразить ничего не могу, но если я заменю int на скалярное произведение - это будет правильно?

NHGKU2

Физики говорят, что дельта-функция - это такая функция, которая везде кроме нуля равна 0, а в нуле - бесконечности, но тем не менее интеграл от неё по всей прямой равен 1

NHGKU2

Да

stm7537641

Что это такое?

См. Ленг "Математические беседы для студентов", стр. 88 например или Арнольд "Лекции об ур-ниях с частными производными" стр 90.

stm7537641

stm7537641

Т.е. "график" производной дельта-функции выглядит примерно так (сорри за качество):

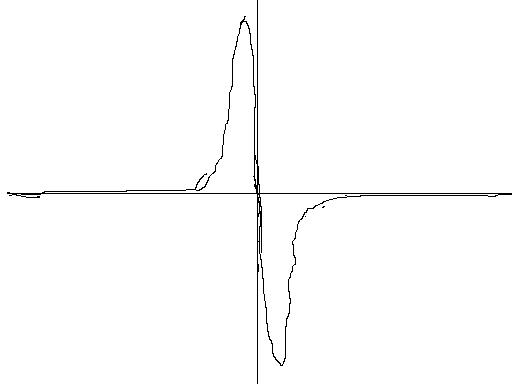
Интересно вспомнить физический смысл (типа диполь -- потенциал двойного слоя )

klushka1

спасибо.

sergeychik_a

ИМХО "график" следует зеркально отбразить отн-но оси у

kachokslava

Примерно раз в семестре поднимается подобный вопрос, и каждый раз обсуждение этого феномена (производной от дельта-функции) перерастает во флуд постов на 200.
Предлагаю авторам и зантересованным лицам переботать архив раздела (поиском пользуйтесь чтобы не продолжать (а он уже начался) флуд здесь.

Togar

Не на собственно скалярное произведение, а на обозначение, похожее на скалярное произведение. В математическом смысле эта операция скалярным произведением не является, т.к. ее операнды берутся из разных пространств. Для обобщенных функций вообще не определено скалярное произведение, либо я чего-то не в курсе.

bububa

ВЫ ЧТО СМЕЕТЕСЬ? Я ТОЖЕ НЕ МАТЕМАТИК, НО ЗНАЮ, ЧТО ПРОИЗВОДНАЯ ОТ ДЕЛЬТА-ФУНКЦИИ ИМЕНУЕМАЯ СЕБЯ ФУНКЦИЕЙ ДИРЕКА-ЭТО ОБЫЧНАЯ СТУПЕНЬКА!НУ ВЫ БЛИН ДАЕТЕ ПОНАРИСОВАЛИ ТАМ

NHGKU2

Ты ошибаешься: "ступенька" (тэта-функция) - это не производная, а первообразная дельта-функции.

bububa

НУ ВЫ БЛИН ДАЕТЕ. ЧЕМУ ЖЕ МЕНЯ НА МАТАНЕ УЧИЛИ?НАРИСОВАТЬ НЕЛЬЗЯ?ДЕЛЬТА-ФУНКЦИЯ-БЕСКОНЕЧНОСТЬ В НУЛЕ. ЕЕ ПРОИЗВОДНАЯ - 0 ДЛЯ {X<0} И 1 ДЛЯ {X>0}!СТУПЕНЬА ЭТО! ИЛИ Я С УМА СОШЛА

bububa

НЕТ НУ ЧЕМУ ЖЕ МЕНЯ УЧИЛИ!

zuzaka

подумай сама

NHGKU2

Ты просто путаешь, наверное.
Ничего страшного. Подумай, и всё поймёшь

parfum74

Не на собственно скалярное произведение, а на обозначение, похожее на скалярное произведение.

Стопудов. Эта операция по-нстоящему называется сверткой.

parfum74

ИЛИ Я С УМА СОШЛА

Раз ты все время пишешь таким крупым шрифтом то однозначно - да (кстати на большие буквы уходит больше интернета, подумай над этим )

bububa

в локалке?

bububa

так пишу маленькими буквами: дельта-функции и есть функция дирека, а функция хевисайда она же ступеька есть первообразная от функции дирека. ну все, у меня точно крыша поехала

kachokslava

правильнее писать (и говорить) функция Дирáка

sergeychik_a

во, когда маленькими буквами пишешь все правильно получаеся