ГОСЫ мехмата МГУ
Ну давай обсудим  Ты что-нибудь знаешь?
Ты что-нибудь знаешь?
 Ты что-нибудь знаешь?
Ты что-нибудь знаешь?а, вот.
знает кто, какого плана задачи будут давать на госах: теоретические или вычислительные?
знает кто, какого плана задачи будут давать на госах: теоретические или вычислительные?
ну здесь в прошлом году обсуждали
я думаю могут быть задачи типа: привести пример такой функции и т.д.
я думаю могут быть задачи типа: привести пример такой функции и т.д.
ссылку можешь дать на этот тред?
а то, что тут названо, задачей не является, строго говоря )
а то, что тут названо, задачей не является, строго говоря )
надо искать, позже попробую
попробуй - смотри окресность прошлого года
попробуй - смотри окресность прошлого года
проклятье, они будут вычислительные.
блин, теперь и методы решения надо откуда-то ботать...
апд: вот еще тред, для смеха )
блин, теперь и методы решения надо откуда-то ботать...
апд: вот еще тред, для смеха )
В последнем треде 3 как я понимаю задачи и вопросы давали до экзамена ? что-то все так четко и дружно спрашивают....
или это они сидели на экзамене с ноутами?
или они не сдали и им просто интересно стало после экзамена как решаются задачи?
или это они сидели на экзамене с ноутами?
или они не сдали и им просто интересно стало после экзамена как решаются задачи?
Сим удостоверяется, что в pdf-ке с материалами по госам в доказательстве теоремы о неявной ф-и, начиная с самого верха страницы 14, идет лажа. Рекомендуется этот момент ботать по Зоричу.
(более точно: практически без объяснения строится отображение Ф из (m иксовых координат и одна координата u) в набор из первых (n-1) координат u, непонятно откуда взявшееся)
(более точно: практически без объяснения строится отображение Ф из (m иксовых координат и одна координата u) в набор из первых (n-1) координат u, непонятно откуда взявшееся)
а я бы порекомендовал книжку Архипов,Чубариков,Садовничий - там все доказывается коротко, конструктивно, и без лишней воды
давайте только различать ГОС механиков и математиков
Подписывайте в сообщении о каком потоке идёт речь
Подписывайте в сообщении о каком потоке идёт речь
Силами товарисча Швиллера в материалах по математике был обнаружен еще один баг!
В самом первом билете в доказательстве теоремы о промежуточном значении пишется выражение вида f(a_k)<x<f(b_k). Но, например, для монотонно убывающих функций это неверно. На самом деле здесь, очевидно, подразумевается "x \in Im[a_k,b_k]", т.е. имеется в виду именно отношение включенности. Take heed.
В самом первом билете в доказательстве теоремы о промежуточном значении пишется выражение вида f(a_k)<x<f(b_k). Но, например, для монотонно убывающих функций это неверно. На самом деле здесь, очевидно, подразумевается "x \in Im[a_k,b_k]", т.е. имеется в виду именно отношение включенности. Take heed.
Не, там все нормально. В формулировке теоремы мы предположили, что f(a) < f(b) и в дальнейшем соотношение не нарушалось
"x \in Im[a_k,b_k]",На самом деле баг там всё же есть. А именно надо писать отрезок, соединяющий f(a) и f(b а не образ [a,b]
по-моему, там доказательство теоремы Кантора о равномерной непрерывности неправильное
Сим удостоверяется, что в pdf-ке с материалами по госам в доказательстве теоремы о неявной ф-и, начиная с самого верха страницы 14, идет лажа. Рекомендуется этот момент ботать по Зоричу.Может у нас разные пдфки, но у меня в пдфке все тип-топ
Для построения отображений Ф_i необходимо иметь n-1 функцию вида F(x_1,x_2,...,x_n, u_i, u_n)=0. Откуда вообще таким функциям взяться?
В билете нет проса о системе неявных функций, так что можешь не заморачиваться.
Ты о неявной функции или о неявном отображении?
В неявном отображении выкидывается одна функция (первая) и последняя переменная, а для остальных применяется предположение индукции, каждая из них удоветворяет условиям теоремы. А потом рассматривается значение этой самой первой функции на наборе и к ней применяется теорема о неявной функции. И в построении все на этом.
А в неявной функции вообще все просто.
В неявном отображении выкидывается одна функция (первая) и последняя переменная, а для остальных применяется предположение индукции, каждая из них удоветворяет условиям теоремы. А потом рассматривается значение этой самой первой функции на наборе и к ней применяется теорема о неявной функции. И в построении все на этом.
А в неявной функции вообще все просто.
скинь-ка мне свою pdf-ку в . <_<
то, что ты говоришь, вроде правильно, но в моей pdf-ке все не так.
да, неявное отображение имелось в виду
то, что ты говоришь, вроде правильно, но в моей pdf-ке все не так.
да, неявное отображение имелось в виду
В 6 билее лажа. В первом доказательстве берем a_k=|x_k|+x_k, а потом говорим, что a_k<|x_k| — это лажа полная. Видимо надо брать a_k=(|x_k|+x_k)/2, тогда a_k<=|x_k|. Про b_k аналогично
Вот еще забыл. Самый конец стр.30, лемма о предельном переходе в собственном интеграле. Само док-во по сути верное, но автор пдфки сильно путается с верхним пределом интегрирования. Разбиение T у него на отрезке [a,b], а интегральная сумма почему-то стремится к интегралу по [a,t]; да и вообще непонятно, зачем давать подобную формулировку леммы, выделять какую-то t на [a,b], - это только с толку сбивает. Короткая формулировка: в собств. интеграле при равномерной сх-ти можно переходить к пределу под интегралом. Вот и сказал бы, что "положим на время док-ва, что интеграл по [a,b] собственный, а не несобственный..."
а когда и где в прошлом году распределяли заранее билеты?!
всем ботать, там не так много 

да теория ладно - главное какие задачи дадут
да теория ладно - главное какие задачи дадуттак вот и нехрен страдать про распределение билетов

Пара вопросов:
по рядам Фурье
1) Надо ли уметь доказывать теорему Фейера и условия равномерной сходимости ряда Фурье?
2) [тупняк]
утв. 1 - теорема Фейера. ("для любой непрерывной 2pi-периодической ф-и существует последовательность таких-то тригонометр. многочленов, равномерно сходящаяся к этой ф-и на всей области ее непрерывности и 2pi-периодичности").
утв. 2 - "частичная сумма степени n ряда Фурье функции f есть ее наилучшая в L_2-метрике аппроксимация тригонометрическими многочленами степени n".
вопрос: следует ли из этих 2 утверждений, что частичные суммы ряда Фурье равномерно приближают непрерывные 2pi-периодические функции?
[эти вопросы вообще возникли из вопроса о том, а какое приближение триг.многочленами степени n все-таки точнее - частичные суммы или суммы Фейера? (т.е. S_n или (S_1+S_2+S_3+...+S_n)/n?)]
по комплану
Надо ли уметь доказывать теорему единственности, принцип максимума, принцип открытости? Вообще что-то надо знать по голоморфным функциям?
апд: замечание к конспектам математиков по теме "поверхностные интегралы".
Кратко: ботать надо по чему-либо другому. Эта глава конспекта есть копипаст из Чубарикова-Архипова-Садовничего с выкидыванием некоторых фундаментальных определений и теорем (определение интеграла по поверхности, теорема о сведении интеграла по поверхности к двойному из-за чего она практически нечитабельна. Чтение по самому первоисточнику немногим лучше, так как в середине доказательства там всплывают слова (без предварительного определения) "инвариантность формы первого дифференциала", которые лично у меня вызывают тихий ужас. Явно ссылка на другую главу, но так делать нехорошо.
Замечательное док-во есть в Кудрявцеве, из него же заодно и становится понятно, зачем требовать второй, а не первый класс гладкости от r(u,v) (условие, неясно где прменяемое в док-ве из конспекта).
по рядам Фурье
1) Надо ли уметь доказывать теорему Фейера и условия равномерной сходимости ряда Фурье?
2) [тупняк]
утв. 1 - теорема Фейера. ("для любой непрерывной 2pi-периодической ф-и существует последовательность таких-то тригонометр. многочленов, равномерно сходящаяся к этой ф-и на всей области ее непрерывности и 2pi-периодичности").
утв. 2 - "частичная сумма степени n ряда Фурье функции f есть ее наилучшая в L_2-метрике аппроксимация тригонометрическими многочленами степени n".
вопрос: следует ли из этих 2 утверждений, что частичные суммы ряда Фурье равномерно приближают непрерывные 2pi-периодические функции?
[эти вопросы вообще возникли из вопроса о том, а какое приближение триг.многочленами степени n все-таки точнее - частичные суммы или суммы Фейера? (т.е. S_n или (S_1+S_2+S_3+...+S_n)/n?)]
по комплану
Надо ли уметь доказывать теорему единственности, принцип максимума, принцип открытости? Вообще что-то надо знать по голоморфным функциям?
апд: замечание к конспектам математиков по теме "поверхностные интегралы".
Кратко: ботать надо по чему-либо другому. Эта глава конспекта есть копипаст из Чубарикова-Архипова-Садовничего с выкидыванием некоторых фундаментальных определений и теорем (определение интеграла по поверхности, теорема о сведении интеграла по поверхности к двойному из-за чего она практически нечитабельна. Чтение по самому первоисточнику немногим лучше, так как в середине доказательства там всплывают слова (без предварительного определения) "инвариантность формы первого дифференциала", которые лично у меня вызывают тихий ужас. Явно ссылка на другую главу, но так делать нехорошо.
Замечательное док-во есть в Кудрявцеве, из него же заодно и становится понятно, зачем требовать второй, а не первый класс гладкости от r(u,v) (условие, неясно где прменяемое в док-ве из конспекта).
?
если заранее знаешь билет то можно сосредоточиться на задачах
если заранее знаешь билет то можно сосредоточиться на задачах
для механиков какие-нить материалы есть?
а ваще чо обычно с критериями - за что 4, за что 5?
+1
утв. 1 - теорема Фейера. ("для любой непрерывной 2pi-периодической ф-и существует последовательность таких-то тригонометр. многочленов, равномерно сходящаяся к этой ф-и на всей области ее непрерывности и 2pi-периодичности").Отет: не следует. Более того, частичные суммы ряда Фурье вовсе не обязаны сходиться (в каждой точке). С помощью теоремы Банаха-Штейнгауза легко доказывается, что существует непрерывная 2\pi-периодическая функция, ряд Фурье которой расходится в нуле (или в любой другой наперёд заданной точке).
утв. 2 - "частичная сумма степени n ряда Фурье функции f есть ее наилучшая в L_2-метрике аппроксимация тригонометрическими многочленами степени n".
вопрос: следует ли из этих 2 утверждений, что частичные суммы ряда Фурье равномерно приближают непрерывные 2pi-периодические функции?
На сколько билеты этого года отличаются от тех, что есть в шпорах с mexmat.net?
Сегодня на лекции по диффурам обнаружил разницу в 19 билете. Свежих у меня нет. Посмотрите кто-нибудь, плиз.
Сегодня на лекции по диффурам обнаружил разницу в 19 билете. Свежих у меня нет. Посмотрите кто-нибудь, плиз.
билет по конспектам местами нечитаем в принципе. В конспект входит теорема о продолжении, которой, во-первых, нет в программе, во-вторых, она нигде далее в билете не используется, и, в-третьих, она опять же вырвана с мясом из какой-то книги (без предварительного объяснения, что такое z(x; не понятно объяснение, почему решение не может выйти на границу и как это следует из леммы, и почему из невозможности выхода в свою очередь следует возможность продолжить его по временной оси. бред полный, в общем.
аналогичная проблема (конспект=тупой копипаст с дырками кстати, наблюдается во многих билетах конспекта.
два вот уже названы, и еще помню, что с проективкой то же самое.
аналогичная проблема (конспект=тупой копипаст с дырками кстати, наблюдается во многих билетах конспекта.
два вот уже названы, и еще помню, что с проективкой то же самое.
как там сегод госы? какие были задачи?
а какая разница
у всех групп же все по-разному
у всех групп же все по-разному
кафедра матана близка к кафедре функана по типам задач, след задачки могут быть подобные
кафедра матана близока к кафедре функана по типам задач, след задачки могут быть подобныефигня, каждый препод даст ту задачку, которую сам захочет дать
сдавали сеня госы
спрашивали часто комплан про вычеты (пощитать интеграл)
спрашивали часто комплан про вычеты (пощитать интеграл)
много задач задавали на человека?
какие критерии оценок?
какие критерии оценок?
много задач задавали на человека?
Как я понял, на разных кафедрах по-разному.
У нас (МАТИС) задавали помногу разнообразных задач на человека (мне 4 досталось но все они были очень простые, решались сходу
сейчас скажу условия, мож кому пригодятся.
апд:
1) Показать, что в теореме о почленном интегрировании степенного ряда существенно требование сильной, а не поточечной сходимости. Ответ: построение контрпримера, т.е. последовательности интегрируемых ф-й, которые сходятся лишь слабо, и интеграл от предельной функции не равен пределу интегралов f_n. Например, так: f_n = n, умноженный на индикатор отрезка [0,1/n]. Интегралы от f_n - единицы, слабый предел f_n - нуль, интеграл от него нуль.
2) Привести пример неабелевой группы. Когда я сказал S_3, попросили доказать, для док-ва достаточно проверить некоммутируемость перестановок (132) и (213 например. (это не циклы, а нижние строки таблицы перестановок с верхними строками 123).
3) Привести пример комплексного степенного ряда с центром в 0 и радиусом сх-ти 1, который на единичной окружности: а) сходится всюду б) расходится всюду в) где-то сходится и где-то расходится.
Пример распространенный, он есть в Шабате, ответ (а) - например, z^n делить на n в какой-нибудь степени, я сказал "миллион", но 2 там вполне достаточно. =) (б) z^n (в) z^n, деленное на n.
4) Даны 3 трехзначных числа, известно, что они делятся на 19, запишем их цифры в матрицу 3x3 (1 строка - 1 число). Верно ли, что ее det делится на 19?
Эту задачу я бы совсем простой не назвал, но после того как я минут 5 потупил и подумал, что надо вычитать строки и исследовать влияние этой операции на делимость det, нарисовал на доске переход методом Гаусса к ступенчатой матрице, пришел Галатенко, взглянул, говорит: "Ну да, мысль у вас правильная... дальше вы, наверное, знаете, как решать, так что ладно, идите". Туплю я сейчас сильно и как решение выглядит - знаю, но формализовать не могу, мозг отказывает, дорешайте кто-нибудь. =)
какие критерии оценок?
Рекомендованным в аспирантуру (внешнюю в т.ч. как я понял, ставили 5 довольно легко, но и к остальным не сказать, что прикапывались. Хотя это мб опять специфика МАТИС. Я с внешней рекомендацией, мне поставили 5 за билет + 3 решенные задачи + четвертая та самая, условно решенная. При этом простили неумение, как оказалось, интегрировать степенную ф-ю (прежде чем придумать индикаторы, раза 3 пытался построить гладкий контрпример - ряд вида "1 делить на x в степени", все 3 раза ошибался при взятии интеграла, потом плюнул. СЗМ, ага) и долгий тупняк в последней задаче (минут 5 стоял втыкал в доску, не написав ни слова). )
Троек по кафедре 4, четверок и пятерок примерно пополам.
Попал к халявному преподу.
Долго рассказывал и в итоге рассказал весь свой девятый билет.
Потом задали вопрос, что такое аналитическая функция, попросили привести как можно больше равносильных определений; добавили пару вопросов о гомоморфизме циклических групп. В конце дали некую "классическую задачу" : A*x = b, над Z2, вектора n-мерные, при каких условиях решаемо и если решаемо, то сколько решений.
Видел, как у соседа по доске спрашивали много примеров и контрпримеров на сходимость рядов и попросили привести пример функции, имеющей на [0;1] разрыв в каждой точке.
Также видел, как один чел без затупов и ошибок отвечал, вроде все нормально было, никаких претензий. Потом ему объявили четверку. На каком основании, почему - хз; вероятно сказалась поблажка на защите, когда немного дотянули оценку до 5.
Долго рассказывал и в итоге рассказал весь свой девятый билет.
Потом задали вопрос, что такое аналитическая функция, попросили привести как можно больше равносильных определений; добавили пару вопросов о гомоморфизме циклических групп. В конце дали некую "классическую задачу" : A*x = b, над Z2, вектора n-мерные, при каких условиях решаемо и если решаемо, то сколько решений.
Видел, как у соседа по доске спрашивали много примеров и контрпримеров на сходимость рядов и попросили привести пример функции, имеющей на [0;1] разрыв в каждой точке.
Также видел, как один чел без затупов и ошибок отвечал, вроде все нормально было, никаких претензий. Потом ему объявили четверку. На каком основании, почему - хз; вероятно сказалась поблажка на защите, когда немного дотянули оценку до 5.
А историю математики у кого-нить спрашивали? 

Даны 3 трехзначных числа, известно, что они делятся на 19, запишем их цифры в матрицу 3x3 (1 строка - 1 число). Верно ли, что ее det делится на 19?
Эту задачу я бы совсем простой не назвал, но после того как я минут 5 потупил и подумал, что надо вычитать строки и исследовать влияние этой операции на делимость det, нарисовал на доске переход методом Гаусса к ступенчатой матрице, пришел Галатенко, взглянул, говорит: "Ну да, мысль у вас правильная... дальше вы, наверное, знаете, как решать, так что ладно, идите". Туплю я сейчас сильно и как решение выглядит - знаю, но формализовать не могу, мозг отказывает, дорешайте кто-нибудь. =)
Над полем F_19 столбцы линейно зависимы => det = 0 (mod 19). => Делится. Если не туплю, конечно.
а чем случай Z2 отличается от всего остального?
Только возможными количествами решений.
вчера задали задачу посчитать сумму ряду:
1 + 1/2 - 1/3 - 1/4 + 1/5 + 1/6 - 1/7 - 1/8 + 1/9 + ...
1 + 1/2 - 1/3 - 1/4 + 1/5 + 1/6 - 1/7 - 1/8 + 1/9 + ...
Ответ: 1/2*ln2+pi/4, вроде бы.
Ряд логарифма \ln(1+x)=x-x^2/2+x^3/3-x^4/4+...
Ряд арктангенса \arctan(x)=x-x^3/3+x^5/5-...
Подставляем ln(1+1) и arctan(1) (ряды сходятся на (-1;1] и [-1;1] соответственно
Первый ряд делим пополам...
Задачка жесть - долго вспоминали, что это ряд арктангенса...
Ряд логарифма \ln(1+x)=x-x^2/2+x^3/3-x^4/4+...
Ряд арктангенса \arctan(x)=x-x^3/3+x^5/5-...
Подставляем ln(1+1) и arctan(1) (ряды сходятся на (-1;1] и [-1;1] соответственно
Первый ряд делим пополам...
Задачка жесть - долго вспоминали, что это ряд арктангенса...
решается легче:
рассмотрим такой ряд
f(x) = x + x^2/2 - x^3/3 - x^4/4 + x^5/5 + x^6/6 - x^7/7 - ...
тогда
f'(x) = 1 + x - x^2 - x^3 + x^4 + x^5 - x^6 - ... = (1 + x) / (1 + x^2)
отсюда f(x) = arctg(x) + 1/2 ln(1 + x^2)
а подставлять x = 1 имеем по второй теореме Абеля
ответ правильный
рассмотрим такой ряд
f(x) = x + x^2/2 - x^3/3 - x^4/4 + x^5/5 + x^6/6 - x^7/7 - ...
тогда
f'(x) = 1 + x - x^2 - x^3 + x^4 + x^5 - x^6 - ... = (1 + x) / (1 + x^2)
отсюда f(x) = arctg(x) + 1/2 ln(1 + x^2)
а подставлять x = 1 имеем по второй теореме Абеля

ответ правильный
А то какую задачу дают, зависит от билета или нет?
часто да.
и несколько, но первая по билету.
и несколько, но первая по билету.
Ответ-то правильный, только по какому праву вы решили переставить члены этих рядов в порядке через один? Ряд сходится условно, так что перестановка членов ряда незаконна.
на основании того, что ряд составленный из суммы К-ых элементов двух сходящихся рядов сходится к сумме сумм этих рядов
А, ну тогда ладно 

кстати, любимый ряд Седлецкого (1/ln(n) ) кому-нибудь давали? Кто знает решение?
Не знаю, давали ли его кому-нибудь (разве что чел ваще валился но решение до безобразия простое: раз (1/ln(n стремится к 0 при n стремящемся к бесконечности, то ряд, очевидно, сходится 

раз (1/ln(n стремится к 0 при n стремящемся к бесконечности, то ряд, очевидно, сходитсяда ну, правда?
а вот 1/n тоже к нулю стремится, а ряд вот чет не сходится
при этом ряд 1/(ln (n мажорирует указанный выше, поэтому расходится
Ну-ка кыш, всё сходится 

почему же?
Я чо-та не могу понять: у тебя в браузере картинки отключены или ты реально такой тупой? 

обычно отключаю, так грузится быстрее 

Не знаю, давали ли его кому-нибудь (разве что чел ваще валился но решение до безобразия простое: раз (1/ln(n стремится к 0 при n стремящемся к бесконечности, то ряд, очевидно, сходитсякрасивое решение

раз (1/ln(n стремится к 0 при n стремящемся к бесконечности, то ряд, очевидно, сходитсяЧто это за бред? Шутка юмора? или пропущено (-1)^n?
про ряд спрашивали на предыдущей странице
мне тоже кажется, что он знакочередующийся
однако на госах могут и не такую халяву решить дать
мне тоже кажется, что он знакочередующийся
однако на госах могут и не такую халяву решить дать
Что это за бред? Шутка юмора? или пропущено (-1)^n?
да хз, я пришел на лекцию почти последним, сел фигзнает где и не особо разглядел что он там написал
про мой ряд все очевидно, это неинтересно

а насчет когда (-1)^n не думал
тут, если я не ошибаюсь, как это ни странно подойдет решение Робина
вопрос к уже сдавшим:
(Основной вопрос) какая по вашему опыту(наблюдениям) наиболее оптимальная стратегия подготовки?
например, нужно ли хорошо разобраться во всех доквах или неточности могут сойти с рук?
нужно ли что б формулировки от зубов отлетали или по ним не гоняют?
на что лучше потратить время? (задачи, идеи док-в и тп.)
пс исправьте плиз слой
(Основной вопрос) какая по вашему опыту(наблюдениям) наиболее оптимальная стратегия подготовки?
например, нужно ли хорошо разобраться во всех доквах или неточности могут сойти с рук?
нужно ли что б формулировки от зубов отлетали или по ним не гоняют?
на что лучше потратить время? (задачи, идеи док-в и тп.)
пс исправьте плиз слой
на доске полные док-ва написать практически нереально, поэтому надо ботать, скорее, их идеи либо основной смысл
формулировки желательно хорошо знать, хотя тут все зависит от преподов. Некоторые дают только задачи, другие, напротив, спрашивают только условия теорем
Честно говоря, мне кажется, что многие принимающие не помнят всех доказательств экзамена и, быть может, особенностей формулировок. Так что неточности вполне могут сойти с рук, хотя тут тоже все зависит от принимающего.
Наверное, ботать нвдо только те вещи, которые написаны в билетах (скажем, не ботать неявных отображений, а только неявные функции). При этом, можно ботать их в более простых случаях, чем написано в конспектах с мехмат.нет. К билетам прилагается список литературы, из которого разумно выбрать самую простую книжку. например, в книжке Рашевского билеты по дифгему рассматриваются в случае R3, а не Rn, да и вообще, там все просто и понятно
формулировки желательно хорошо знать, хотя тут все зависит от преподов. Некоторые дают только задачи, другие, напротив, спрашивают только условия теорем
Честно говоря, мне кажется, что многие принимающие не помнят всех доказательств экзамена и, быть может, особенностей формулировок. Так что неточности вполне могут сойти с рук, хотя тут тоже все зависит от принимающего.
Наверное, ботать нвдо только те вещи, которые написаны в билетах (скажем, не ботать неявных отображений, а только неявные функции). При этом, можно ботать их в более простых случаях, чем написано в конспектах с мехмат.нет. К билетам прилагается список литературы, из которого разумно выбрать самую простую книжку. например, в книжке Рашевского билеты по дифгему рассматриваются в случае R3, а не Rn, да и вообще, там все просто и понятно
понял, спасибо
на доске полные док-ва написать практически нереально, поэтому надо ботать, скорее, ихя правильно понимаю, что сначала есть время чтобы выписать(списать) док-во на листок, а потом его основные идеи перенести на доску уже при ответе?
идеи либо основной смысл
да 

У меня два вопроса, которые, быть может, покажутся наивными...
1. Правда ли, что отвечать придётся только преподавателям со своей кафедры, как на защите диплома, или преподаватели с других кафедр тоже могут спрашивать?
2. Правда ли, что билеты будут разложены по номерам, или их перемешают, как на обычном экзамене?
1. Правда ли, что отвечать придётся только преподавателям со своей кафедры, как на защите диплома, или преподаватели с других кафедр тоже могут спрашивать?
2. Правда ли, что билеты будут разложены по номерам, или их перемешают, как на обычном экзамене?
да
2 мешают или нет зависит афаик от кафедры
лично я на это уже забил - мне пох какой билет выпадет
2 мешают или нет зависит афаик от кафедры
лично я на это уже забил - мне пох какой билет выпадет

Щас ботаю седлекции и возник вопрос по рядам Фурье.
Правда ли, что если f из C_2Pi и её ряд Фурье сх-ся, то сумма ряда совпадает с f?
В самих седлекциях зачем-то упоминается равномерная сх-сть, но накой она нужна? По теореме Фейера ведь все прекрасно получаетс.
Правда ли, что если f из C_2Pi и её ряд Фурье сх-ся, то сумма ряда совпадает с f?
В самих седлекциях зачем-то упоминается равномерная сх-сть, но накой она нужна? По теореме Фейера ведь все прекрасно получаетс.
более конструктивные вопросы:
(читаю , много думаю )
)
забыл комплан весь нах
1) объясните плиз про
как эта байда получается?
2) (вопрос всем и персонально Робину=)
как решается?
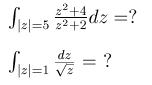
в первом там же вроде не 1го порядка полюс
кто помнит, как выглядит эта формула для полюса к-го порядка?
а про второй пример так дело и затухло вроде чему интеграл-то равен?
чему интеграл-то равен? 
(читаю , много думаю
 )
)забыл комплан весь нах

1) объясните плиз про
Задача: исследовать на особые очки функцию z/(sin(1/z^2
Ответы
0, +-sqrt(1/пи*k+-i*sqr(1/пи*kбесконечность
0 - не изолированная точка
бесконечность полюс 3го порядка
остальные полюса 1го порядка
как эта байда получается?
2) (вопрос всем и персонально Робину=)
как решается?
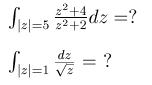
в первом там же вроде не 1го порядка полюс
Для того, чтобы посчитать интегралы типа первого, достаточно знать два факта.
1. Интеграл по замкнутому контуру Г функции f(z) равен сумме вычетов в особых точках z_i, лежащих внутри контура Г, умноженной на 2πi:
\int_Г f(z) dz = 2πi * \sum_i res_{z=z_i} f(z)
2. Вычет в полюсе первого порядка:
f(z) = g(z)/h(z g(a)≠0, a - нуль первого порядка для h, тогда res_{z=a} f(z) = g(a)/h'(a).
кто помнит, как выглядит эта формула для полюса к-го порядка?
а про второй пример так дело и затухло вроде
 чему интеграл-то равен?
чему интеграл-то равен? 
еще из форума осталось добить всего ничего =)
Кто знает решения?
1. Посчитать гл. кривизны и направления у z = x^2 - 9 y^2 в точке (0,0,0) - это потому что у меня билет был про это - 27.
2. тип сходимости на [0,1] (сходится ли, к чему сходится и как (равномерно или поточечно x - x^n при n\to\infty
3. тип сходимости на [0,1] x^n - x^{n+1}
4. (Говорят, такое спрашивают часто) решить y''(t) + y(t) = sin t - общий вид.
5. привести пример дифура с непрерывным полем скоростей, где есть существование, но нет единственности.
Кто знает решения?
кстати, еще оттуда же:
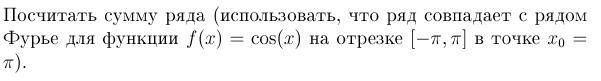
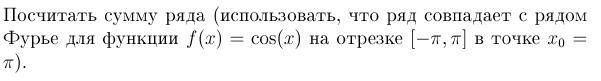
) Про z/(sin(1/z^2: особые точки — нули знаменателя, 0 и бесконечность, это понятно. Нули знаменателя такие, как там написано, при k стремящемся к бесконечности они все ближе подходят к 0, так что 0 — это точка накопления полюсов, т.е. не изолированная особая точка. В бесконечности рассматриваем g(z)=f(1/z)=1/(z*sin(z^2 sin(z^2)=z^2+...., так что g(z)=1/z^3+..., следовательно в бесконечности полюс третьего порядка.
) Интеграл номер 1. Здесь в +-2i полюс второго порядка. Но можно посчитать интеграл проще, чем искать в них вычеты: замечаем, что вне контура больше особых точек нет, кроме бесконечности, так что интеграл будет равен 2\pi*i, умножить на вычет в бесконечности, который считается так
res_\infty f(z) = - lim_{z->\infty} z(f(\infty)-f(z. Здесь f(\infty)=1, так что предел получается 0, а следовательно и интеграл равен 0.
Интеграл номер 2. Его проще всего считать, параметризуя окружность |z|=1 как z=e^{i\phi}, так что надо будет просто посчитать обычный интеграл по \phi от 0 до 2\pi.
res_\infty f(z) = - lim_{z->\infty} z(f(\infty)-f(z. Здесь f(\infty)=1, так что предел получается 0, а следовательно и интеграл равен 0.
Интеграл номер 2. Его проще всего считать, параметризуя окружность |z|=1 как z=e^{i\phi}, так что надо будет просто посчитать обычный интеграл по \phi от 0 до 2\pi.
Формула для вычета в полюсе k-го порядка:
res_{z_0} f(z) = 1/(k-1)! lim_{z\to z_0} z-z_0)^k f(z^{(k-1)}
(то, что в скобках под знаком предела, дифференцируется k-1 раз!)
Доказывается рассмотрением ряда Лорана в окрестности z_0.
res_{z_0} f(z) = 1/(k-1)! lim_{z\to z_0} z-z_0)^k f(z^{(k-1)}
(то, что в скобках под знаком предела, дифференцируется k-1 раз!)
Доказывается рассмотрением ряда Лорана в окрестности z_0.
2. тип сходимости на [0,1] (сходится ли, к чему сходится и как (равномерно или поточечно x - x^n при n\to\inftyПервая сходится поточечно, но не равномерно к 0 (близко к 1 посл-сть всегда будет принимать близкие к 1 значения). Вторая сходится равномерно: проверяется по определению, находишь максимум функции f_n(x)=x^n(1-x) на [0,1], он достигается в точке 1-1/n, а значение функции в этой точке стремится к 0 при n к бесконечности.
3. тип сходимости на [0,1] x^n - x^{n+1}
4. (Говорят, такое спрашивают часто) решить y''(t) + y(t) = sin t - общий вид.Общее решение ясно как находить, а частное надо искать в виде Asin(t)+Bcos(t подставляя в уравнение находим A и B (здесь будут оба равны -1/2).
1. Посчитать гл. кривизны и направления у z = x^2 - 9 y^2 в точке (0,0,0) - это потому что у меня билет был про это - 27Параметризуем r = r(u,v,u^2-9v^2) считаем
r_u = (1,0,2u)
r_v = (0,1,-18v)
r_uv=r_vu=0
r_uu=(0,0,2)
r_vv-(0,0,-18)
Первая форма G(0,0) = E (по определению считаем)
Нормаль n(0,0)=(0,0,1)
Вторая форма B = D(2, -18); det(B-\lamdaG)=0 => решения 2 и -18 и вектора (1,0) и (0,1)
Первая сходится поточечно, но не равномерно к 0 (близко к 1 посл-сть всегда будет принимать близкие к 1 значения). Вторая сходится равномерно: проверяется по определению, находишь максимум функции f_n(x)=x^n(1-x) на [0,1], он достигается в точке 1-1/n, а значение функции в этой точке стремится к 0 при n к бесконечности.Насчет второй. Сумма ряда в нуле и в единице 0, однако для других точек это будет
S(x^n(1-x = S(x^n1-x а сумма степеней на (0,1) будет 1/(1-x т.е. сумма ряда 1.
Т.е ряд непрерывных функций функций сходится к разрывной отсюда следует,
что нет равномерной непрерывности
так. я имею в виду ряды, а Робин похоже последовательности.
Как я понимаю что-то типа x'=|x|^(1/2) (x=x(t (Нарушается условие v_x непрерывна)
В окрестности точки (0,t_0) у нас в верхней полуплоскости будет
x = 0.25*(t-t_0)^2 (верхняя полуплоскость);
x = -0.25*(t+t_0)^2 (нижняя полуплоскость);
И x=0 решения, удовлетворяющие уравнению.
Все подходят под н.у.
5. привести пример дифура с непрерывным полем скоростей, где есть существование, но нет единственности.
Как я понимаю что-то типа x'=|x|^(1/2) (x=x(t (Нарушается условие v_x непрерывна)
В окрестности точки (0,t_0) у нас в верхней полуплоскости будет
x = 0.25*(t-t_0)^2 (верхняя полуплоскость);
x = -0.25*(t+t_0)^2 (нижняя полуплоскость);
И x=0 решения, удовлетворяющие уравнению.
Все подходят под н.у.
так. я имею в виду ряды, а Робин похоже последовательности.Да, я про последовательность. Неравномерная сходимость ряда из x^n - x^{n-1} следует непосредственно из неравномерной сходимости последовательности x^n.
спасибо!
скажем, не ботать неявных отображений, а только неявные функцииэто точно
когда препод у меня пытался спросить про неявные отображения, я ему честно сказал, что не знаю и знать не желаю
 - получил отл
- получил отлПри этом, можно ботать их в более простых случаях, чем написано в конспектах с мехмат.нетне можно, а нужно =)
ни у кого замечательной зеленой книжечки по дифурам (Филлипова) не завалялось случаем? =)
я бы зашел вечерком освежить в памяти как всякие извратские дифуры решаются
я бы зашел вечерком освежить в памяти как всякие извратские дифуры решаются

зеленой книжечки по дифурам (Филлипова)Она в сетке была когда-то.
Интеграл номер 1. Здесь в +-2i полюс второго порядка.
ты не опечатался? (+-i*sqrt(2 да и вообще первого порядка полюс имхо

Насчет sqrt(2) опечатался, а насчет второго порядка стормозил  первого, конечно.
первого, конечно.
 первого, конечно.
первого, конечно.замечаем, что вне контура больше особых точек нет, кроме бесконечности, так что интеграл будет равен 2\pi*i, умножить на вычет в бесконечности, который считается такres_\infty f(z) = - lim_{z->\infty} z(f(\infty)-f(z. Здесь f(\infty)=1, так что предел получается 0то ли опять опечатка, то ли я вообще первый раз вижу, чтобы так вычет на бесконечности считали (может, туплю).
ПС сам немого туплю, конструктив будет позже
может особая точка \infin устранима (lim=1) => res=0
неверно
неверно
может просто особая точка \infin устранима (lim=1) => res=0Если особая точка конечная и устранимая, то в ней вычет равен 0, но если она — бесконечность и устранимая, то не факт! Может быть и не 0! Пример: f(z)=1/z.
Так вычет считается, если $\infty$ является устранимой особенностью. При этом он вовсе не обязан равняться нулю (например, функция 1/z). То, что в данном случае вычет равен нулю, очевидно из тех соображений, что функция чётная.
P.S. Вообще-то, у нас в курсе комплана вычет на бесконечности определялся по-другому, поэтому интеграл равняется
минус 2\pi i умножить на вычет на бесконечности,
а вычет на бесконечности равняется минус коэффициенту при минус первой степени в ряде Лорана на бесконечности (т.е. никакого минуса в формуле Робина перед пределом не надо).
P.S. Вообще-то, у нас в курсе комплана вычет на бесконечности определялся по-другому, поэтому интеграл равняется
минус 2\pi i умножить на вычет на бесконечности,
а вычет на бесконечности равняется минус коэффициенту при минус первой степени в ряде Лорана на бесконечности (т.е. никакого минуса в формуле Робина перед пределом не надо).
вычет равен нулю, очевидно из тех соображений, что функция чётнаяО!
Ну там и вычеты считаются за минуту где-то

В данном примере, конечно, можно и вычеты посчитать. Но если дадут, например, интеграл по окружности |z|=5 от функции 1/(z^20-5)^10 (а было и такое то...
res_\infty f(z) = - lim_{z->\infty} z(f(\infty)-f(zзадача, конечно того не стоит, уже решена давно в лоб, но все-таки...
может тут так?
res_\infty f(z) = lim_{z->\infty} [f(zz-\infin)]
[f(zz-\infin)]Это из серии "невозможное возможно"?
который считается такможешь плиз объяснить почему?
res_\infty f(z) = - lim_{z->\infty} z(f(\infty)-f(z
В ответ на:
4. (Говорят, такое спрашивают часто) решить y''(t) + y(t) = sin t - общий вид.
Общее решение ясно как находить, а частное надо искать в виде Asin(t)+Bcos(t подставляя в уравнение находим A и B (здесь будут оба равны -1/2).
А ну ка подставь! Сколько раз в школе учили, что всегда надо подставлять ответ - все насмарку

йнах!
тибя апиридила кафедра матана 

фпитерке 

а как там дела с перемешиванием билетов?
там надо подставлять a*t*sint+b*t*cost
получиццо частное решение -0.5*t*sint
получиццо частное решение -0.5*t*sint
мы билеты не распределяли
пришел Арушанян и вывалил их на стол 

если кому интересно могу рассказать про задачку кот мне задал Староверов, довольно интересная
Мне интересно, выкладывай, че тебе этот  задал ?
задал ?
PS. Так ты ему сдавал?
 задал ?
задал ?PS. Так ты ему сдавал?

кажется он спросил, является ли файловая система СУБД
ред долго тупил, но решил правельно вроде
ред долго тупил, но решил правельно вроде
слышь ты, не  тут.
тут.
 тут.
тут.Потому что если бесконечность — устранимая особая точка, то ряд Лорана в ее окрестности имеет вид f(z) = c_0 + c_{-1}/z + ..., c_0 = f(\infty отсюда все следует (вычет в бесконечности равен -с_{-1}).
Согласен, налажал
и как такую задачу решать?
задачка такая:
пусть есть А и В - невырожденные матрицы
Вопрос: что можно сказать про невырожденность следующих матриц?
АВ (очевидно)
А+В (очевидно)
АА+ВВ
АА*+ВВ*
если кой-какие утверждения из линала подзабыть, то решать становится довольно прикольно=)
пусть есть А и В - невырожденные матрицы
Вопрос: что можно сказать про невырожденность следующих матриц?
АВ (очевидно)
А+В (очевидно)
АА+ВВ
АА*+ВВ*
если кой-какие утверждения из линала подзабыть, то решать становится довольно прикольно=)

wolf-cub
Здесь будем обсуждать до начала госов, как сдавать, что знать, что спрашивают из задач и т.д.