Примеры задач из экзамена мехмата МГУ (ГОСЭКЗАМЕН)
) S_3
)
А чёнть типа этого не пойдёт?
А чёнть типа этого не пойдёт?
) x^2 * функцию дирихле
спасибо! 
а эти:
3) привести пример несобственного интеграла, который нельзя интегрировать по параметру
4) привести пример ряда, у которого на окружности сходимости есть как точки в которых он сходится, так и точки в которых он расходится
а эти:3) привести пример несобственного интеграла, который нельзя интегрировать по параметру
4) привести пример ряда, у которого на окружности сходимости есть как точки в которых он сходится, так и точки в которых он расходится
). Таких рядов много. Например, ряд для ln (1 + x). Он сходится в точке x = 1 и, очевидно, расходится в точке x = -1.
) An = (X^n)/n. Радиус сходимости 1. В точке 1 расходится. В точке -1 сходится.
Откуда задачи берешь?
Откуда задачи берешь?
с миру по нитке...
А что такое S_3?
5) Привести пример оператора, все собств. значения которого равны 0.
5) Привести пример оператора, все собств. значения которого равны 0.
перестановки на трёх элементах.
5) матрица
0 1
0 0
5) матрица
0 1
0 0
А каков порядок у S_3, и почему он наименьший?
(1,2,3) , (2,3,1) -это разные элементы или нет?
(1,2,3) , (2,3,1) -это разные элементы или нет?
всё, что меньше - абелевы.
один и тот же.
один и тот же.
одинаковые?а можно тогда поподробней про S_3
)Пусть M- всюду плотное множество в R. Найти функцию f: f разрывна на M, и непрерывна на R/M
7)Обязан ли любой линейный оператор R^2 -> R^2 иметь одномерное инвариантное подпространство?
8)Числовой ряд сходится. Сходится ли ряд из а)квадратов б)кубов его членов?
Если не сложно, можно ли решения писать чуть подробней... Спасибо большое!
7)Обязан ли любой линейный оператор R^2 -> R^2 иметь одномерное инвариантное подпространство?
8)Числовой ряд сходится. Сходится ли ряд из а)квадратов б)кубов его членов?
Если не сложно, можно ли решения писать чуть подробней... Спасибо большое!
Для 1,2,3,4 я это сумел показать. А как для 5?
а какой порядок могут иметь элементы группы порядка 5? 
) нет
cos(phi) -sin(phi)
sin(phi) cos(phi)
cos(phi) -sin(phi)
sin(phi) cos(phi)
а поподробней, пожалуйста?
это матрица поворота плоскости на угол фи
и фи не кратен пи, если чо
а что такое инвариантное подпространство?
само в себя переходит
а №6,8?
и что значит плотное?
и что значит плотное?
Ступил. Я - то сидел случаи перебирал различных вариантов умножения и искал противоречия 
Для 1,2,3,4 получилось, а для 5 уже тяжеловато. Хотя еще за 10 минут я и с этим справился Решение целиком - листов на 5
Для 1,2,3,4 получилось, а для 5 уже тяжеловато. Хотя еще за 10 минут я и с этим справился Решение целиком - листов на 5 Теория на шпорах (для печати):
таблицы умножения выписывал?
) M - множество рациональных точек на R,
f(x)=0, если x - иррационально, и f=1/n, если х=m/n, где m/n - несократимая дробь
8) а) Не обязательно. Например: a_n=(-1)^n * n^(-1/2)
б) Не обязательно. Например: a_3n=n^(-1/3 a_{3n+1}=a_{3n+2}= -1/2 * n^(-1/3)
f(x)=0, если x - иррационально, и f=1/n, если х=m/n, где m/n - несократимая дробь
8) а) Не обязательно. Например: a_n=(-1)^n * n^(-1/2)
б) Не обязательно. Например: a_3n=n^(-1/3 a_{3n+1}=a_{3n+2}= -1/2 * n^(-1/3)
Ну грубо говоря да, только отметал сразу кучу очевидных случаев.
вообще не понимаю условие 7-0й задачи подпространство у оператора?
подпространство у оператора?Что за поверхность?
R^3. Берем плоскость в ней гипербола. Берем произвольную точку вне плоскости.
Соединяем отрезками точку и гиперболу получам поверхность. Что это за поверхность?
R^3. Берем плоскость в ней гипербола. Берем произвольную точку вне плоскости.
Соединяем отрезками точку и гиперболу получам поверхность. Что это за поверхность?
>Ну грубо говоря да, только отметал сразу кучу очевидных случаев.
например?
например?
Ну блин. Например для случая 4: e, a, b, c
Простейший пример a*b = a или b можно сразу отмести.
Простейший пример a*b = a или b можно сразу отмести.
) найти максимальный идеал в кольце непрерывных функций на отрезке. И напомните, пожалуйста, что такое идеал...
А эта задачка точно по программе?
PS: в программе нет колец, а следовательно и идеалов. только группы.
PS: в программе нет колец, а следовательно и идеалов. только группы.
когда-то кому-то задавали..
а 3-ю никто не знает..
и объясните, плззз, подробно задачу 1
а 3-ю никто не знает..
и объясните, плззз, подробно задачу 1
Вообще говоря на такие задачки сразу можно говорить что в программе такого не было. Это нормально. Препода иногда сами не очень знакомы с программой
вообще говоря, есть поле, а значит, и кольцо
Что значит нельзя интегрировать по параметру?
И что такое идеал?
И что такое идеал?
)
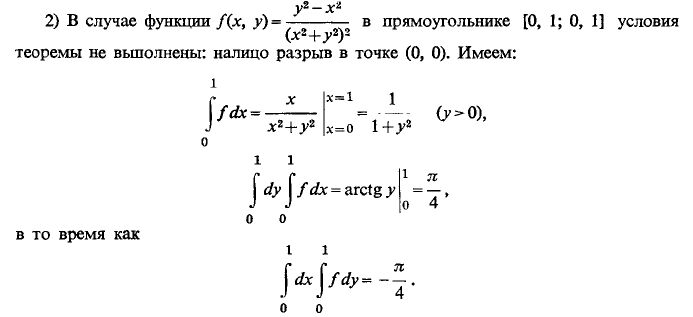
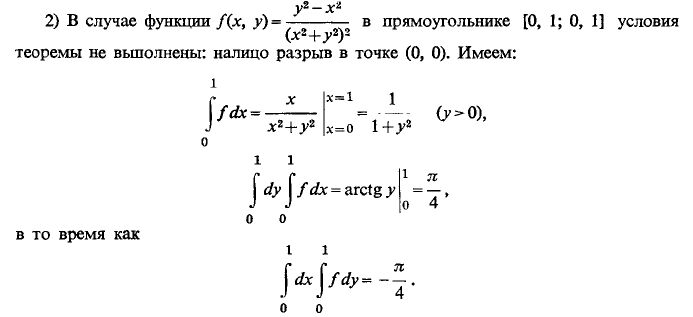
) про максимальный идеал непрерывных функций на отрезке
была такая задача на втором курсе, очень интересная и полезная
ответ там такой: это множество функций, обращающихся в 0 в фиксированной точке
сейчас напишу, примерно почему
была такая задача на втором курсе, очень интересная и полезная
ответ там такой: это множество функций, обращающихся в 0 в фиксированной точке
сейчас напишу, примерно почему
и еще , пожалуйста, напиши, что такое идеал кольца
Конуса часть.
Для определенности уравнение гиперболы xy=1, точка M=(0,0,1). Тогда уравнение прямых, проходящих через точки (a, 1/a) гиперболы и точку M, выглядит как x/a=ya=1-z. Выразив отсюда параметр a, получим уравнение конуса xy=(z-1)^2.
Для определенности уравнение гиперболы xy=1, точка M=(0,0,1). Тогда уравнение прямых, проходящих через точки (a, 1/a) гиперболы и точку M, выглядит как x/a=ya=1-z. Выразив отсюда параметр a, получим уравнение конуса xy=(z-1)^2.
)Д-ть, что функция возрастает вдоль grad F наиболее быстро
11)Имеется группа преобразований в R^3. Будет ли в ней подгруппа всех поворотов нормальной?
11)Имеется группа преобразований в R^3. Будет ли в ней подгруппа всех поворотов нормальной?
) значит так
то, что это идеал, проверяем по определению идеала
а то, что он максимальный, проверяем так: пусть не максимальный
тогда есть больший идеал (т.е. содержащий этот и еще какие-то функции (хотя бы одну
т.е. к множеству ВСЕХ функций, обращающихся в 0 в данной точке, присоединили функцию, которая НЕ обращается в 0 в этой точке
тогда возьмем и смастерим (сложением и умножением, в частности, возведением в квадрат) из имеющихся в большем идеале функций ТАКУЮ функцию, которая всюду на отрезке положительна И лежит в нашем большом идеале.
Тогда обратная к этой функции - тоже непрерывная. Перемножим их - произведение останется в идеале. Но идеал, содержащий 1, совпадает со всем кольцом и не является максимальным!
После обнаружения ЧИТАЮЩИМИ логического пробела в доказательстве напишу, что можно сделать, чтобы его не было
А теперь:
ОПРЕДЕЛЕНИЯ
идеала: идеал I в коммутативном кольце R --- это такая подгруппа по сложению I \subset R, что RI \subset I (т.е. умножение на элементы всего кольца не выводит за пределы идеала)
(в некоммутативном кольце есть понятия левостороннего, правостороннего и двустороннего идеалов; у нас кольцо коммутативное)
максимального идеала: идеал I \ne R в (коммутативном) кольце R максимальный, если
1) фактор-кольцо R/I --- поле
2) нет идеала J, отличного от всего R, такого что I содержится в J
условия равносильны
то, что это идеал, проверяем по определению идеала
а то, что он максимальный, проверяем так: пусть не максимальный
тогда есть больший идеал (т.е. содержащий этот и еще какие-то функции (хотя бы одну
т.е. к множеству ВСЕХ функций, обращающихся в 0 в данной точке, присоединили функцию, которая НЕ обращается в 0 в этой точке
тогда возьмем и смастерим (сложением и умножением, в частности, возведением в квадрат) из имеющихся в большем идеале функций ТАКУЮ функцию, которая всюду на отрезке положительна И лежит в нашем большом идеале.
Тогда обратная к этой функции - тоже непрерывная. Перемножим их - произведение останется в идеале. Но идеал, содержащий 1, совпадает со всем кольцом и не является максимальным!
После обнаружения ЧИТАЮЩИМИ логического пробела в доказательстве напишу, что можно сделать, чтобы его не было
А теперь:
ОПРЕДЕЛЕНИЯ
идеала: идеал I в коммутативном кольце R --- это такая подгруппа по сложению I \subset R, что RI \subset I (т.е. умножение на элементы всего кольца не выводит за пределы идеала)
(в некоммутативном кольце есть понятия левостороннего, правостороннего и двустороннего идеалов; у нас кольцо коммутативное)
максимального идеала: идеал I \ne R в (коммутативном) кольце R максимальный, если
1) фактор-кольцо R/I --- поле
2) нет идеала J, отличного от всего R, такого что I содержится в J
условия равносильны
Сильно покареженный конус получиться. Не конус, т.к. выбор точки произвольный. (То что эта точко бедет вершиной конуся сильно вряд ли)
) производная по направлению может быть посчитана как скалярное произведение градиента на направление (единичный вектор)
и когда же оно будет наибольшим, спрашивается.....
и когда же оно будет наибольшим, спрашивается.....
И сразу еще одна задача: построить касательную к окружности только с помощью линейки (центр окр. не дан).
)
) ответ отрицательный
берем ортогональную матрицу A
берем произвольную невырожденную матрицу B
верно ли, что C=BAB^{-1} обязательно ортогональная?
очевидно, нет: CC^t=BAB^{-1}\cdot B^{-1})^t)A^t B^t\ne E
можно для конкретики и строгости подобрать матрицы B и A
например: A=(0,1,0\\ -1,0,0\\ 0,0,1 B=(2,0,0\\ 0,1,0\\ 0,0,1)
тогда B^{-1}(B^{-1})^t = (1/4, 0,0\\ 0,1,0\\ 0,0,1)
A^t B^t = (0,-1,0\\ 2,0,0 \\ 0,0,1)
BA = (0,2,0\\ -1,0,0 \\ 0,0,1)
BA B^{-1}(B^{-1})^t = (0,2,0\\ -1/4,0,0 \\ 0,0,1)
в итоге CC^t = (4,0,0\\ 0,1/4,0\\ 0,0,1)
берем ортогональную матрицу A
берем произвольную невырожденную матрицу B
верно ли, что C=BAB^{-1} обязательно ортогональная?
очевидно, нет: CC^t=BAB^{-1}\cdot B^{-1})^t)A^t B^t\ne E
можно для конкретики и строгости подобрать матрицы B и A
например: A=(0,1,0\\ -1,0,0\\ 0,0,1 B=(2,0,0\\ 0,1,0\\ 0,0,1)
тогда B^{-1}(B^{-1})^t = (1/4, 0,0\\ 0,1,0\\ 0,0,1)
A^t B^t = (0,-1,0\\ 2,0,0 \\ 0,0,1)
BA = (0,2,0\\ -1,0,0 \\ 0,0,1)
BA B^{-1}(B^{-1})^t = (0,2,0\\ -1/4,0,0 \\ 0,0,1)
в итоге CC^t = (4,0,0\\ 0,1/4,0\\ 0,0,1)
Откуда цитатки?
Линейными преобразованиями пространства (поворот, растяжение и сдвиг) можно перевести любую гиперболу и точку вне плоскости гиперболы в описанную мной гиперболу и точку. При этих преобразованиях конус останется конусом. Я нигде не упоминал о вершине этого конуса.
ЗЫ: что такое покареженный конус?
ЗЫ: что такое покареженный конус?
из Фихтенгольца
Bosman: это подлая задача хотя средствами ангема решается.
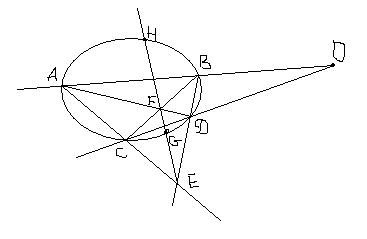
Дано: точка О и коника. Проводим две произвольных секущих ОА, ОС. Строим точки F и Е, проводим через них прямую, которая называется полярой точки О относительно коники. Она пересекает конику в точках касания, то есть OG и OH - это касательные.
Дано: точка О и коника. Проводим две произвольных секущих ОА, ОС. Строим точки F и Е, проводим через них прямую, которая называется полярой точки О относительно коники. Она пересекает конику в точках касания, то есть OG и OH - это касательные.
А доказать?
Во-во, еще бы доказал...
В ангеме стопудов это доказывалось. А сейчас ломает
отправляешь проективным преобразованием точку F в центр окружности и видишь, что AC и BD стали параллельны, значит, E ушла на бесконечность, значит, HG параллельно AC параллельно BD,
еще замечаешь, что AB параллельно CD, значит, O ушла на бесконечность, значит, прямые OH и OG параллельны AB и CD
и вообще ABDC прямоугольник, радиус FG по очевидным причинам уже перпендикуларен прамым OH и OG, значит, это касательные
еще замечаешь, что AB параллельно CD, значит, O ушла на бесконечность, значит, прямые OH и OG параллельны AB и CD
и вообще ABDC прямоугольник, радиус FG по очевидным причинам уже перпендикуларен прамым OH и OG, значит, это касательные
Чудеса
да, вот вам ещё порешать - чудо-вопрос от Винберга (в прошлом году было, внимание, я не опечатался):
существует ли абелева группа порядка 13?
существует ли абелева группа порядка 13?
Z_13 подойдёт? 
Клево! Видимо, надо было все-таки выучить проективную геометрию
Существует...
так с первого курса и не научился эллипс в гиперболу переводить?
эх, как мы тогда Панова
эх, как мы тогда Панова
Хех, ну я тогда тоже вспомню
Доказать, что если голоморфная в окрестности единичного круга функция обращается в ноль на некоторой дуге единичной окружности, то она тождественно равна нулю.
Доказать, что если голоморфная в окрестности единичного круга функция обращается в ноль на некоторой дуге единичной окружности, то она тождественно равна нулю.
Глупый вопрос(от меня): что такое характеристика поля?
Частный случай теоремы: если голоморфная в области функция обращается в ноль на множестве, принадлежащем данной области и имеющем предельную точку, то функция равна нулю во всей области.
Чуваааак, ты знааал
Именно этот момент я и вспомнил сегодня! До сих пор удивляюсь, за что тогда Тарас Евгеньевич мне пятерку поставил...
Собственно, задача к решающим: привести пример проективного преобразования, переводящего проективный эллипс в проективную гиперболу.
На первом курсе на экзамене я ее полтора часа решал
Именно этот момент я и вспомнил сегодня! До сих пор удивляюсь, за что тогда Тарас Евгеньевич мне пятерку поставил...
Собственно, задача к решающим: привести пример проективного преобразования, переводящего проективный эллипс в проективную гиперболу.
На первом курсе на экзамене я ее полтора часа решал
если 1+1+...+1=0 (p раз то p - характеристика поля. если такого нет, то 0.
кстати, сам-то так и не решил, что самое смешное
char F = min {n: 1+...+1 (n раз) = 0} или 0, если такого n не существует.
что такое ПРОЕКТИВНЫЙ эллипс и ПРОЕКТИВНАЯ гипербола?
овал и еще один овал?
овал и еще один овал?
а если б не я...
) Привести пример функционального ряда сходящегося, но не равномерно
ну да
Хотя и опередил, но написал не совсем точно
Надо ещё сказать, что такое p минимально, иначе подходят любые числа типа np, n натуральное.
Надо ещё сказать, что такое p минимально, иначе подходят любые числа типа np, n натуральное.
\sum_{n=0}^\infty (x^n - x^{n+1}) на [0,1]
Виноват, ступил. Условие такое:
Функция непрерывна в круге и голоморфна внутри круга. На границе круга обращается в ноль на некотором интервале. Доказать, что функция тождественно равна нулю.
Функция непрерывна в круге и голоморфна внутри круга. На границе круга обращается в ноль на некотором интервале. Доказать, что функция тождественно равна нулю.
один из фокусов отправить на бесконечность?
) решить sin(z)=2
Ну это совсем просто. Выпиши sin через e.
или можно провести любую касательную и отправить на бесконечность ее
Господа, на ГОСах задачи гораздо проще! Например, привести все коммутативные группы порядка 4.
По поводу:
Функция непрерывна в круге и голоморфна внутри круга. На границе круга обращается в ноль на некотором интервале. Доказать, что функция тождественно равна нулю.
А давайте чуть-чуть продолжим ее аналитически через этот интервал тождественным нулем
и тогда просто воспользуемся связностью полученной области
Функция непрерывна в круге и голоморфна внутри круга. На границе круга обращается в ноль на некотором интервале. Доказать, что функция тождественно равна нулю.
А давайте чуть-чуть продолжим ее аналитически через этот интервал тождественным нулем
и тогда просто воспользуемся связностью полученной области
а эти задачи тогда откуда?!
и как их привести?
Все группы порядка 4 коммутативны. Мне кажется этого достаточно.
Z_2*Z_2, кажись
Z_4 не забывайте
и вроде бы все тогда
и вроде бы все тогда
ну хз, шаллер тут говорит, что это от кафедры зависит. у них на вычмате спрашивали какие-то сложные задачи.
у нас - на первом потоке - все задачи были такие, что их можно было решить у доски за 2 минуты
а мне вообще Подольский на все задачи ответы сказал.
у нас - на первом потоке - все задачи были такие, что их можно было решить у доски за 2 минуты
а мне вообще Подольский на все задачи ответы сказал.
все, все
а, там наверное, как раз и было задание доказать, что все группы порядка 4 коммутативны
я наверное, торможу сильно.. но у меня чё-то нитакну,например, какие?
поясни
что ИМЕННО не так
что ИМЕННО не так
Кароче, синус = [e^iz-e^(-iz)]/2i
Заменяешь e^iz на t, получаешь квадратное уравнение
потом берешь логарифм от корней
Заменяешь e^iz на t, получаешь квадратное уравнение
потом берешь логарифм от корней
А кто сказал, что аналитическое продолжение существует?
Да, вот еще что надо сделать с условием этой задачи, чтобы оно стало полноценным =)
14) Функция непрерывна в круге и голоморфна внутри круга. На границе круга обращается в ноль на некотором интервале. Доказать, что функция тождественно равна нулю.
Да, вот еще что надо сделать с условием этой задачи, чтобы оно стало полноценным =)
14) Функция непрерывна в круге и голоморфна внутри круга. На границе круга обращается в ноль на некотором интервале. Доказать, что функция тождественно равна нулю.
ну там, исследовать на сходимость интеграл простенький
про группы всяких порядков любили спрашивать: 2, 4, 12 и тп
не помню я уже
про группы всяких порядков любили спрашивать: 2, 4, 12 и тп
не помню я уже
а это не простой принцип максимума?
Нет.
Принцип максимума: если функция голоморфна в области и непрерывна вплоть до границы, то она принимает максимальное значение на границе.
Но через него делается.
Принцип максимума: если функция голоморфна в области и непрерывна вплоть до границы, то она принимает максимальное значение на границе.
Но через него делается.
Имхо это бредятина. Что значит максимум для комплекснозначной функции?
Имеется в виду максимум модуля функции.
ты про бредятину насчёт принципа максимума на экзамене ещё скажи
продолжали же функции через границу области! причем существенно, чтобы был отрезок прямой или дуга окружности (одно в другое при необходимости переводится дробно-линейным)
доказывается для отрезка построением и проверкой
кажется, это именной принцип даже
!
где специалисты в такой момент?
доказывается для отрезка построением и проверкой
кажется, это именной принцип даже
!
где специалисты в такой момент?
Даже так! а про кусок ничего не сказано? т.е. необязательно, чтобы это был прямой кусок? как интересно... впрочем, логично, наверное...
впрочем, логично, наверное...минуточку!
если через него (принцип максимума) делается, то как использовать то, что она ноль на связном куске?
потому что иначе получается, что вообще в 0 обращаться не должна на границе круга!
если через него (принцип максимума) делается, то как использовать то, что она ноль на связном куске?
потому что иначе получается, что вообще в 0 обращаться не должна на границе круга!
это не Парамоновская книжка ли?
Да просто нужно применить "принцип минимума" - аналог принципа максимума, только для минимума модуля функции:
Голоморфная внутри области функция может достигать минимума модуля только на границе области, но не внутри неё.
Так что если где-то внутри круга (в точке z_0) функция не 0, то модуль |f(z_0)| тоже не 0 => противоречие с голоморфностью функции в силу теоремы выше.
Голоморфная внутри области функция может достигать минимума модуля только на границе области, но не внутри неё.
Так что если где-то внутри круга (в точке z_0) функция не 0, то модуль |f(z_0)| тоже не 0 => противоречие с голоморфностью функции в силу теоремы выше.
"Лаврентьев_Шабат - Методы теории функций комплексного переменного.djvu"
так. кто из нас тупой - ты или я?
смешно, конечно
что, голоморфные функции не имеют нулей?
что, голоморфные функции не имеют нулей?
я думала, что Мореру Морерой называет только Парамонов
Я
Не учёл, что в формулировке "принципа минимума" есть слова "... не может принимать минимума модуля, отличного от нуля, внутри области..."
Ну что же, тогда нужно копать в сторону доказательства, что f(z)=0 на всей границе круга (если хочется сделать через принцип максимума). Но это уже необязательно, раз уже доказали через аналитическое продолжение и теорему единственности
Не учёл, что в формулировке "принципа минимума" есть слова "... не может принимать минимума модуля, отличного от нуля, внутри области..."
Ну что же, тогда нужно копать в сторону доказательства, что f(z)=0 на всей границе круга (если хочется сделать через принцип максимума). Но это уже необязательно, раз уже доказали через аналитическое продолжение и теорему единственности
Долженко тоже называет Мореру Морерой
а задачи нерешенные остались или все обсудили уже?
по-моему, остались!
+ новая 15) Д-ть невозможность задания умножения над R^(2n+1) -линейное пространство нечетной размерности, n>0, так,ч тобы получилось поле
ну... это ответ истинного математика:
1) подумал
2) ответил правильно
3) пользы никакой
я не ориентируюсь во всех этих сообщениях, и не помню, чтобы что-то оставалось непонятное мне (хотя могло, кто ж меня знает)
"какие конкретно?" -- должен был звучать мой вопрос
1) подумал
2) ответил правильно
3) пользы никакой
я не ориентируюсь во всех этих сообщениях, и не помню, чтобы что-то оставалось непонятное мне (хотя могло, кто ж меня знает
)"какие конкретно?" -- должен был звучать мой вопрос
) посчитать для любого k (симметричная матрица в степени k)
2 3 ^k
3 2
2 3 ^k
3 2
Фтопку поля.
ну... если не очень сложно, то можно было бы поснить некоторые решения... хех... например, 7-ой задачи...
а еще было бы классно, если б кто-то доходчиво объяснил как вообще с этими группами разных порядков обращаться, как их искать и т.п.
а еще было бы классно, если б кто-то доходчиво объяснил как вообще с этими группами разных порядков обращаться, как их искать и т.п.
Теорема Мореры - официальное название, по-моему. В книжке Шабата оно есть. Наш лектор (Сергеев) его использовал.
это интересно
я так понимаю, умножение векторов на скаляры остается (т.е. нельзя ввести структуру АЛГЕБРЫ. чтобы она была полем)
примерно так:
от противного
берем элемент a, не пропорциональный вектору 1 (единица в нашем поле и фиксируем
все остальные умножаем на него
получаем линейный оператор (в поле есть аксиомы дистрибутивности и еще многие, поэтому он линейный)
но у него обязательно есть собственный вектор b (потому что есть собственное вещественное число, потому что многочлен (имеется в виду характеристический) нечетной степени имеет корень)
это значит, что ab=\lambda b
(a-\lambda \cdot 1) b =0
оба множителя не равны 0
в поле такого не бывает (есть обратные элементы)
я так понимаю, умножение векторов на скаляры остается (т.е. нельзя ввести структуру АЛГЕБРЫ. чтобы она была полем)
примерно так:
от противного
берем элемент a, не пропорциональный вектору 1 (единица в нашем поле и фиксируем
все остальные умножаем на него
получаем линейный оператор (в поле есть аксиомы дистрибутивности и еще многие, поэтому он линейный)
но у него обязательно есть собственный вектор b (потому что есть собственное вещественное число, потому что многочлен (имеется в виду характеристический) нечетной степени имеет корень)
это значит, что ab=\lambda b
(a-\lambda \cdot 1) b =0
оба множителя не равны 0
в поле такого не бывает (есть обратные элементы)
Да, по ходу, решение с аналитическим продолжением прокатывает.
Другое решение: если f(z) - та самая функция, заданная в единичном круге, и она равна нулю на дуге от 1 до exp(it то g(z)=f(z)*f(z*exp(-it равна нулю на дуге от 1 до exp(2it). Повторив эту операцию несколько раз, получим функцию h(z голоморфную в открытом круге и равную нулю на единичной окружности, к которой уже можно применить принцип максимума, h(z)=0 везде в круге. Теперь нужно найти внутри круга кучу точек, в которых f(z)=0, и воспользоваться теоремой единственности.
Другое решение: если f(z) - та самая функция, заданная в единичном круге, и она равна нулю на дуге от 1 до exp(it то g(z)=f(z)*f(z*exp(-it равна нулю на дуге от 1 до exp(2it). Повторив эту операцию несколько раз, получим функцию h(z голоморфную в открытом круге и равную нулю на единичной окружности, к которой уже можно применить принцип максимума, h(z)=0 везде в круге. Теперь нужно найти внутри круга кучу точек, в которых f(z)=0, и воспользоваться теоремой единственности.
а еще было бы классно, если б кто-то доходчиво объяснил как вообще с этими группами разных порядков обращаться, как их искать и т.п.Попробую.
Докажем, что все группы порядка меньше n=6 абелевы.
Для n = 1,2 очевидно.
Для n = 3 или 5: используем, что порядок элемента делит порядок группы. Так как 3 и 5 - простые числа, то существует элемент порядка, соответственно, 3 или 5. Тогда эта группа циклическая порядка соответственно 3 или 5, а значит, абелева.
Для n = 4. G = {e, a, b, c}. Вновь используем факт, что порядок элемента делит порядок группы. Порядки элементов в группе порядка 4 могут быть либо 2, либо 4 (других делителей у 4 нет). Если нашёлся элемент порядка 4, то это Z_4 - циклическая группа порядка 4, она абелева. Если такого элемента нет, то все элементы, кроме е, имеют порядок 2. Значит, a^2 = b^2 = c^2 = e. Докажем, что ab = c. Если это не так, например, ab = b, то домножаем справа на b^{-1}, и получаем, что a = e. Аналогично находим, что ba = c, ac = ca = b, bc = cb = a (отсюда видно, что группа абелева).
Итак, таблица умножения в нашей группе выглядит так:
| \ | e | a | b | c |
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
Это таблица умножения группы Z_2+Z_2.
3 ^k
3 2
=A
Это просто
А = C * I * C^-1
где I - жорданова матрица
В данном случае собств значения -1, 5
Собств вектора - (1,1 (1,-1)
Тогда С = ( ( 1, 1 ( 1, -1 ) C^-1 = ( ( 1/2, 1/2 ( 1/2, -1/2 ) )
I = ( ( 5, 0 ( 0, -1 ) )
A^n = C * I^n * C^-1
Дальше все очевидно
3 2
=A
Это просто
А = C * I * C^-1
где I - жорданова матрица
В данном случае собств значения -1, 5
Собств вектора - (1,1 (1,-1)
Тогда С = ( ( 1, 1 ( 1, -1 ) C^-1 = ( ( 1/2, 1/2 ( 1/2, -1/2 ) )
I = ( ( 5, 0 ( 0, -1 ) )
A^n = C * I^n * C^-1
Дальше все очевидно
PS: ответ:
( 5^n + (-1)^n ) / 2, ( 5^n - (-1)^n ) / 2
( 5^n - (-1)^n ) / 2, ( 5^n + (-1)^n ) / 2
( 5^n + (-1)^n ) / 2, ( 5^n - (-1)^n ) / 2
( 5^n - (-1)^n ) / 2, ( 5^n + (-1)^n ) / 2
А диагональная матрица тоже жорданова? 
да
наверное, ща глупость напишу (в упор не помню, что такое Жорданова форма):
верно ли что ЖФ - это диагональная матрица из собственных значений?
верно ли что матрица С - матрица из собственных векторов?
верно ли что ЖФ - это диагональная матрица из собственных значений?
верно ли что матрица С - матрица из собственных векторов?
Может я неправильно выразился? Мы приводим к жордановой форме. Матрица в отрыве от контекста ИМХО не может быть жордановой или не жордановой. Она жорданова только для определенной матрицы. И конечно, если все собств значения различны, то жорданова матрица - диагональна.
Верно, если все собственные значения различны.
Если среди них есть одинаковые, то неверно.
Если среди них есть одинаковые, то неверно.
Про C - да. Про I - не совсем.
там для кратных с.з. какие-то блоки надо писать, да?
ужас, как плохо, что семинары не писал
ужас, как плохо, что семинары не писал
Я не помню сам. Я просто перемножил. A = C * I * C^-1 => I = C * A * C^-1
Будем записывать матрицы так: (первая строчка; вторая строчка)
A = (2 3; 3 2) = 2Е + 3В, где Е - единичная матрица, В = (0 1; 1 0)
Можно использовать формулу бинома Ньютона, поскольку Е и В коммутируют друг с другом.
Учтем еще, что В*В = Е.
A^k = \sum_{m=0}^k C_k^m (3B)^m*(2A)^{k-m} =
= \sum_{m=0}^k 2^{k-m}*3^m*C_k^m * B^m = (a b; c d)
Легко видеть, что
a=d, b=c, a+b=(3+2)^k=5^k,
a-b = (2-3)^k = (-1)^k
Отсюда
A^k = ( (5^k+(-1)^k)/2 (5^k-(-1)^k)/2); (5^k+(-1)^k)/2 (5^k-(-1)^k)/2) )
A = (2 3; 3 2) = 2Е + 3В, где Е - единичная матрица, В = (0 1; 1 0)
Можно использовать формулу бинома Ньютона, поскольку Е и В коммутируют друг с другом.
Учтем еще, что В*В = Е.
A^k = \sum_{m=0}^k C_k^m (3B)^m*(2A)^{k-m} =
= \sum_{m=0}^k 2^{k-m}*3^m*C_k^m * B^m = (a b; c d)
Легко видеть, что
a=d, b=c, a+b=(3+2)^k=5^k,
a-b = (2-3)^k = (-1)^k
Отсюда
A^k = ( (5^k+(-1)^k)/2 (5^k-(-1)^k)/2); (5^k+(-1)^k)/2 (5^k-(-1)^k)/2) )
А точно легко видеть?
Запостить что ли ещё один способ, с использованием теоремы Гамильтона-Кэли?
О, сошлось.
Вот еще задача, на сообразительность (в смысле, имеется совсем тривиальное решение).
Рассмотрим матрицу А порядка n вот такого вида:
Вот еще задача, на сообразительность (в смысле, имеется совсем тривиальное решение).
Рассмотрим матрицу А порядка n вот такого вида:
Требуется возвести А в произвольную целую степень k.
0 1 0 0 ... 0 0
0 0 1 0 ... 0 0
0 0 0 1 ... 0 0
...
...
0 ... 0 1
1 0 0 ... 0
Ну типа легко, если выписать аккуратно то, что стоит в матрице, а потом попробовать это сложить и вычесть. Получатся как раз биномиальные формулы для
5^k = (2+3)^k
и
(-1)^k=(2-3)^k
5^k = (2+3)^k
и
(-1)^k=(2-3)^k
Довай. Заодно напомни теорему
Запость, интересно.
У меня только такая мысль: выписывать последовательно
A^2 - 4A - 5 = 0,
A^2 = 4A+5
A^3 = 4(4A+5) + 5A = 21A + 20
A^4 = 21(4A+5) + 20 A = ...
И так далее. Потом выписать и решить рекуррентные уравнения для коэффициентов.
У меня только такая мысль: выписывать последовательно
A^2 - 4A - 5 = 0,
A^2 = 4A+5
A^3 = 4(4A+5) + 5A = 21A + 20
A^4 = 21(4A+5) + 20 A = ...
И так далее. Потом выписать и решить рекуррентные уравнения для коэффициентов.
Ну это просто. Она циклически будет сдвигаться вправо.
) Пусть есть семейство подмножеств множества натуральных чисел со свойством: для любых двух множеств A и B из семейства либо A содержится в B, либо B содержится в A, либо A и B совпадают. Может ли семейство быть несчетным?
Или вверх
Ну это одно и то же
Фтопку. Теории множеств и логики нет в программе.
Не может.
Рассмотрим множества из этого семейства, имеющие ровно n элементов. Такое множество может быть только одно. Значит, вся система не более чем счетна.
Рассмотрим множества из этого семейства, имеющие ровно n элементов. Такое множество может быть только одно. Значит, вся система не более чем счетна.
Задача для своего решения требует только знания того, что такое счетное множество и что такое несчетное и когда-то давно предлагалась на госах
и чего?
ну, например, посчитаем для каждого множества сумму чисел в нем
получим ИНЪЕКТИВНОЕ отображение из нашего семейства в СЧЕТНОЕ множество натуральных чисел
значит, множеств в семействе не более, чем счетно
ну, например, посчитаем для каждого множества сумму чисел в нем
получим ИНЪЕКТИВНОЕ отображение из нашего семейства в СЧЕТНОЕ множество натуральных чисел
значит, множеств в семействе не более, чем счетно
Кто сказал, что множества конечны?
Я просто решил что если не смогу решить задачку, то буду утверждать что этого нет в программе Тренируюсь...мне стыдно 
Мне тоже
Итак, надо найти f(A где f(t) = t^n,
Характеристический многочлен матрицы А:
x_A(t) = (2-t)^2 - 9 = t^2 - 4t - 5 = (t - 5t + 1).
По теореме Гамильтона-Кэли, характеристический многочлен является аннулирующим для A: x_A(A) = 0. Поделим f(t) на x_A(t) с остатком:
f(t) = q(t) x_A(t) + p(t deg p <= 1,
f(A) = q(A) x_A(A) + p(A) = p(A
т.е. мы свели вычисление A^n к вычислению многочлена степени не больше 1 от А.
Пусть p(t) = at + b.
Имеем:
p(5) = 5a + b = 5^n
p(-1) = - a + b = (-1)^n
Отсюда находим a = (5^n - (-1)^n)/6, b = (5(-1)^n + 5^n)/6.
Значит,
A^n = (5^n - (-1)^n)/6 * А + (5(-1)^n + 5^n)/6 * E = ( (5^n + (-1)^n)/2, (5^n - (-1)^n)/2; (5^n - (-1)^n)/2, (5^n + (-1)^n)/2 ).
| ( | 2 | 3 | ) | |
| A = | ( | ) | ||
| ( | 3 | 2 | ) |
Характеристический многочлен матрицы А:
x_A(t) = (2-t)^2 - 9 = t^2 - 4t - 5 = (t - 5t + 1).
По теореме Гамильтона-Кэли, характеристический многочлен является аннулирующим для A: x_A(A) = 0. Поделим f(t) на x_A(t) с остатком:
f(t) = q(t) x_A(t) + p(t deg p <= 1,
f(A) = q(A) x_A(A) + p(A) = p(A
т.е. мы свели вычисление A^n к вычислению многочлена степени не больше 1 от А.
Пусть p(t) = at + b.
Имеем:
p(5) = 5a + b = 5^n
p(-1) = - a + b = (-1)^n
Отсюда находим a = (5^n - (-1)^n)/6, b = (5(-1)^n + 5^n)/6.
Значит,
A^n = (5^n - (-1)^n)/6 * А + (5(-1)^n + 5^n)/6 * E = ( (5^n + (-1)^n)/2, (5^n - (-1)^n)/2; (5^n - (-1)^n)/2, (5^n + (-1)^n)/2 ).
Заценил, красиво.
Мне тоже понравилось.
Блин, хорошая задачка. Пока что не дается.
Да ну, не дается.
Пример - сечения рациональных чисел действительными.
Пример - сечения рациональных чисел действительными.
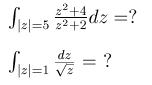
напомните пожалуйста как такие интегралы посчитать (через вычеты)
а заодно и
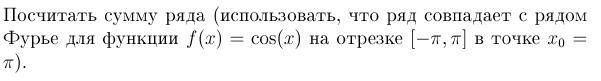
в прошлом году давали такие задачи.
как решить их?
17) Как связаны спектры матриц AB и BA (объяснить)
18) Какие возможные значения может принимать спектр вещественно кососимметрической матрицы 2n x 2n
19) пример функции такой, что её рад фурье сходится не к ней хотя бы в одной точке.
как решить их?
17) Как связаны спектры матриц AB и BA (объяснить)
18) Какие возможные значения может принимать спектр вещественно кососимметрической матрицы 2n x 2n
19) пример функции такой, что её рад фурье сходится не к ней хотя бы в одной точке.
Для того, чтобы посчитать интегралы типа первого, достаточно знать два факта.
1. Интеграл по замкнутому контуру Г функции f(z) равен сумме вычетов в особых точках z_i, лежащих внутри контура Г, умноженной на 2πi:
\int_Г f(z) dz = 2πi * \sum_i res_{z=z_i} f(z)
2. Вычет в полюсе первого порядка:
f(z) = g(z)/h(z g(a)≠0, a - нуль первого порядка для h, тогда res_{z=a} f(z) = g(a)/h'(a).
1. Интеграл по замкнутому контуру Г функции f(z) равен сумме вычетов в особых точках z_i, лежащих внутри контура Г, умноженной на 2πi:
\int_Г f(z) dz = 2πi * \sum_i res_{z=z_i} f(z)
2. Вычет в полюсе первого порядка:
f(z) = g(z)/h(z g(a)≠0, a - нуль первого порядка для h, тогда res_{z=a} f(z) = g(a)/h'(a).
а второй нельзя также посчитать?
там в нуле тоже полюс же
там в нуле тоже полюс же
Точно полюс? Что-то мне кажется, что там точка ветвления 1го порядка 
А точки ветвления вообще в программу госов не входят...
Макагня какая-то...
А точки ветвления вообще в программу госов не входят...
Макагня какая-то...
) Про спектры матриц AB и BA
Предлагаю такое объяснение:
det(AB-\lambda E)=det B det(AB-\lambda E) det B^{-1} =det (BA -\lambda E)
если B невырожденна
а если вырожденная, то можно найти B_n -> B, B_n невырождены
тогда det(AB_n-\lambda E) = det(B_nA -\lambda E
det(B_nA -\lambda E)-> det(BA-\lambda E)
det(AB_n-\lambda E)-> det(AB-\lambda E)
значит, всегда det(BA-\lambda E)=det(AB-\lambda E) (равенство многочленов)
спектры, соответственно, полностью совпадают
Предлагаю такое объяснение:
det(AB-\lambda E)=det B det(AB-\lambda E) det B^{-1} =det (BA -\lambda E)
если B невырожденна
а если вырожденная, то можно найти B_n -> B, B_n невырождены
тогда det(AB_n-\lambda E) = det(B_nA -\lambda E
det(B_nA -\lambda E)-> det(BA-\lambda E)
det(AB_n-\lambda E)-> det(AB-\lambda E)
значит, всегда det(BA-\lambda E)=det(AB-\lambda E) (равенство многочленов)
спектры, соответственно, полностью совпадают
что такое спектры?
Спектр оператора (матрицы) А - это множество комплексных чисел λ таких, что оператор A-λE необратим. В данном случае он только точечный, т.е. только такие λ, что det (A-λE) = 0.
да, там точка ветвления второго порядка.
В программу это как бы входит в разделе "многозначные функции"
может раскладывать в ряд Лорана и считать вычет в бесконечности (тоже особая точка)?
В программу это как бы входит в разделе "многозначные функции"
может раскладывать в ряд Лорана и считать вычет в бесконечности (тоже особая точка)?
Да блин, вопрос не в том, есть она или нет, вопрос в том, как склонять фамилию.
Дурацкий вопрос, где вы берете эти задачи? Решения-то придумать дело нехитрое, а вот сами задачи где взять?
Точно!
Тогда нужно просто интегрировать в другом направлении, появится знак "-":
\int_{|z|=1} 1/sqrt{z} dz = - 2πi * res_{z=∞} 1/sqrt{z}
А ∞ - устранимая особая точка для 1/sqrt{z}, поэтому вычет в ней равен 0, а значит и интеграл тоже 0.
Тогда нужно просто интегрировать в другом направлении, появится знак "-":
\int_{|z|=1} 1/sqrt{z} dz = - 2πi * res_{z=∞} 1/sqrt{z}
А ∞ - устранимая особая точка для 1/sqrt{z}, поэтому вычет в ней равен 0, а значит и интеграл тоже 0.
а то что корень - многозначная функция, это ничего?
Вроде ничего...
) Может ли у компактной поверхности быть гауссова кривизна всюду отрицательна?
нет
А почему хоть?
возьмём какую-нибудь координатную ось (глобальную). где-то вдоль нее проекция закончится, в соотв. точке поверхности седла быть не может ну никак.
блин, народ...
объясните мне что такое база и какое оперделение предела по базе
объясните мне что такое база и какое оперделение предела по базе
я так понимаю база по X (везде в билетах такая) - это x->x0, где x0 - предельная точка множества Х
напишите кто-нибудь как решать эти задачки
18) Какие возможные значения может принимать спектр вещественно кососимметрической матрицы 2n x 2n
19) пример функции такой, что её рад фурье сходится не к ней хотя бы в одной точке.
напишите кто-нибудь как решать эти задачки
18) Какие возможные значения может принимать спектр вещественно кососимметрической матрицы 2n x 2n
19) пример функции такой, что её рад фурье сходится не к ней хотя бы в одной точке.
База
1) Бесконечное множество подмножеств некоторого множества
2) Для любых А, B из базы в их пересечении есть элемент базы.
1) Бесконечное множество подмножеств некоторого множества
2) Для любых А, B из базы в их пересечении есть элемент базы.
) пример функции такой, что её рад фурье сходится не к ней хотя бы в одной точке.
Было. Берем функцию, рад Фурье для которой сходится к этой функции. А потом меняем значение функции в одной точке. Все интегралы(читай коэфф Фурье) не поменяются по свойствам интегралов.
Было. Берем функцию, рад Фурье для которой сходится к этой функции. А потом меняем значение функции в одной точке. Все интегралы(читай коэфф Фурье) не поменяются по свойствам интегралов.
а как определение предела по базе записывается:?
А как определить интеграл от многозначной функции по замкнутому контуру, обходящему точку ветвления?
Функция f(x) стремится к 0 (для примера) по базе, если для любого eps нейдется такой элемент базы, что на нем |f(x)|<eps
Сам не знаю, может кто-нибудь из рюхов подскажет?
Чубариков на консультации сказал, что про базы лучше вообще ничего не говорить, иначе сразу завалят
Да ладно. На какой кафедре завалят? И как говорить тогда?
передаю тока то, что говорил Чубариков
Я не думаю что на вычмате будут сильно придираться.
Может стоит отвечать на вопрос про такой интеграл так:
Интеграл от многозначной функции можно определить лишь на тех кривых, на которых мы можем выбрать однозначную ветвь, после указания на ветвь, которую мы будем интегрировать. Так как при обходе вдоль указанной в условии кривой мы переходим с одной ветви на другую, то интеграл не определен.
?
Кстати, вроде не верно, что бесконечность - устранимая особая точка, так как она является точкой ветвления, также как и 0 - не полюс. Вроде как понятие изолированных особых точек вводится только для однозначных функций.
Интеграл от многозначной функции можно определить лишь на тех кривых, на которых мы можем выбрать однозначную ветвь, после указания на ветвь, которую мы будем интегрировать. Так как при обходе вдоль указанной в условии кривой мы переходим с одной ветви на другую, то интеграл не определен.
?
Кстати, вроде не верно, что бесконечность - устранимая особая точка, так как она является точкой ветвления, также как и 0 - не полюс. Вроде как понятие изолированных особых точек вводится только для однозначных функций.
так всё-таки.
какие матрицы диагонализируются (все нужны) ?
какие матрицы диагонализируются (все нужны) ?
и ещё по матрицам пара вопросов.
что значит, когда определитель у матрицы ноль (вырожденная). что там с пространством собственных векторов?
(у жордановых форм, размерность пространства меньше размера матрицы. но определитель не ноль.)
что значит, когда определитель у матрицы ноль (вырожденная). что там с пространством собственных векторов?
(у жордановых форм, размерность пространства меньше размера матрицы. но определитель не ноль.)
Если определитель 0, то имеется непустое подпр-во, называемое ядром, которое матрица переводит в ноль. Размерность пр-ва = размер матрицы минус ранг матрицы. Все векторы из ядра будут собственными (отвечают собственному значению 0). Базис в ядре будет частью жорданова базиса для матрицы.
нихрена не понял
наверно завтра, когда протрезвею
неясно вото что. насколько помню, когда к жордановой приводили, определитель не равен был нулю (в тех матрицах, что нам давали) но размерность собственного пространства была меньше, т.е. есть ядро (размер матрицы минус размерность прост-ва собс-х векторов). или я чо-т не так понимаю?
наверно завтра, когда протрезвею
неясно вото что. насколько помню, когда к жордановой приводили, определитель не равен был нулю (в тех матрицах, что нам давали) но размерность собственного пространства была меньше, т.е. есть ядро (размер матрицы минус размерность прост-ва собс-х векторов). или я чо-т не так понимаю?
т.е. кароче у тебя получается, если не диагонализируема, то определитель ноль?
вопрос тогда про комплан:
ну выделила я в том интеграле ветвь, как дальше с ним бвть, как его считать?
ну выделила я в том интеграле ветвь, как дальше с ним бвть, как его считать?
Ну короче смотри. Есть матрица размера n. Ее ранг равен r. Тогда размерность ядра k=n-r.
Теперь пусть размерность пространства собственных векторов равна m. Совершенно не обязательно, чтобы m+k=n. То есть, бывают векторы, которые и не собственные, и не из ядра.
Пример:
(1 a)
(0 1)
n=2, r=2, k=0, m=1. Матрица уже приведена к жорд.форме, при этом первый вектор из текущего базиса собственный, а второй нет.
Получить диагональную матрицу в Жордановой форме можно, если m+k=n.
Теперь пусть размерность пространства собственных векторов равна m. Совершенно не обязательно, чтобы m+k=n. То есть, бывают векторы, которые и не собственные, и не из ядра.
Пример:
(1 a)
(0 1)
n=2, r=2, k=0, m=1. Матрица уже приведена к жорд.форме, при этом первый вектор из текущего базиса собственный, а второй нет.
Получить диагональную матрицу в Жордановой форме можно, если m+k=n.
> 18) Какие возможные значения может принимать спектр вещественно кососимметрической матрицы 2n x 2n
Смущает, что в моих рассуждениях не используется четность размера матрицы
Пусть A = -A' - косомимметрическая матрица, где ' - транспонирование.
Пусть t - собственное значение. Тогда |A-tE| = |A'-tE|=0, |(A-tE) (A'-tE)|=|(A-tE)| |(A'-tE) = 0, или |AA' + t^2E| = 0, т.е.
t - собственное значение А => -t^2 - собственное значение АА'. матрица АА' неотрицательно определена ( (AA'x, x) = (A'x, A'x) = |A'x|^2 >= 0 поэтому все собственные значения - вещественные неотрицательные числа (B>=0, Bx = sx, x \ne 0 => 0 <= (Bx, x) = (sx, x) = s(x, x) = s|x|^2, x \ne 0 => s >= 0 ).
Итак, t - собственное значение А => -t^2 >= 0.
Ответ. собственные числа матрицы А могут быть нулями и чисто мнимыми числами.
Наверно, я не понял, что значит вещественно кососимметричная
Смущает, что в моих рассуждениях не используется четность размера матрицы
Пусть A = -A' - косомимметрическая матрица, где ' - транспонирование.
Пусть t - собственное значение. Тогда |A-tE| = |A'-tE|=0, |(A-tE) (A'-tE)|=|(A-tE)| |(A'-tE) = 0, или |AA' + t^2E| = 0, т.е.
t - собственное значение А => -t^2 - собственное значение АА'. матрица АА' неотрицательно определена ( (AA'x, x) = (A'x, A'x) = |A'x|^2 >= 0 поэтому все собственные значения - вещественные неотрицательные числа (B>=0, Bx = sx, x \ne 0 => 0 <= (Bx, x) = (sx, x) = s(x, x) = s|x|^2, x \ne 0 => s >= 0 ).
Итак, t - собственное значение А => -t^2 >= 0.
Ответ. собственные числа матрицы А могут быть нулями и чисто мнимыми числами.
Наверно, я не понял, что значит вещественно кососимметричная
Да, ты прав, скорее всего.
Я ошибся, точка бесконечность для 1/sqrt{z} - тоже точка ветвления 1го порядка.
Только не верится что-то, что этот интеграл не определён ни в каком смысле...
P.S. Насчёт:
Если в окрестности особой точки многозначной функции при однократном обходе вокруг этой точки функция не переходит на другую ветвь, то это особая точка однозначного характера (для каждой ветви). Она может быть полюсом, устранимой или существенно особой, причём возможно, что на разных ветвях - разный тип особой точки
Например, f(z)=1/(1+sqrt{z}). Точки 0 и бесконечность - точки ветвления 1го порядка. А вот точка 1 - изолированная особая точка однозначного характера для f, т.к. при обходе точки 1 по достаточно малой окружности перехода на другую ветвь нет. Если g_0 - ветвь функции g(z)=sqrt{z}, соответствующая sqrt{1}=1, то на ветви f_0 = 1/(1+g_0) исходной функции f точка z=1 устранимая особая точка; если g_1 - ветвь g(z соответствующая sqrt{1}=-1, то на ветви f_1 = 1/(1+g_1) функции f точка z=1 - полюс первого порядка.
Я ошибся, точка бесконечность для 1/sqrt{z} - тоже точка ветвления 1го порядка.
Только не верится что-то, что этот интеграл не определён ни в каком смысле...
P.S. Насчёт:
Вроде как понятие изолированных особых точек вводится только для однозначных функций.Не совсем так, по-моему
Если в окрестности особой точки многозначной функции при однократном обходе вокруг этой точки функция не переходит на другую ветвь, то это особая точка однозначного характера (для каждой ветви). Она может быть полюсом, устранимой или существенно особой, причём возможно, что на разных ветвях - разный тип особой точки Например, f(z)=1/(1+sqrt{z}). Точки 0 и бесконечность - точки ветвления 1го порядка. А вот точка 1 - изолированная особая точка однозначного характера для f, т.к. при обходе точки 1 по достаточно малой окружности перехода на другую ветвь нет. Если g_0 - ветвь функции g(z)=sqrt{z}, соответствующая sqrt{1}=1, то на ветви f_0 = 1/(1+g_0) исходной функции f точка z=1 устранимая особая точка; если g_1 - ветвь g(z соответствующая sqrt{1}=-1, то на ветви f_1 = 1/(1+g_1) функции f точка z=1 - полюс первого порядка.
а как определение предела по базе записывается:?Пусть R - топологическое пространство, М - множество, B - база в M. Говорят, что точка p есть предел функции f:M->R по базе B, если прообраз всякой окрестности точки p при отображении f содержит некоторое окончание базы.
что такое базаМножество B некоторых непустых подмножеств множества M называется базой в М, а сами эти подмножества - окончаниями базы, если пересечение любых двух из них содержит некоторое окончание базы.
Пример базы в |R : x->a = {(a-eps,a+eps)\{a}:eps>0}
П.С. "Базис фильтра" - синоним слова "база". Фильтр - класс эквивалентных баз.
Любую ли матрицу можно привести к диагональному виду?
Нет
К диагональному виду можно привести только те матрицы, у которых все собственные значения различны.
не только такие
Есть две мазы:
1. Если все различны, то можно привести.
2. Если матрица симместрична, то можно привести.
Есть две мазы:
1. Если все различны, то можно привести.
2. Если матрица симместрична, то можно привести.
Разве нельзя привести такую матрицу?
(1 1)
(0 1)
(1 1)
(0 1)
А что ты вообще подразумеваешь под "привести"?
Элементарными преобразованиями можно привести, да: вычесть из первой строчки вторую.
А как линейный оператор в R^2 нельзя, это же жорданова клетка.
Элементарными преобразованиями можно привести, да: вычесть из первой строчки вторую.
А как линейный оператор в R^2 нельзя, это же жорданова клетка.
Пасиба
я думаю когда спросят про диагональный вид лучше не открывать рот про элементарные преобразования, могут и пару влепить
К диагональному виду можно привести только те матрицы, у которых все собственные значения различны.Контрпример
:(1 0)
(0 1)
можно привести, если размерность пространства собственных векторов совпадает с их количеством.
Извиняюсь, был неправ.
Ребята, СРОЧНО!
кто может доказать сходимость ряда 1/n?
очень надо!
кто может доказать сходимость ряда 1/n?
очень надо!
А что сложного-то?
1/n сходится к 0 при n->\inf, значит ряд сходится
1/n сходится к 0 при n->\inf, значит ряд сходится
Маза такая - 1/n^2 сходится к пи в квадрате делить на 6, значит 1/n к пи делить на корень из шести
Точно! Вот даже сумму посчитали.
А 1/sqrt{n} сходится к корень из пи, деленный на корень четвёртой степени из шести
А 1/sqrt{n} сходится к корень из пи, деленный на корень четвёртой степени из шести
Я тоже не понимаю, чего они так трудно дзета-функцию вычисляют, она же степенная....
Пиши статью в УМН
Революция в математике! Ура!
P.S. Ты меня в соавтарах там укажи, ок?
Революция в математике! Ура!
P.S. Ты меня в соавтарах там укажи, ок?
ещё задачка.
посчитать определитель матрицы 3х2
1 2 3
3 2 8
посчитать определитель матрицы 3х2
1 2 3
3 2 8
Продолжим матрицу естественным образом -
1 3 ---5
2 2 ---- 2
3 8 ------ 13
Задача свелась к определителю
1 2 3
3 2 8
5 2 13
Дальше сам....
1 3 ---5
2 2 ---- 2
3 8 ------ 13
Задача свелась к определителю
1 2 3
3 2 8
5 2 13
Дальше сам....
круто!
а то я думал дополню нулями и песдец определителю, абнулица
а то я думал дополню нулями и песдец определителю, абнулица
Я где-то встречал следующее доказательство :
Рассм. два ряда.
1) S'=a1+a2+a3+a4+...= 1 + 1/2 + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) +...
2) S''=b1+b2+b3+b4+...= 1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) +...
для любого i : ai>=bi
Для второго ряда имеем:
S''= 1 + 1/2 + 1/2 + 1/2 + ... -бесконечно раз суммируем число 1/2 => ряд 2) расх.=> 1) расх. по признаку сравнения.
:Рассм. два ряда.
1) S'=a1+a2+a3+a4+...= 1 + 1/2 + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) +...
2) S''=b1+b2+b3+b4+...= 1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) +...
для любого i : ai>=bi
Для второго ряда имеем:
S''= 1 + 1/2 + 1/2 + 1/2 + ... -бесконечно раз суммируем число 1/2 => ряд 2) расх.=> 1) расх. по признаку сравнения.
прикольненько
а как 1/2^n сумму пасчитать? тока на отрезке вспомнил, но это не док-во -
а как 1/2^n сумму пасчитать? тока на отрезке вспомнил, но это не док-во -
Этот ряд составлен из членов геом.прогресии.
Сумма n первых членов этого ряда как сумма n первых членов геом.пр. вычисляется по известной формуле
Sn=(a-a(q^n/(1-q
где a - первый член (=1/2 q-знаменатель прогрессии.
В данном случае q=1/2<1 => a(q^n)->0, при n->infty, следовательно,
lim_{n->infty}Sn = a/(1-q) = 1.
Сумма n первых членов этого ряда как сумма n первых членов геом.пр. вычисляется по известной формуле
Sn=(a-a(q^n/(1-q
где a - первый член (=1/2 q-знаменатель прогрессии.
В данном случае q=1/2<1 => a(q^n)->0, при n->infty, следовательно,
lim_{n->infty}Sn = a/(1-q) = 1.
ок. а как посчитать сумму 1/n^2?
(Pi^2)/6
считается через разложение sin в произведение, см. учебник комплана, например Маркушевич
считается через разложение sin в произведение, см. учебник комплана, например Маркушевич
R и C как группы по сложению - изоморфны или нет?
дайте определение поля
Кольцо без делителей нуля (т.е. в котором каждый ненулевой элемент обратим).
к тому же предполагается ассоциативность и коммутативность умножения
из обратимости всех ненулевых, конечно, следует отсутствие делителей нуля
из обратимости всех ненулевых, конечно, следует отсутствие делителей нуля
R и C как группы по сложению - изоморфны или нет?Что за звери такие вопросы на госах задают? Нет бы про ряд 1/n?
Ответ: да, при принятии AC. Решение такое: строим базисы Гаммеля b_1 - для R и b_2,b_3 для обеих компонент R в C=R+R . Потом говорим, что 2 континуума равны одному, и быстренько раскидываем базис b_1 по b_2, b_3.
Не люблю такие извращенные задачи
к тому же предполагается ассоциативность и коммутативность умноженияДа, забыл сказать, что кольцо коммутативное и ассоциативное. Правда, обычно это подразумевается...
если даже ассоциативность - и да, то про коммутативность кольца говорят отдельно
наверное, в учебнике по алгебраической геометрии подразумевается и то, и другое, в обычном учебнике алгебры - ассоциативность , а в учебнике, автор которого подвержен влиянию групп и алгебр Ли - ничего не подразумевается
наверное, в учебнике по алгебраической геометрии подразумевается и то, и другое
, в обычном учебнике алгебры - ассоциативность , а в учебнике, автор которого подвержен влиянию групп и алгебр Ли - ничего не подразумевается Кольцо без делителей нуля (т.е. в котором каждый ненулевой элемент обратим).Не понял из дальнейшего, обратили ли внимание что из 1-го не следует 2-е (кольцо целых чисел не имеет делителей нуля, но не является полем!).
ой, да, и это прозевал
то, о чем он говорит, в лучшем случае - область целостности (если еще единица есть там)
то, о чем он говорит, в лучшем случае - область целостности (если еще единица есть там)
Еще задачку вспомнил. Суть помню, а условие - не очень.
Бывают ли в R3 компактные гладкие поверхности (или поверхности без края, или и то, и другое, как-то так) всюду отрицательной кривизны.
Бывают ли в R3 компактные гладкие поверхности (или поверхности без края, или и то, и другое, как-то так) всюду отрицательной кривизны.
Боян
Было уже в этом треде и решение тоже было.
Было уже в этом треде и решение тоже было.
да, не пора ли оставить в треде вопросы и правильные ответы?
у кого когда госы то?
Точно баян
Нашел поиском на десятой странице этого треда
Нашел поиском на десятой странице этого треда
ggse3
кто-нибудь знает как решать:1) найти группу наименьшего порядка, которая не является коммутативной
2) пример функции, определенной на всей прямой, непрерывной лишь в одной точке и дифференцируемой в этой точке