Винеровский процесс в применении к ценам акций
Вообще-то, формула Блека-Шоулза предполагает, что цены подчиняются обобщенному винеровскому процессу ![[math]$dx=a\,dt+b\,dz$[/math]](mathimg.php?math=%24dx%3Da%5C%2Cdt%2Bb%5C%2Cdz%24) , где
, где ![[math]$dz$[/math]](mathimg.php?math=%24dz%24) - винеровский процесс с параметрами 0 и 1.
- винеровский процесс с параметрами 0 и 1.
Наверное, неявно предполагают, что если![[math]$h$[/math]](mathimg.php?math=%24h%24) - мало, то среднее
- мало, то среднее ![[math]$ah$[/math]](mathimg.php?math=%24ah%24) по порядку меньше волатильности (=стандартное отклонение)
по порядку меньше волатильности (=стандартное отклонение) ![[math]$\sigma\sqrt{h}$[/math]](mathimg.php?math=%24%5Csigma%5Csqrt%7Bh%7D%24) и им можно пренебречь
и им можно пренебречь
Наверное, неявно предполагают, что если
Для обобщённого винеровского процесса свойство приращений будет уже другим?
Под х подразумевается цена акции или её логарифм?
Под х подразумевается цена акции или её логарифм?
Здесь под ![[math]$x$[/math]](mathimg.php?math=%24x%24) подразумевается цена, т.е. если
подразумевается цена, т.е. если ![[math]$S_t$[/math]](mathimg.php?math=%24S_t%24) - цена в момент времени
- цена в момент времени ![[math]$t$[/math]](mathimg.php?math=%24t%24) , то бесконечно малое приращение
, то бесконечно малое приращение ![[math]$dS_t$[/math]](mathimg.php?math=%24dS_t%24) цены
цены ![[math]$S_t$[/math]](mathimg.php?math=%24S_t%24) за бесконечно малое время
за бесконечно малое время ![[math]$dt$[/math]](mathimg.php?math=%24dt%24) имеет вид
имеет вид ![[math]$dS_t=aS_t\,dt+\sigma S_t\,dz$[/math]](mathimg.php?math=%24dS_t%3DaS_t%5C%2Cdt%2B%5Csigma%20S_t%5C%2Cdz%24) .
.
В пределе при![[math]$h\to 0$[/math]](mathimg.php?math=%24h%5Cto%200%24) нормальность
нормальность ![[math]$\Delta_h \ln S_t :=\ln S_{t+h}-\ln S_t$[/math]](mathimg.php?math=%24%5CDelta_h%20%5Cln%20S_t%20%3A%3D%5Cln%20S_%7Bt%2Bh%7D-%5Cln%20S_t%24) и нормальность
и нормальность ![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) совпадают, ибо если обозначить через
совпадают, ибо если обозначить через ![[math]$\delta$[/math]](mathimg.php?math=%24%5Cdelta%24) отношение
отношение ![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) , то
, то
![[math]$$\ln S_{t+h}-\ln S_t = \ln \frac{S_t+S_{t+h}-S_t}{S_t}=\ln (1+\delta) = \delta - \frac{1}{2}\delta^2+=\ldots=\delta+o(\delta)$$[/math]](mathimg.php?math=%24%24%5Cln%20S_%7Bt%2Bh%7D-%5Cln%20S_t%20%3D%20%5Cln%20%5Cfrac%7BS_t%2BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%3D%5Cln%20%281%2B%5Cdelta%29%20%3D%20%5Cdelta%20-%20%5Cfrac%7B1%7D%7B2%7D%5Cdelta%5E2%2B%3D%5Cldots%3D%5Cdelta%2Bo%28%5Cdelta%29%24%24) .
.
Т.е. если![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) распределено нормально с параметрами
распределено нормально с параметрами ![[math]$a$[/math]](mathimg.php?math=%24a%24) и
и ![[math]$\sigma^2$[/math]](mathimg.php?math=%24%5Csigma%5E2%24) , то
, то ![[math]$\Delta_h \ln S_t$[/math]](mathimg.php?math=%24%5CDelta_h%20%5Cln%20S_t%24) распределено так же
распределено так же
В пределе при
Т.е. если
С винеровским процессом мне теперь всё понятно. Осталось только непонятным, почему нормальное распределение имеют не приращения процесса S_{t+h}-S_t, а приращения, делённые на S_t? Потому что это обобщённый винеровский процесс?
Если ![[math]$x$[/math]](mathimg.php?math=%24x%24) - стандартный винеровский процесс с параметрами 0 и 1, то обобщенный - это процесс
- стандартный винеровский процесс с параметрами 0 и 1, то обобщенный - это процесс ![[math]$z$[/math]](mathimg.php?math=%24z%24) для приращений которого
для приращений которого
![[math]$dz=a\,dt+b\,dx$[/math]](mathimg.php?math=%24dz%3Da%5C%2Cdt%2Bb%5C%2Cdx%24) и они независимы. Используя независимость, получаем, что за малое время
и они независимы. Используя независимость, получаем, что за малое время ![[math]$\delta t$[/math]](mathimg.php?math=%24%5Cdelta%20t%24) приращение
приращение ![[math]$\delta z=a\delta t + b\delta t$[/math]](mathimg.php?math=%24%5Cdelta%20z%3Da%5Cdelta%20t%20%2B%20b%5Cdelta%20t%24) имеет нормальное распределение со средним
имеет нормальное распределение со средним ![[math]$a\delta t$[/math]](mathimg.php?math=%24a%5Cdelta%20t%24) и дисперсией
и дисперсией ![[math]$b^2\delta t$[/math]](mathimg.php?math=%24b%5E2%5Cdelta%20t%24) .
.
Предполагается, что нормальность процентного изменения ![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) "более-менее" описывает поведение цены. А с точностью до малых большего порядка
"более-менее" описывает поведение цены. А с точностью до малых большего порядка ![[math]$\ln S_{t+h}-\ln S_t$[/math]](mathimg.php?math=%24%5Cln%20S_%7Bt%2Bh%7D-%5Cln%20S_t%24) и
и ![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) есть одно и то же
есть одно и то же
С логарифмами всё понятно  С обобщённым винеровским процессом - тоже. Только один вопрос остался: почему нормальное распределение имеют величины
С обобщённым винеровским процессом - тоже. Только один вопрос остался: почему нормальное распределение имеют величины 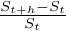 , ведь по свойствам винеровского процесса нормальное распределение имеет только числитель этой дроби?
, ведь по свойствам винеровского процесса нормальное распределение имеет только числитель этой дроби?
 С обобщённым винеровским процессом - тоже. Только один вопрос остался: почему нормальное распределение имеют величины
С обобщённым винеровским процессом - тоже. Только один вопрос остался: почему нормальное распределение имеют величины Ну да, но это ничего не даст для практики. Конечно, если рассмотреть фиксированный момент ![[math]$t$[/math]](mathimg.php?math=%24t%24) и цену
и цену ![[math]$S_t$[/math]](mathimg.php?math=%24S_t%24) , то малое приращение
, то малое приращение ![[math]$\delta S_t=S_{t+h}-S_t$[/math]](mathimg.php?math=%24%5Cdelta%20S_t%3DS_%7Bt%2Bh%7D-S_t%24) имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами ![[math]$aS_t\delta t$[/math]](mathimg.php?math=%24aS_t%5Cdelta%20t%24) и
и ![[math]$b^2S_t^2\delta t$[/math]](mathimg.php?math=%24b%5E2S_t%5E2%5Cdelta%20t%24) , но все это при малом
, но все это при малом ![[math]$h$[/math]](mathimg.php?math=%24h%24) и больше этого в принципе ничего не получается, но если взять процентное изменение
и больше этого в принципе ничего не получается, но если взять процентное изменение ![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) вместо обычного приращения
вместо обычного приращения ![[math]$S_{t+h}-S_t$[/math]](mathimg.php?math=%24S_%7Bt%2Bh%7D-S_t%24) (то есть от цен акций переходить к доходностям то за малое время
(то есть от цен акций переходить к доходностям то за малое время ![[math]$\delta t$[/math]](mathimg.php?math=%24%5Cdelta%20t%24) процентное изменение
процентное изменение ![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) имеет распределение с параметрами
имеет распределение с параметрами ![[math]$a\delta t$[/math]](mathimg.php?math=%24a%5Cdelta%20t%24) и
и ![[math]$b^2\delta t$[/math]](mathimg.php?math=%24b%5E2%5Cdelta%20t%24)
В чем суть? Распределение![[math]$\frac{S_{t+h}-S_t}{S_t}$[/math]](mathimg.php?math=%24%5Cfrac%7BS_%7Bt%2Bh%7D-S_t%7D%7BS_t%7D%24) - стационарно (при предположениях, что волатильность (=стандартное отклонение) не меняется со временем (хотя это неверно, но для лекций этого достаточно
- стационарно (при предположениях, что волатильность (=стандартное отклонение) не меняется со временем (хотя это неверно, но для лекций этого достаточно  ) и снос
) и снос ![[math]$a$[/math]](mathimg.php?math=%24a%24) не меняется со временем) - т.е. распределение не меняется со временем.
не меняется со временем) - т.е. распределение не меняется со временем.
Если же взять![[math]$S_{t+h}-S_t$[/math]](mathimg.php?math=%24S_%7Bt%2Bh%7D-S_t%24) , то у него получается нормальность с параметрами
, то у него получается нормальность с параметрами ![[math]$aS_t\delta t$[/math]](mathimg.php?math=%24aS_t%5Cdelta%20t%24) и
и ![[math]$b^2S_t^2\delta t$[/math]](mathimg.php?math=%24b%5E2S_t%5E2%5Cdelta%20t%24) - меняется с изменением цены
- меняется с изменением цены
В чем суть? Распределение
 ) и снос
) и снос Если же взять
У меня были ошибочные представления о винеровском процессе, значит. 
То есть если у нас есть обобщённый винеровский процесс с параметрами a и b, то при известном состоянии
с параметрами a и b, то при известном состоянии  в момент t имеется в виду условное распределение, которое будет иметь параметры не 0 и
в момент t имеется в виду условное распределение, которое будет иметь параметры не 0 и  , не
, не 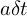 и
и 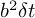 , а именно
, а именно 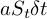 и
и 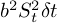 ?
?

То есть если у нас есть обобщённый винеровский процесс
Чё-то я не понял смысл вопроса..
Мне не очень понятно, почему в параметры нормального распределения приращений S_{t+h}-S_t влезло S_t... То, что у стандартного винеровского процесса параметры будут 0 и h это ясно, мне непонятно, почему у обобщённого они умножаются не просто на a и b, а ещё и на S_t.
Потому что мы постулируем: ![[math]$dS_t=aS_t\,dt + \sigma S_t\,dz$[/math]](mathimg.php?math=%24dS_t%3DaS_t%5C%2Cdt%20%2B%20%5Csigma%20S_t%5C%2Cdz%24) ,
, ![[math]$a,\ b$[/math]](mathimg.php?math=%24a%2C%5C%20b%24) - постоянные,
- постоянные, ![[math]$S_t$[/math]](mathimg.php?math=%24S_t%24) - фиксировано в моменте. Это означает, что
- фиксировано в моменте. Это означает, что ![[math]$S_{t+\delta t}-S_t=aS_t\delta t+\sigma S_t\delta z$[/math]](mathimg.php?math=%24S_%7Bt%2B%5Cdelta%20t%7D-S_t%3DaS_t%5Cdelta%20t%2B%5Csigma%20S_t%5Cdelta%20z%24) (при
(при ![[math]$\delta t\to 0$[/math]](mathimg.php?math=%24%5Cdelta%20t%5Cto%200%24) . Так как
. Так как ![[math]$\delta z \sim N(0, \delta t)$[/math]](mathimg.php?math=%24%5Cdelta%20z%20%5Csim%20N%280%2C%20%5Cdelta%20t%29%24) , то
, то ![[math]$S_{t+\delta t}-S_t\sim N(aS_t\delta t, \sigma^2S_t^2\delta t)$[/math]](mathimg.php?math=%24S_%7Bt%2B%5Cdelta%20t%7D-S_t%5Csim%20N%28aS_t%5Cdelta%20t%2C%20%5Csigma%5E2S_t%5E2%5Cdelta%20t%29%24)
То есть здесь 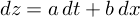 (как ты пишешь в одном из первых постов) а и сигма - на самом деле не константы, а линейные функции S_t?
(как ты пишешь в одном из первых постов) а и сигма - на самом деле не константы, а линейные функции S_t?
Я искренне извиняюсь, я напутал. Моя вина 
Если![[math]$z$[/math]](mathimg.php?math=%24z%24) - винеровский процесс с параметрами
- винеровский процесс с параметрами ![[math]$a$[/math]](mathimg.php?math=%24a%24) и
и ![[math]$b^2$[/math]](mathimg.php?math=%24b%5E2%24) , то
, то ![[math]$dz=a\,dt+b\,dx$[/math]](mathimg.php?math=%24dz%3Da%5C%2Cdt%2Bb%5C%2Cdx%24) , где
, где ![[math]$x$[/math]](mathimg.php?math=%24x%24) - стандартный винеровский процесс с параметрами 0 и 1. И плюс, в винеровском процессе предполагается, что
- стандартный винеровский процесс с параметрами 0 и 1. И плюс, в винеровском процессе предполагается, что ![[math]$a,b$[/math]](mathimg.php?math=%24a%2Cb%24) - константы.
- константы.
Если![[math]$a$[/math]](mathimg.php?math=%24a%24) и
и ![[math]$b$[/math]](mathimg.php?math=%24b%24) - есть функции от
- есть функции от ![[math]$S_t$[/math]](mathimg.php?math=%24S_t%24) и
и ![[math]$t$[/math]](mathimg.php?math=%24t%24) - то это уже не винеровский процесс! Это называется процессом Ито.
- то это уже не винеровский процесс! Это называется процессом Ито.
Так что исправляюсь: цена ведет себя как процесс Ито, а процентное изменение - как обобщенный винеровский процесс.

Если
Если
Так что исправляюсь: цена ведет себя как процесс Ито, а процентное изменение - как обобщенный винеровский процесс.
Огромное спасибо!  Всё понятно теперь!
Всё понятно теперь!
 Всё понятно теперь!
Всё понятно теперь!
yurkuz
Применительно к модели Блэка-Шоулса: если мы рассматриваем приращения винеровского процесса за время h, то следующие величины - приращения процессаимеют нормальное распределение с математическим ожиданием ah и дисперсией сигма в квадрате, умноженная на h.
Как же так? Ведь приращения винеровского процесса имеют нулевое среднее!
Если у нас есть винеровский процесс W(t то W(t)-W(s) имеет нормальное распределение с параметрами 0 и t-s. Насчёт дисперсии понятно, можно просто нормировать, разделив приращения на сигма. Но куда деть матожидание? Что в модели Блэка-Шоулса в действительности является винеровским процессом?