Является ли окружность эллипсом
Кстати, я тут подразобрался в вопросе. И с математической точки зрения круг - не эллипс. У эллипса есть ровно две оси симметрии, а у круга - бесконечное количество.Дайка мне определение эллипса.
возьмика в интернете
а то я могу напутать. Но по памяти так:
эллипс - геометрическое место точек: сумма расстояний от каждой из них до двух заданных (называемых фокусами) одна и та же.
А вот окружность. Геометрическое место точек: расстояние от каждой из них до одной заданной (называемой центром) одно и то же.
Казалось бы можно совершить предельный переход и совместить две точки-фокусы. Но именно наличие двух осей симметрии у эллипса и бесконечного числа осей симметрии у окружности показывает, что этот переход не совсем гладкий. Что эти два объекта по этому признаку отличаются принципиально.
а то я могу напутать. Но по памяти так:
эллипс - геометрическое место точек: сумма расстояний от каждой из них до двух заданных (называемых фокусами) одна и та же.
А вот окружность. Геометрическое место точек: расстояние от каждой из них до одной заданной (называемой центром) одно и то же.
Казалось бы можно совершить предельный переход и совместить две точки-фокусы. Но именно наличие двух осей симметрии у эллипса и бесконечного числа осей симметрии у окружности показывает, что этот переход не совсем гладкий. Что эти два объекта по этому признаку отличаются принципиально.
эллипс - геометрическое место точек: сумма расстояний от каждой из них до двух заданных (называемых фокусами) одна и та же.Ага, и нигде не говорится что эти точки не могут совпадать.
но 2 не равно 1, вроде и так очевидно. Потому не упоминают.
но 2 не равно 1, вроде и так очевидно. Потому не упоминают.У тебя проблемы с логикой видимо. В любом случае, не поленился загуглить и во всех встретившихся определениях упоминается, что круг частный случай эллипса.
там же наверно какие-то тривиальные "грубые" определения.
А если посмотреть с позиции серьезной науки, то эллипс это круг со спонтанно нарушенной симметрией:
SO(2)->O(1)*O(1)
А если посмотреть с позиции серьезной науки, то эллипс это круг со спонтанно нарушенной симметрией:
SO(2)->O(1)*O(1)
С позиции серьезной науки круг это не эллипс и даже не окружность. А окружность это эллипс.
Ты опять пытаешься отсутствие элементарных знаний скрыть более навороченными, которые тут вообще ни при чем? Выглядит смешно.
Ты опять пытаешься отсутствие элементарных знаний скрыть более навороченными, которые тут вообще ни при чем? Выглядит смешно.
> С позиции серьезной науки
А что такое "серьёзная наука"? Математика, что ли?
Так она и не наука.
В целом, группа симметрии гораздо важнее глупого математического свойства.
---
"Математик может говорить, что ему хочется,
но физик должен, хотя бы в какой-то мере, быть в здравом рассудке."
А что такое "серьёзная наука"? Математика, что ли?
Так она и не наука.
В целом, группа симметрии гораздо важнее глупого математического свойства.
---
"Математик может говорить, что ему хочется,
но физик должен, хотя бы в какой-то мере, быть в здравом рассудке."
я тут борюсь против ссылок на незыблемые авторитеты "серьезной науки". Потому что получается, что мы тут - так, детишки в песочнице. А вот есть некие серьезные дяди, которые говорят как "правильно", и мы должны их слушаться.
Между тем, мы - это форум МГУшников. А это - раздел Стади, в котором мы вполне можем и должны творить науку, а не молиться на нее, боясь святотатственно поколебать какие-то там "устоявшиеся" определения эллипса и окружности.
Между тем, мы - это форум МГУшников. А это - раздел Стади, в котором мы вполне можем и должны творить науку, а не молиться на нее, боясь святотатственно поколебать какие-то там "устоявшиеся" определения эллипса и окружности.
Что-же ты тогда ромб эллипсом не называешь, группа симметрий то та же?
Если тебе не нравится общепринятая терминология, то это твои личные проблемы.
Если тебе не нравится общепринятая терминология, то это твои личные проблемы.
Вот допустим наблюдаются некие процессы. В одном случае у процесса всего лишь две оси симметрии, а в другом - круговая симметрия. И что, так легко утверждается, что это одно и то же? Так нельзя.
Математика это язык. Если в некоем языке синий=blue и голубой=blue, то на этом языке нельзя передать определенные нюансы, связанные с цветом. Если выражать процесс математически как эллипс, и рассматривать окружность как частный случай эллипса, то есть риск потерять по пути важные нюансы, связанные с симметриями этого процесса.
Математика это язык. Если в некоем языке синий=blue и голубой=blue, то на этом языке нельзя передать определенные нюансы, связанные с цветом. Если выражать процесс математически как эллипс, и рассматривать окружность как частный случай эллипса, то есть риск потерять по пути важные нюансы, связанные с симметриями этого процесса.
Так она и не наука.А ТЫ - ХУЙ!
И с математической точки зрения круг - не эллипс. У эллипса есть ровно две оси симметрии, а у круга - бесконечное количество. По этому признаку они и различаются. Ибо нет гладкого перехода от 2 к бесконечности.с математической точки зрения квадрат - не прямоугольник. у прямоугольника 2 оси симметрии, а у квадрата - 4. по этому признаку они и различаются. ибо нет гладкого перехода от 2 к 4.
что круг частный случай эллипса.окружность - это вырожденный случай эллипса.
ps
прав: понятия что в "быту", что в науке - вводятся не абы как, а вводятся так, чтобы обозначать определенный набор объектов(явлений обладающими одними и теми же свойствами.
утверждение "A является частным случаем B" означает, что для A выполняются свойства B.
утверждение "A является вырожденным случаем B" означает, что при переводе B в A происходит предельный переход и часть свойств B у объекта A уже не наблюдается (скачкоообразо меняется).
pps
Дальше это вопрос определений терминов.
Если для термина эллипс фиксируется, что эллипс обладает свойством (следствием что он имеет две оси симметрии, то окружность является вырожденным случаем эллипса.
Если же этим следствием в рамках текущей задачи можно пренебречь, то тогда окружность можно считать частным случаем эллипса.
с математической точкитреугольник - не многоугольник. ибо 3 - не так уж и много

с математической точки зрения квадрат - не прямоугольник.в целом, да.
если же формально подходить, то в зависимости от того, какой набор свойств берется для рассмотрения.
ps
каверзные вопросы:
1. является ли точка квадратом? (это квадрат нулевого размера)
2. является ли вся плоскость квадратом? (это квадрат бесконечного размера)
3. может ли фигура одновременно быть и кругом, и квадратом?
треугольник - не многоугольник. ибо 3 - не так уж и многовот это уже редко.
потому что нет интересных (которые обладают весомыми следствиями) свойств, которые пропадают при переходе от многоугольника (с числом углов больше 3) к треугольнику.
вот двухугольник многоугольником не является, потому что сразу дохнут почти все свойства
ps
или более строго:
треугольник является частным случаем многоугольника
двухугольник является вырожденным случаем многоугольника
треугольник - не многоугольник. ибо 3 - не так уж и многодля носителей языков из индоевроейской семьи (а язык кодирует образ мыслей) три - это много, ибо у нас исторически три степени множественности: один-два-много
> для носителей языков из индоевроейской семьи
А вдруг он какой-нибудь узбек или вообще негр?
---
"Верь сводке погоды, но доверяй --- интуиции.
Будь особенно бдителен, когда всё хорошо и нет поводов для тревоги."
А вдруг он какой-нибудь узбек или вообще негр?
---
"Верь сводке погоды, но доверяй --- интуиции.
Будь особенно бдителен, когда всё хорошо и нет поводов для тревоги."
все может быть. Но исторически понятия многоугольников развивали индоевропейцы
можно ввести промежуточную меру симметрии между 2 и бесконечностью, тогда скачка не будет 

я не умею такое. Покажи как 

Нет, как ни крути, у эллипсов две оси ведь.
Если для термина эллипс фиксируется, что эллипс обладает свойством (следствием что он имеет две оси симметрии, то окружность является вырожденным случаем эллипса.У тебя древовидные структуры наследования объектов в С#-по образных языках, похоже, вызвали необратимые органические изменения в мозге. В жизни объекты обладают многими свойствами и их можно организовывать в деревья наследований многими способами, но только один способ является каноничным в конкретном контексте. В контексте школьной математики абсолютно 100% окружность является частным случаем эллипса, даже нет смысла объяснять почему. Ты же, руководствуясь нелепым желанием докопаться на ровном месте до очевидных вещей, приводишь бредовые аргументы. С тем же успехом можно утверждать, что эллипс и окружность разные вещи, потому что одним играют в рэгби, а вторым в футбол. Такие как ты - враги науки, потому что вы отвлекаете других людей от реальных дел схоластическими спорами относительно терминологии.
Если же этим следствием в рамках текущей задачи можно пренебречь, то тогда окружность можно считать частным случаем эллипса.
Никого они не отвлекают, только себя развлекают и ЧСВ тешут.
только один способ является каноничным в конкретном контекстеесли канонический, в смысле исторически сложилось, то да - окружность частный случай эллипса.
если же канонический, в смысле самое корректное определение, то окружность - это вырожденный случай эллипса
В контексте школьной математики абсолютно 100%
Такие как ты - враги науки, потому что вы отвлекаете других людей от реальных дел схоластическими спорами относительно терминологии.
Наука получается тогда, когда ставятся под сомнение зазубренные в школе истины.
посомневайся что 2+2=4, очень продуктивно
PS в 10-чной системе счисления, а то опять демагогию разведёшь
PS в 10-чной системе счисления, а то опять демагогию разведёшь

посомневайся что 2+2=4, очень продуктивноэто было бы смешно, если бы не было так грустно.
я в пяти группах (а это поболее 100 человек где геодезию веду, расписывал три варианта якобы этого решения - буквально 2-3 человека нашли ошибки, остальные смотрят и вся аргументация вида "этого не может быть, потому что не может быть, нас еще в школе учили, то 2+2=4"
Наука получается тогда, когда ставятся под сомнение зазубренные в школе истины.Есть разница между сомнением в истинах и незначительными изменениями сложившейся терминологии.
Иногда нужно рассматривать отдельно окружности и отдельно эллипсы с ненулевым эксцентриситетом, иногда не нужно. В чем тут сомнение в истинах?
тебя древовидные структуры наследования объектов в С#-по образных языках, похоже, вызвали необратимые органические изменения в мозге.Вот поэтому я говорю, что в школе надо изучать CLOS, а не C#.
У эллипса есть ровно две оси симметрии, а у круга - бесконечное количество. По этому признаку они и различаются. Ибо нет гладкого перехода от 2 к бесконечности.Это, как ни парадоксально, есть очень глубокая вещь, причем имеющая прямое отношение к оптике (да, и, скорее всего, к физике любых волн даже экспериментально много чего можно померить. Речь идет о разрывах фазы или угла поворота поляризации излучения (пафосно называют их сингулярностями) при непрерывном распределении поля. Расскажу о втором, ибо нагляднее и мне ближе — одна из побочных тем моих исследований. Итак, пусть по пучку излучения имеется неоднородное распределение угла поворота поляризации Ф(x, y) и степени ее эллиптичности, причем в некоторых точках поляризация является круговой — т.е. угол поворота в них не определен. В таких точках возможен скачок угла поворота на 180 градусов. И что, скажете вы: 0 и 180 градусов — одно и то же. И казалось бы, прибавляя или вычитая нужное число раз по 180 градусов, можно сделать зависимость Ф(x, y) гладкой. А вот нельзя... Любую зависимость Ф(x, y = const) можно, а Ф(x, y) — не получается. Эти сингулярности поляризации даже имеют якобы какой-то практический интерес, как маркер сигнала искусственного происхождения, ибо закон сохранения топологического заряда запрещает ей так просто скончаться... Да, это имеет прямое отношение к топологии, в которой я мало что понимаю. Да, что там. Ничего не понимаю. Кстати, господа-мехматяне, порекомендуйте какой-нибудь очень-очень простой учебник по топологии. Типа "Топология для умственно отсталых"...
Кстати, господа-мехматяне, порекомендуйте какой-нибудь очень-очень простой учебник по топологии. Типа "Топология для умственно отсталых"...Дубровин, Новиков, Фоменко Современная геометрия - избирательно читать.
Прасолов Элементы комбинаторной и дифференциальной топологии и Элементы теории гомологий.
Спасибо, позырить надо будет на досуге. Но слова страшные:
Элементы комбинаторной и дифференциальной топологии и Элементы теории гомологий.А что из вышеизложенного популярнее? Второе, со страшными словами?
Это, как ни парадоксально, есть очень глубокая вещь, причем имеющая прямое отношение к оптикеЭто вообще имеет отношение к физике весьма фундаментальное. Ведь в математике нет подводных камней. Если что-то получилось, то получилось раз и навсегда, ибо истина. А в физике нет истины, а есть приближенные модели. И то что получилось в одной модели, при более детальном рассмотрении может совсем даже измениться в другую сторону.
Математики отказываются это принимать в этом треде. Типа если реальность отличается от их идеальных конструкций, то тем хуже для реальности.
А что из вышеизложенного популярнее? Второе, со страшными словами?Вторая книжка это как бы вторая часть первой.
Это вообще имеет отношение к физике весьма фундаментальное... в физике нет истины, а есть приближенные модели. И то что получилось в одной модели, при более детальном рассмотрении может совсем даже измениться в другую сторону.Это да. Типа сегодня это малая поправка, а завтра именно этот эффект мы и исследуем. С этой точки зрения, мне сдается, эллипс — сегодня круг, а завтра — не круг, как захотим... Или аморфное тело — когда надо твердое, когда надо жидкое...
Математики отказываются это принимать в этом треде. Типа если реальность отличается от их идеальных конструкций, то тем хуже для реальности.
По этому треду судить сложно, слишком уж он флудовый, но в целом да...
И да, я отвечал за ту область физики, за которую отвечаю. Т.е. за оптику.
Вторая книжка это как бы вторая часть первой.Ой, мама...
Собственно не обязательно обе части читать.
Математики отказываются это принимать в этом треде. Типа если реальность отличается от их идеальных конструкций, то тем хуже для реальности.Ты как-то странно видишь природу этого спора.
Я не сомневаюсь, но все равно ссыкотно начинать... Можно от этого безобразия испытать удовольствие?..
Лучше пожалуй Дубровина Новикова Фоменко почитать он мне кажется ближе к физике.
Спасибо... А какая-нибудь просто популярная книжка для детей есть?
Ну не знаю может быть Фоменко Наглядная геометрия и топология, формул и теорем мало, картинок много, так по уровню студенту первого курса по силам. (В конце много упоротой живописи Фоменко.)
Ты как-то странно видишь природу этого спора.я должен уточнить: имелись в виду не математики как ученые, а конкретно математический авторитаризм развитый отдельными людьми в этом треде.
Во! Это мой вариант для начала. А то с точки зрения нелинейной оптики у меня все в ажуре, но пока результаты могу получать только численно — никаких аналитических оценок... Ну, для топологических свойств. За исключением самых примитивных... Коллеги, конечно, умеют, но и я хочу.
я должен уточнить: имелись в виду не математики как ученые, а конкретно математический авторитаризм развитый отдельными людьми в этом треде.Ну так самый умный здесь это ты!
Есть каноническое определение и дано оно не спроста, но это не означает, что разница между окружностью и общим эллипсом не является существенной в каких-то случаях.
Кстати, ха-ха, специально про даркгрея http://en.wikipedia.org/wiki/Circle-ellipse_problem
Кстати, ха-ха, специально про даркгрея http://en.wikipedia.org/wiki/Circle-ellipse_problemВо, это прикольно.
Ну так самый умный здесь это ты!
Нет, мне просто хочется оживить раздел. Например, твоя ссылка, как и пост Флудераста весьма познавательны, так что все было не зря.
Оживить раздел своим занудством? 

вот такие у него развлечения
а и даркгрей - один человек?
а и даркгрей - один человек?

нет это два разных
ну тут уже окружность не эллипс, так что может и вы так же
наоборот, это по вашей логике все форумчане частные случаи друг друга.
Кстати, ха-ха, специально про даркгрея http://en.wikipedia.org/wiki/Circle-ellipse_problemссылка о другой проблеме (которая в основном присуща mutable-языкам).
когда делаешь более частный класс, то появляется проблема, что есть операции (которые были у общего случая) результат которых остается частным класс, а есть которые возвращают объект обратно в общий класс.
Или другими словами:
есть общий класс A,
есть операции вида A->A,
есть свойство B', которое формирует подкласс B из класса A,
и для подкласса B часть операций A -> A являются удобными: они подкласс B преобразуют в B (B -> B а часть операций остается неудобными (B -> A
что приводит к тому, что часть задач сформулированных для частного случая B приходится всё равно рассматривать для общего случая A.
Исходный дискусс было о другом: Вырожденность vs частный случай.
Общий класс A можно рассматривать включая предельные случаи, но тогда ослабевает ряд свойств (например, у эллипса свойство осей симметрии а можно рассматривать исключая предельные случаи - тогда все свойства остаются сильными, но появляется ряд операций, который выводят объект из класса.
ps
вообще, все эти тонкости я обсуждаю не просто так. Все эти тонкости нужны для формальных выводах, в частности при автоматической проверке доказательств, или при автоматическом преобразовании знаний.
Вообще, формализованное представление дискусса выглядит следующим образом:
Есть классы A', A, B, где:
A' = A + B.
и
A' - это общий класс, который включает в себя все предельные случаи
A - это класс без предельных случаев
B - это предельные случаи
тогда:
B по отношению к A является вырожденным случаем
B по отношению к A' является частным случаем.
Сооответственно, оба утверждения верные, в зависимости от того, что называть эллипсом: класс A или класс A'
Есть классы A', A, B, где:
A' = A + B.
и
A' - это общий класс, который включает в себя все предельные случаи
A - это класс без предельных случаев
B - это предельные случаи
тогда:
B по отношению к A является вырожденным случаем
B по отношению к A' является частным случаем.
Сооответственно, оба утверждения верные, в зависимости от того, что называть эллипсом: класс A или класс A'
треугольник - не многоугольник. ибо 3 - не так уж и многодавайте введем новое семейство - малоугольники

где геодезию веду, расписывал три варианта якобы этого решения - буквально 2-3 человека нашли ошибкикакого этого? написал бы сюда подробнее, всё равно тут тред
> Математики отказываются это принимать в этом треде. Типа если реальность отличается от их идеальных конструкций, то тем хуже для реальности.зато православно
Ты как-то странно видишь природу этого спора.
один из вариантов
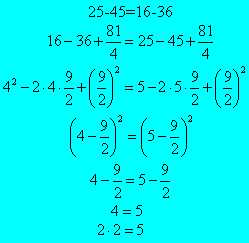
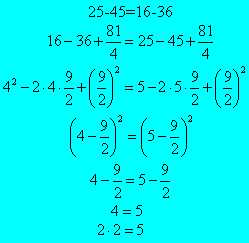
а, в этом смысле
Ещё маза не корень из a^2 извлекать с разными знаками, а на 0 сократить
Тормозят, ну ты садист, дробей наворочал. Ты их таблицу умножения поспрашивай.
А если знают, предложи им прикол для младших школьников, пусть хором быстро отвечают, 5ю 5, 6ю 6, 7ю 7. Наверно 25, 36 и 47.
Ещё маза не корень из a^2 извлекать с разными знаками, а на 0 сократить
Тормозят, ну ты садист, дробей наворочал. Ты их таблицу умножения поспрашивай.
А если знают, предложи им прикол для младших школьников, пусть хором быстро отвечают, 5ю 5, 6ю 6, 7ю 7. Наверно 25, 36 и 47.
5ю 5, 6ю 6кстати да, нетривиально что это следует из наличия нулевого и единичного элементов и десятичной системы счисления. Как задачу можно например спросить: какие числа обладают таким же свойством в 11- и 12-ричных системах счисления

Sergey79
Кстати, я тут подразобрался в вопросе. И с математической точки зрения круг - не эллипс. У эллипса есть ровно две оси симметрии, а у круга - бесконечное количество. По этому признаку они и различаются. Ибо нет гладкого перехода от 2 к бесконечности.Вот в аффинной геометрии эллипс и круг - одно и то же, ибо можно сделать гладкое преобразование одного в другое. А в евклидовой геометрии такого не допускается.