Математика в школе
Строго говоря, если соблюдая все размерности перемножать чашки и куски сахара, ответ должен быть в чашко-кусках сахара. 
Книжка написана для тебя, юный падаван.
Куски, чашки и все прочие штуки безразмерны.
Куски, чашки и все прочие штуки безразмерны.
забавно, что буквально на днях имел спор с матерью, учителем математики.
Мать уверяла меня, что ПРАВИЛЬНОЕ решение - это 2*9.
Также, с её слов, все учителя старой школ придерживаются этого
что значит безразмерны? Размерности есть
Мать уверяла меня, что ПРАВИЛЬНОЕ решение - это 2*9.
Также, с её слов, все учителя старой школ придерживаются этого
Куски, чашки и все прочие штуки безразмерны.
что значит безразмерны? Размерности есть
Чо за бред? Никогда про такое не слышал. Сам работал учителем математики, ни в одной методички такой хуйни не было. В детстве ни разу из учителей никто такой ахинеи не нес, а я никогда не задумывался как расставлять множители, как удобно так и расставляешь.
Обычно большее число первым-так удобнее в уме считать, но это не обязательно.
Обычно большее число первым-так удобнее в уме считать, но это не обязательно.
Я помню, когда я в начальной школе учился, у нас тоже какая-то такая фигня была. Но я так тогда и не понял её смысла. Хорошо хоть, обязательным выполнение этих правил не было.
а я никогда не задумывался как расставлять множители, как удобно так и расставляешь.вот примерно такая и моя аргументация была, типа "от перестановки множителей ответ не меняется".
На это старые учителя (в лице матери приводят аргумент
2+2+2+2+2+2+2+2+2=18 (2 литра молока от 9 коров)
2*(1+1+1+1+1+1+1+1+1)=18
2*9=18
По мне - ковыряние в этой мелочи что-то сродни возне, с какой стороны яйцо разбивать, с тупой или с острой, но как оказывается, есть люди, для которых это принципиально
Строго говоря, если соблюдая все размерности перемножать чашки и куски сахара, ответ должен быть в чашко-кусках сахара.5 чашек * 2 куска/чашка = 10 кусков.
Давно боюсь отдавать своих в школу... и понимаю, что с каждым годом всё сложнее будет найти учителей старой закалки, которые вдалбливали в нас знания.
Остаётся лишь выискивать на даче свои старые учебники и учить детей самостоятельно.
2 сахара × 5 раз = 10 сахара
Остаётся лишь выискивать на даче свои старые учебники и учить детей самостоятельно.
2 сахара × 5 раз = 10 сахара
2 сахара × 5 раз = 10 сахара10 сахара х раз же!
Строго говоря, если соблюдая все размерности перемножать чашки и куски сахара, ответ должен быть в чашко-кусках сахара.Отлично написано-размерности в формуле можно рассматривать как множители и тоже переставлть как хочешь, сокращать и т.д.
5 чашек * 2 куска/чашка = 10 кусков.
Просто в данной задаче размерности не такие тривиальные
Отлично написано-размерности в формуле можно рассматривать как множители и тоже переставлть как хочешь, сокращать и т.д.нет, например 2 литра * 5 г/литр - не то же самое что 2 г * 5 литров/литр
А вот еще задача:
Дано: 3 чиновника из министерства образования поделили поровну и съели 9 морковок.
Вопрос: сколько овощей съел каждый из чиновников?
Дано: 3 чиновника из министерства образования поделили поровну и съели 9 морковок.
Вопрос: сколько овощей съел каждый из чиновников?
* (коэффициент чиновника)
Не, просто безразмерное 3.
Это же чиновники, они и по 6 могут съесть.
нет, например 2 литра * 5 г/литр - не то же самое что 2 г * 5 литров/литрВ чем отличия?
Или ты имеешь в виду литров/литр типа углекислого газа в воде? Тогда эти литры нельзя сокращать потому что это разнаые размерности хоть и называются одним словом
Путин обыграл меня, сцуко, на моем поле.В школе учат ахинее всей подряд?
Это Путин виноват!
2 литра * 5 г/литр - не то же самое что 2 г * 5 литров/литра 5 г/литр * 2 литра - то же самое?
Давайте дружно найдем эту Белошистую, вскрошим ей табло, а затем сожжем ее на костре из ее собственных книг.
По поводу ваших здесь бурных обсуждений. От перестановки мест слагаемых значение суммы не изменяется, от перестановки мест множителей значение произведения не меняется - когда я учился в начальных классах, помню, это были самые важные законы, которые нам пытались вдолбить. А вот Белошистой это, видимо, никто не вдолбил. Я серьезно считаю, что это преступление - забивать детям мозг ненужной херней, которая отвлекает их от познания абстрактной сути математики. 2*5 или 5*2 - это всего лишь численный расчет, и "2" и "5" в самом расчете уже просто абстрактные числа, а не корзины и куски. Корзины и куски были в пояснении, почему для получения ответа нужно перемножать именно ЭТИ числа, а не другие.
По поводу ваших здесь бурных обсуждений. От перестановки мест слагаемых значение суммы не изменяется, от перестановки мест множителей значение произведения не меняется - когда я учился в начальных классах, помню, это были самые важные законы, которые нам пытались вдолбить. А вот Белошистой это, видимо, никто не вдолбил. Я серьезно считаю, что это преступление - забивать детям мозг ненужной херней, которая отвлекает их от познания абстрактной сути математики. 2*5 или 5*2 - это всего лишь численный расчет, и "2" и "5" в самом расчете уже просто абстрактные числа, а не корзины и куски. Корзины и куски были в пояснении, почему для получения ответа нужно перемножать именно ЭТИ числа, а не другие.
Или ты имеешь в виду литров/литр типа углекислого газа в воде?А вот почему это ты меня спрашиваешь?
Ты сказал, что можно как угодно переставлять, я переставил - объясняй теперь, что получилось.
5 чашек * 2 куска/чашка = 10 кусков.2 куска/чашка * 5 чашек = 10 кусков
школа - это по большей части способ занять детей, пока взрослые на работе
и учат там не столько профильным знаниям, сколько как жить в обществе по правилам; правила бывают глупыми или могут казаться глупыми, ребёнка учат, что всё равно может быть атата, если нарушить - а может и не быть; соответственно на выходе получается годный рашкован (или гейропеец, или пиндос - смотря по чьим обычам обучали)
то есть, деньги считать он всё равно научится, хоть в каком порядке записывай умножение
коммутативные кольца в первом классе он всё равно не поймёт
если серьёзно будет заниматься математикой, то всё равно надо будет переучиваться - ну нет столько хороших преподавателей математики, чтоб хватило на каждую школу, и для общества было бы невыгодно их так использовать, даже если бы были
и учат там не столько профильным знаниям, сколько как жить в обществе по правилам; правила бывают глупыми или могут казаться глупыми, ребёнка учат, что всё равно может быть атата, если нарушить - а может и не быть; соответственно на выходе получается годный рашкован (или гейропеец, или пиндос - смотря по чьим обычам обучали)
то есть, деньги считать он всё равно научится, хоть в каком порядке записывай умножение
коммутативные кольца в первом классе он всё равно не поймёт
если серьёзно будет заниматься математикой, то всё равно надо будет переучиваться - ну нет столько хороших преподавателей математики, чтоб хватило на каждую школу, и для общества было бы невыгодно их так использовать, даже если бы были
хорошо сказал
5 чашек * 2 куска/чашка = 10 кусков.Да именно это я и написал в Study в юморе, они не понимают размерности, поэтому учат уже лет двадцать детей этой чуши что надо ставить на первое место тот множитель, в котором размерность совпадает с ответом.
Они просто не понимают, что у второго множителя в размерности дробь и нежелательная им размерность сократится.
Своим я говорил - "Ззабей, этого маразма в старшей школе не будет. Если учитель придирается - ставь на первое место тот множитель, который он требует."
У них в начальной школе ещё и некоммутативность сложения, в задачах типа "на ветке сидело 3 птицы, потом к ним ещё 2 прилетели и сели на ветку" тоже требуют на первое место ставить слагаемое кто сидел на ветке.
А то они наверно думают, что если на первое место поставить тех кто прилетел, то у них получится что 5 птиц летает, а не на ветке сидит.
Маразматики.
Тогда эти литры нельзя сокращать потому что это разнаые размерности хоть и называются одним словомСокращают же! Отсюда и удельное сопротивление в Ом*см, хотя по правилам оно в Ом*см^2/см, и всякие вещи типа 1% раствор, хотя это означает, что содержание вещества 10 г/кг.
Интересная мысль, но если перейти на предлагаемый тобой уровень абстракции, то и тут фейл: если они не умеют математику, то, вполне вероятно, они и не умеют, как жить в обществе по правилам. То есть из-за ебанутой методички (возможно, другой) вырастят самоубийцу, убийцу, ну или просто гандона.
то и тут фейл: если они не умеют математику, то, вполне вероятно, они и не умеют, как жить в обществе по правилам.не очевидно
ясно же, что цели сделать из каждого ученика математика нет
но некоторые всё равно смогут стать математиками
но цель сделать из каждого рашкована есть - это одна из задач школы
почему считаешь, что с этим плохо справляются?
но цель сделать из каждого рашкована есть - это одна из задач школыОтлично справляются. А с введением православия в школе справляться будут еще лучше!
почему считаешь, что с этим плохо справляются?
Потому что вокруг многовато гандонов, очевидно. Примерно столько же, сколько и не-математиков.
И, кстати, неверно, что цель "сделать рашкована" одобряется мной, о чем, собственно, в первом посте было написано.
И, кстати, неверно, что цель "сделать рашкована" одобряется мной, о чем, собственно, в первом посте было написано.
У них в начальной школе ещё и некоммутативность сложения, в задачах типа "на ветке сидело 3 птицы, потом к ним ещё 2 прилетели и сели на ветку" тоже требуют на первое место ставить слагаемое кто сидел на ветке.Кстати, расскажите, как доказывается коммутативность умножения. Ну, то есть, если строго вводить операцию умножения как a*b = a + a + ... + a (b раз то совсем не очевидно, что a + a + ... + a (b раз) = b + b + ... + b (a раз).
Потому что вокруг многовато гандонов, очевидно.Очевидно, что если приравнять рашкована к гандону, то все ок.
Кстати, расскажите, как доказывается коммутативность умножения.Сделай прямоугольник из a*b кусочков сахара и посчитай, сколько сахара всего - сколько во всех рядах, сколько во всех столбцах. Только аккуратнее с чашками!
Потому что вокруг многовато гандонов, очевидно.в сравнении с чем?
тут надо сравнивать не с идеальными эльфами в лориене, а с тем, что было бы при других методах обучения (учитывая и затраты на эти методы, и возможные другие недостатки)
но в данном случае даже не сравнивает никто, это традиционный способ (тут уже написали, что некоторые учителя старой школы одобряют, в то время как твоего сына учат умножению не так - то есть походу это как раньше было отдано на усмотрение учителя по факту, так и сейчамс) - то есть скорее всего он приводит к поддержанию привычной концентрации гандонов;
а вот если предлагать новые методы, то уже их надо обосновывать как следует - потому что за старым авторитет традиции
И, кстати, неверно, что цель "сделать рашкована" одобряется мной, о чем, собственно, в первом посте было написано.тогда тебе конечно лучше побольше учить самому, и в идеале в школу не отдавать; и неважно, путин или кот
Давайте дружно найдем эту Белошистую, вскрошим ей табло, а затем сожжем ее на костре из ее собственных книг.надо бы
там в школе такого дерьма по самое горло.
Пришлось тут как-то с семиклассницей физикой-математикой заниматься - просто ужас. Что размерности в задаче сходятся отдельном столбике анализируют, бездумно переводят в Си даже если там надо посчитать на сколько за 2 часа вырос цветок, если скорость роста по 2 мм/час, оформление - шаг вправо-влево - побег и расстрел, снижают отметки. По математике не так как было, а так как удобнее анализировать нарисуешь прямоугольники в иллюстрации к задаче - карают. И т.д.
Бедные дети. Немудрено, что у них появляется стойкое отвращение к так преподаваемым предметам.
Куда деваться от этих идиотов?
Да мне как-то насрать на концентрацию гандонов в общесте (я и сам еще тот гандон, конечно). Какая методика вырастит сколько гандонов - вопрос к докторам пед. наук, понятно, что он выходит за рамки первого поста.
Но дык мне не насрать на то, как воспитывают моих детей.
Я понимаю твою тягу к абстрагированию, у тебя детей нет, плюс ты математик. Но я уже не математик, наверное, и проблема для меня вполне конкретна. Не до абстракций.
Но дык мне не насрать на то, как воспитывают моих детей.
Я понимаю твою тягу к абстрагированию, у тебя детей нет, плюс ты математик. Но я уже не математик, наверное, и проблема для меня вполне конкретна. Не до абстракций.
тогда тебе конечно лучше побольше учить самому, и в идеале в школу не отдавать; и неважно, путин или котВажно: именно из тех же соображений качества конечного продукта меня некогда отдали в школу.
Важно: именно из тех же соображений качества конечного продукта меня некогда отдали в школу.откуда же взялись все гандоны, если они учились в таких же школах?
где-то у тебя что-то не сходится
и проблема для меня вполне конкретна. Не до абстракций.у тебя в первом посте абстракция - путин
потому что конкретный Путин вовсе ничего не имеет против твоего конкретного сына, это система такая (абстрактное понятие)
Разрешите и мне вставить пару комментариев?
Во-первых, так получилось, что в Советском Союзе на определенном этапе педагогов-математиков начали набирать из педагогов, а не из математиков. Я искренне убежден, что день, когда это случилось, нужно объявить национальным трауром и отмечать каждый год минутой молчания, но даже это недостаточно, чтобы понять всю глубину трагедии.
На самом деле, всё логично. Строгое следование форме позволяет подготовить человека к решению сложных задач - в сложных задачах часто возникают (глупые) ошибки, и в строгой записи их намного легче найти. Но педагогам это очевидно, и они НЕ объясняют это детям и молодым педагогам. Хотя сам факт существования правила "надо оформлять, потому что так надо" должен насторожить любого человека разумного.
Во-вторых, учеником пропущен этап построения математической модели. Я понимаю, что словосочетание "математическая модель" звучит страшнее иного рассказа Хичкока, но без неё невозможно формализовать ошибку в примере. Что характерно, начиная с 1958 года в Советском Союзе была внедрена экспериментальная методика обучения школьников. В ней ученики должны последовательно совершать следующие действия: формулировать условие -> самостоятельно искать решение для общего случая -> использовать найденное решение для сформулированного условия. В такой постановке, очевидно, нет места для ошибки "неправильно записал множители".
В-третьих, многие форумчане правильно заострили внимание на том, что в школе не даётся понятие размерности и безразмерных величин. Во всяком случае, не даётся до пятого класса, когда начинается физика.
Во-первых, так получилось, что в Советском Союзе на определенном этапе педагогов-математиков начали набирать из педагогов, а не из математиков. Я искренне убежден, что день, когда это случилось, нужно объявить национальным трауром и отмечать каждый год минутой молчания, но даже это недостаточно, чтобы понять всю глубину трагедии.
На самом деле, всё логично. Строгое следование форме позволяет подготовить человека к решению сложных задач - в сложных задачах часто возникают (глупые) ошибки, и в строгой записи их намного легче найти. Но педагогам это очевидно, и они НЕ объясняют это детям и молодым педагогам. Хотя сам факт существования правила "надо оформлять, потому что так надо" должен насторожить любого человека разумного.
Во-вторых, учеником пропущен этап построения математической модели. Я понимаю, что словосочетание "математическая модель" звучит страшнее иного рассказа Хичкока, но без неё невозможно формализовать ошибку в примере. Что характерно, начиная с 1958 года в Советском Союзе была внедрена экспериментальная методика обучения школьников. В ней ученики должны последовательно совершать следующие действия: формулировать условие -> самостоятельно искать решение для общего случая -> использовать найденное решение для сформулированного условия. В такой постановке, очевидно, нет места для ошибки "неправильно записал множители".
В-третьих, многие форумчане правильно заострили внимание на том, что в школе не даётся понятие размерности и безразмерных величин. Во всяком случае, не даётся до пятого класса, когда начинается физика.
Во-первых, так получилось, что в Советском Союзе на определенном этапе педагогов-математиков начали набирать из педагогов, а не из математиков.у нас в школе как-то несколько занятий по математике провёл препод из местного вуза; никто не понял нихера, чему подтверждение - что на каждом уроке была в конце короткая контрольная, за которую все получали 2 или 3- - то есть дети не понимали ничего
поэтому я бы не сказал, что дескать нужно брать математиков, а не педагогов, и всё будет ок
Система эволюционирует под воздействием (Путина через Фурсенку). И если раньше я думал, мол, ну да, эволюционирует - плохо, да, но меня не касается, я ж и сам преподаю в крутой школе, и дети мои устроены, как надо - то вдруг выходит, что все не так, что меня уже наебали с образованием детей.
Система эволюционирует под воздействием (Путина через Фурсенку).но твой конкретный пример не подтверждает эту абстрактную теорию, так как, повторяю, уже написали в каментах, что многие учителя старой школы одобряют данный подход
Кстати, расскажите, как доказывается коммутативность умножения.Для натуральных чисел прямоугольник рисуют со сторонами a и b. И считают клеточки по строкам, потом по столбцам.
b клеток/столбец * a столбцов = a клеток/строка * b строк
Далее при переходе к целым, рациональным, действительным, комплексным числам проверяют, что всё остаётся в силе.
В коммутативных группах-кольцах-полях это просто аксиома. Зависит от природы объекта. Повороты относительно одной оси коммутируют, а относительно точки - нет.
Если тебе скомандовать сначала налево, а потом кругом, то это то же самое что кругом, а потом налево.
А если тебе скомандовать налево а потом лечь, это не то же самое что лечь, а потом налево.
Повороты в кубике Рубика некоммутативны.
Путину объективно выгодна дебилизация - легче держаться у власти, влом сейчас искать ссылку на научное исследование об устойчивости авторитарных режимов и проценте образованной-умной молодёжи.
Именно об этом тебе говорят, а не о том, что этого маразма до Путина вообще не было.
Он назначает таких министров, которые поощряют такой маразм, а не борются с ним. Грубо говоря.
Именно об этом тебе говорят, а не о том, что этого маразма до Путина вообще не было.
Он назначает таких министров, которые поощряют такой маразм, а не борются с ним. Грубо говоря.
Если тебе скомандовать сначала налево, а потом кругом, то это то же самое что кругом, а потом налево.как ты будешь объяснять ребёнку, причём здесь умножение?
А если тебе скомандовать налево а потом лечь, это не то же самое что лечь, а потом налево.
Повороты в кубике Рубика некоммутативны.
я бы не смог наверное
в россии всегда был авторитарный режим
я про то и говорю, если не хочется, чтоб сын был рашкованом - лучше не отдавать в рашкованскую школу, хоть при путине, хоть при брежневе (но я не утверждаю, что альтернативы однозначно лучше или хуже)
я про то и говорю, если не хочется, чтоб сын был рашкованом - лучше не отдавать в рашкованскую школу, хоть при путине, хоть при брежневе (но я не утверждаю, что альтернативы однозначно лучше или хуже)
Был тут в стади такой хохмопост с фоточкой тетрадки, где в тривиальной задачке (9 покупателям продали по два литра молока; спрашивается, сколько молока продано) решение "9*2=18" зачеркнуто и исправлено на "2*9=18".Это п-ц абсолютный.
Меня это дело заинтересовало, я решил проверить - правда ли этой хуйне учат моих детей. Рассмотрел учебники старшего - по счастью, все ок. Подумал, может, фейк, зашел в школьную библиотеку, спросил книжку А.В.Белошистой "Обучение решению задач в начальной школе, книга для учителя". Почитал, охуел.
То есть, то, что подобное встречается на практике, я знал. Это и сейчас так, и при Димоне, и при Борисе, и в Совке так было (да, именно оттуда, от тех самых "советских учителей", с уходом которых по мнению многих всё окончательно разрушится, всё и шло). И учителя такие, и методисты, которые учителей контролируют. То есть, даже если учитель и нормальный, ему придётся сражаться со всякими методистами, которые будут говорить ему/ей, что детей так учить нельзя. Но не подумал бы, что это в "твёрдом виде" прописано.
Самое интересное, я когда-то наблюдал, что подобные концепции защищала, например, мамашка, с очень серьёзным математическим образованием, и довольно хорошим аналитическим мышлением. Не в такой дикой форме, конечно.
Никогда не забуду, что из себя представляла физика в школе (кроме старших классов, когда физ-мат школа была). С математиками мне как-то всегда везло.
как ты будешь объяснять ребёнку, причём здесь умножение?Как хочу бинарную операцию, так и называю. Хоть композицией, хоть a звёздочка b, хоть a кружочек b, хоть сначала поворот b, потом поворот a.
я бы не смог наверное
Умножением/сложением стоит назвать если какие-то свойства операций такие же, как свойства для умножения/сложения чисел.
Мы же оставляем название числа для рациональных дробей, хотя изначально они как натуральные возникают и даже 0 не сразу исторически появился, отрицательные тоже не сразу добавились.
Обычно старое имя даём новому объекту, если у него сохраняется большая часть свойств старого объекта.
Обычно старое имя даём новому объекту, если у него сохраняется большая часть свойств старого объекта.ну у всех этих движений плоскости нет ни хера из свойств умножения натуральных чисел
кроме разве что ассоциативности (я не уверен, что смогу объяснить ребёнку про ассоциативность, я например в таком возрасте не понимал этого, а был самым умным в регионе)
а был самым умным в регионеА что за регион-то? Чечня или Дагестан?
калужская область
ну у всех этих движений плоскости нет ни хера из свойств умножения натуральных чисел кроме разве что ассоциативностиКса неточен, скажем так.
То, что он описывает с движениями, называется композицией, а не умножением.
умножение в обычном понимании: f(x)*g(x)
композиция: g( f(x) ) (как раз про движения)
и вот это как раз пример, когда термины лучше раньше времени не перегружать, иначе только каша будет.
Самое интересное, я когда-то наблюдал, что подобные концепции защищала, например, мамашка, с очень серьёзным математическим образованием, и довольно хорошим аналитическим мышлениемА и правда что плохого? Детей сразу готовят к теории групп, на которой стоит вся современная наука.
математики любят записывать композицию так же, как умножение
понять это невозможно, нужно запомнить (а если не собираешься читать статьи математиков, то можно не запоминать, ничего не потеряешь)
или как объяснить лучше?
понять это невозможно, нужно запомнить (а если не собираешься читать статьи математиков, то можно не запоминать, ничего не потеряешь)
или как объяснить лучше?
есть вещи, которые лучше раньше времени не объяснять, пока мышление не готово к подобным абстракциям. А так, это просто сокращённая запись, более удобная — когда уже есть понимание, что мы работаем с абстракцией "функция" и функциональным пространством, а не с пространствами, на которых эти функции работают. Иначе записи получатся перегруженными всяким мусором, значков хватать не будет, тяжелее воспринимать.
В общем, имхо, всё логично, просто всему своё время. Это уже не школьная математика, в любом случае.
В общем, имхо, всё логично, просто всему своё время. Это уже не школьная математика, в любом случае.
Это уже не школьная математика, в любом случае.ну хз
типа движения по поверхности земли - это что-то более абстрактное, чем яблоки или деньги?
у нас в школе регулряно вели занятия преподаватели математики и физики из вуза. Проблем не заметил, наоборот только позитивные эмоции.
у нас в школе регулряно вели занятия преподаватели математики и физики из вуза. Проблем не заметил, наоборот только позитивные эмоции.ну так я и говорю, преподы есть разные, и хороших на всех не хватит
движения — реальны и конкретны. Абстрактны и не очень нужны попытки движения по земле формализовать и запихнуть в какое-то пространство с какими-то формальными свойствами.
PS: короче, я потерял нить дискуссии.
сама по себе модель с движениями довольно удобна, чтобы к каким-то абстракциям готовить, там готовить мышление к работе с функциями, как самостоятельными объектами. Модель наглядна (в отличии от тригонометрии можно визуализировать, запрограммировать... Но мы куда-то не туда валимся. Тут мало общего с "бытовым" умножением, и лучше, поэтому, разные термины для операций использовать.
PS: короче, я потерял нить дискуссии.
сама по себе модель с движениями довольно удобна, чтобы к каким-то абстракциям готовить, там готовить мышление к работе с функциями, как самостоятельными объектами. Модель наглядна (в отличии от тригонометрии можно визуализировать, запрограммировать... Но мы куда-то не туда валимся. Тут мало общего с "бытовым" умножением, и лучше, поэтому, разные термины для операций использовать.
Но мы куда-то не туда валимся. Тут мало общего с "бытовым" умножением, и лучше, поэтому, разные термины для операций использовать.опять же в быту два раза по пять яблок, и пять раз по два яблока - разные вещи
попробуй на них накладные заполнить неправильно, например - если в крупных размерах, можно и присесть
Смысл то этого в том что
ответ на задачу это
2+2+2+2+2
а не
5+5
ответ на задачу это
2+2+2+2+2
а не
5+5
ну так я и говорю, преподы есть разные, и хороших на всех не хватитУ меня в школе программирование началось в 9-м классе. Компьютер дома появился в 10-м.
Вот, в школе был молодой препод, без пед. образования, который начал толкать материал людям, не умеющим программировать совершенно, примерно так:
Есть язык Си. Там есть операторы, они бывают унарные, бинарные, тернарные. Бывают циклы, с постусловием и предусловием. Ну и дальше в том же духе.
Естественно, никто ничего не понял абсолютно, программирование стали бояться, и учили основы на стороне (мама одного из одноклассников устраивала нам ликбез и обучила основам, что меня и спасло). Просто препод идиот, которого нельзя было допускать до занятий в школе.
Ответ на эту задачу - 10.
Давайте дружно найдем эту Белошистую, и дадим ей опросник из того исследования, про мышление средневековых людей
Но ответ то не важен - важно решение.
(я, если чё, не защищаю происки методистов)
(я, если чё, не защищаю происки методистов)
Мне жалко тех детей, которые рано просекают коммутативность умножения и, понимая физический смысл задачи, искренне не понимают, почему последовательность множителей надо писать как-то определённо 
Именно такая запись решения важна для тех, кому надо повторять, Ганс, 3 раза, 3 раза, Ганс, и не менее 3-х раз, Ганс. Для других же это прямая дорога к отвращению к учёбе или же к потере уважения к учителю, если родитель будет с мозгами нормальными
Именно такая запись решения важна для тех, кому надо повторять, Ганс, 3 раза, 3 раза, Ганс, и не менее 3-х раз, Ганс. Для других же это прямая дорога к отвращению к учёбе или же к потере уважения к учителю, если родитель будет с мозгами нормальными
ну они просто раньше других поймут, что иногда некоторые вещи стоит сделать "на отъебись", даже если знаешь лучше
например, если на работе клиент думает, что знает, чего хочет, то проще это сделать (а потом переделать, когда он поймёт, что хотел другого - надо только чтоб он заплатил за оба раза )
например, если на работе клиент думает, что знает, чего хочет, то проще это сделать (а потом переделать, когда он поймёт, что хотел другого - надо только чтоб он заплатил за оба раза
)Смысл то этого в том что
ответ на задачу это
2+2+2+2+2
а не
5+5
5+5 - тоже правильный ответ! Просто решение за ним стоит нестандартное: в каждую чашку положили по два кусочка, значит первых кусочков было 5 и вторых 5, вместе 5+5.
ну они просто раньше других поймут, что иногда некоторые вещи стоит сделать "на отъебись", даже если знаешь лучшеА в особо интересных случаях школа и родители получат саркастичного интеллектуала, троллящего с разной степенью толстости всех вокруг + манипулирующего всеми окружающими, если нет родителей, чспособных стать отдушиной (а таких очень мало, на самом-то деле). Плавали-знаем. Удовольствие не просто ниже среднего, а скажем так, на любителя.
Учить надо делать не на отъебись, а на уважении права других на ошибки. Только тогда человек даст клиенту право на ошибку, а потом предложит другое решение, и не будет беситься. И очевидно, что не с навязывания ошибочной позиции правому младшешкольнику это надо воспитывать.
Смысл то этого в том чтоА почему 2+2+2+2+2 — это обязательно 2*5, а не 5*2? Какая разница, 2 кусочка 5 раз или 5 раз по 2 кусочка?
ответ на задачу это
2+2+2+2+2
а не
5+5
Учить надо делать не на отъебись, а на уважении права других на ошибки.ну вот тут допустим учитель ошибается, и это его право нужно уважать - что не так?
причём он оценивает твою работу, а не наоборот - как и во взрослой жизни будет
В случае с клиентом клиент вредит только себе, так как всё-равно заплатит и за правильное решение, и за первое неправильное. Если же платить он будет только 1 раз, то в данном случае придётся страдать за ошибку, и никакого заведомого права уважать такую ошибку я не вижу. Я предлагаю уважать право на ошибку, которые тебе непосредственно мало чем грозит. Ошибка учителя в данном случае имеет прямое отношение к ребёнку, и я не склонна учить благодушно относится к ним. Вернее даже так - такие ошибки надо иногда уметь игнорировать (а учителю надо уметь извиняться за них, так как игра в одни ворота - см. пункт про тролля-интеллектуала но нельзя на них учить младшешкольника. Так как это явно несправедливо по отношению к нему, а воспитывать на несправедливости с самого начала жизни в школе - это эпик фейл.
А почему 2+2+2+2+2 — это обязательно 2*5, а не 5*2? Какая разница, 2 кусочка 5 раз или 5 раз по 2 кусочка?В школе замечал как-то, что обычным детям очевидно, что повторяющееся слагаемое надо ставить на первое место. Почему - хз, меня это всегда удивляло.
ну у всех этих движений плоскости нет ни хера из свойств умножения натуральных чиселЗдрасьте Вам!
кроме разве что ассоциативности (я не уверен, что смогу объяснить ребёнку про ассоциативность, я например в таком возрасте не понимал этого, а был самым умным в регионе)
(a+b)+c = a+(b+c)
То же для умножения
Ассоциативность - это Сочетательный закон - слышал в школе такие слова? Если не слышал, значит или учительница плохая, или программа математики была плохая
или это дело рук Карбофоса или одно из двух (с) Следствие ведут колобки
У всех этих движений есть свойства
0. Для любых a и b определено движение c = a*b (сначала выполняем движение b, потом a)
1. a*(b*c)=a*(b*a) ассоциативность - сочетательный закон
2. Существование единицы e*a=a*e=a для всех a (e - тождественное преобразование, когда ничего не делаем)
3. Существование обратного a^{-1}*a = a*a^{-1}=e
4. a*b = b*a коммутативность - переместительный закон
В некоторых 4 не выполняется. Бинарная операция с такими свойствами называется (сюрприз!) умножением. Если вместо единицы назвать нейтральный элемент 0, и потребовать 4 (коммутативность то называется сложением. Без коммутативности обычно всегда умножением.
Вот когда там на этом множестве две операции, то одна из них обычно сложение, вторая умножение, там ещё аксиомы появляются - дистрибутивность - распределительный закон (a+b)*c=a*b+a*c и т.д.
Чего тут такого-этакого? Композиция - умножение. не совсем прав.Это для функций на прямой есть композиция значение которой при заданом x по определению f(g(x а есть поточечное умножение f(x)*g(x).
Но если мы посмотрим на калькулятор например, то там на обратных функциях подписано sin^{-1} это вовсе не 1/sin(x) в смысле поточечного умножения, а обратная функция (арксинус) в смысле композиции функций, в смысле того, что я выше в аксиомах написал.
Никакого поточечного умножения может не быть, потому что нет никакой ложки (c)
Нет никаких иксов x вообще (или их надо специально конструировать а f и g вполне себе умножаются или складываются в смысле композиции.
В школе замечал как-то, что обычным детям очевидно, что повторяющееся слагаемое надо ставить на первое место. Почему - хз, меня это всегда удивляло.:) Вот и я о том же. По хорошему, нормальный учитель должен разобраться в причине, по которой ученик ставит другой множитель (тут была опечатка)- то ли совсем плохо понимает, о чём речь, и просто ставит 2 имеющиеся цифры задачи рядом, соединяя их знаком операции, которая проходится сейчас (умножение то ли наоборот, очень хорошо понимает и поэтому уже или играет с числами, или просто не замечает порядка расстановки множителей. И очевидно, что реакция должна быть разная - последнему не нужно снижать оценку, но и не стоит в период прохождения этой темы к доске вызывать
Если же платить он будет только 1 раз, то в данном случае придётся страдать за ошибку, и никакого заведомого права уважать такую ошибку я не вижу.ну смотри
клиент приходит и хочет чего-то неправильного
ты такая хорошо знаешь математику, и начинаешь объяснять ему, потрясая дипломом мгу, что он не прав
он злится и уходит к другому поставщику
или ты делаешь как он хочет (но имея в виду, что он скорее всего передумает и надо будет переделывать - и тут не очень важно, будет ли он платить второй раз, можно это ожидание сразу включить в счёт за первый раз)
тогда клиент более доволен, и в итоге работу ты выполняешь и деньги получаешь
даже если клиент будет считать, что ты глупая и не можешь сделать с первого раза нормально, и надо всё проверять за тобой
идеальный вариант - объяснить так, чтобы клиенту показалось, что он сам передумал, тогда он будет ещё более доволен (потому что почувствует себя умным, а работа будет сделана сразу как нужно и переделывать не придётся
но это как бы уже не на уроках математики нужно учить
Так как это явно несправедливо по отношению к нему, а воспитывать на несправедливости с самого начала жизни в школе - это эпик фейл.а что тогда делать, когда он закончит школу и увидит, что на работе правила совсем другие? сложившаяся личность может уже и не оправиться от такого удара
а что тогда делать, когда он закончит школу и увидит, что на работе правила совсем другие? сложившаяся личность может уже и не оправиться от такого удараПоэтому надо детей учить на вопрос "сколько будет 2*5" отвечать "а сколько надо?"
(a+b)+c = a+(b+c)да слышал
То же для умножения
Ассоциативность - это Сочетательный закон - слышал в школе такие слова? Если не слышал, значит или учительница плохая, или программа математики была плохая
но в первом классе этого не понять, кажется
ты пробовал младшим школьникам прогонять эту всю фигню про sin^{-1} и поточечное умножение, которого нет? они не поймут
Белошистая Анна Витальевна — профессор кафедры ДиНО, д.п.н.
Образование: высшее.
Наименование ВУЗа: МГПУ.
Год выпуска: 1976.
Тема докторской диссертации: Математическое развитие ребенка в системе дошкольного и начального школьного образования.
Год защиты: 2004.
С какого года на кафедре: 1987.
Карьерный рост:
1987–1992 — ассистент;
1992–1995 — старший преподаватель;
1995–2004 — доцент;
с 2004 и по н.вр. — профессор.
Читаемые лекционные курсы:
1. Методика обучения математике в начальной школе;
2. Теория и методика развития математических представлений дошкольников;
3. Развитие математических способностей дошкольников и младших школьников;
4. Индивидуальный подход при обучении математике;
5. Внеклассная работа по математике.
Область научных интересов:
Математическое развитие детей дошкольного и школьного возраста.
Общее количество научных публикаций: 253.
Полученные Гранты:
грант НФПК в 2004 г.,
грант Рособразования в 2009 г.,
грант РГНФ в 2009.
Образование: высшее.
Наименование ВУЗа: МГПУ.
Год выпуска: 1976.
Тема докторской диссертации: Математическое развитие ребенка в системе дошкольного и начального школьного образования.
Год защиты: 2004.
С какого года на кафедре: 1987.
Карьерный рост:
1987–1992 — ассистент;
1992–1995 — старший преподаватель;
1995–2004 — доцент;
с 2004 и по н.вр. — профессор.
Читаемые лекционные курсы:
1. Методика обучения математике в начальной школе;
2. Теория и методика развития математических представлений дошкольников;
3. Развитие математических способностей дошкольников и младших школьников;
4. Индивидуальный подход при обучении математике;
5. Внеклассная работа по математике.
Область научных интересов:
Математическое развитие детей дошкольного и школьного возраста.
Общее количество научных публикаций: 253.
Полученные Гранты:
грант НФПК в 2004 г.,
грант Рособразования в 2009 г.,
грант РГНФ в 2009.
"сочетательный закон"? Не слышал. Можно ссылку на какую-нибудь книжку по теории групп, где он описан?
Вот, нет никакого "сложения" или "умножения". В абстрактных группах, которые ты сейчас определяешь (ну тут, в треде, у большинства математическое образование, всё-таки есть просто некая операция, которая обозначается жирной точкой (в противовес обычной точке звездой или кружочком. И "умножением" её просто не принято называть, причём, я сейчас посмотрел английское/французское/немецкое определения (на Вики там тоже "умножения" в определениях нет.
Ближе всего "композиция".
Про сложение-умножения вспоминают, когда начинают "кольца" толкать, в общем конструкции, где обе операции присутствуют, и в общем они описывают все привычные модели.
Можно сказать так: умножения в отрыве от сложения не существует. Хотя при желании, можно ввести операцию "+", называть её "умножением", а подразумевать под ней деление. Но никому такая каша не нужна
Вот, нет никакого "сложения" или "умножения". В абстрактных группах, которые ты сейчас определяешь (ну тут, в треде, у большинства математическое образование, всё-таки есть просто некая операция, которая обозначается жирной точкой (в противовес обычной точке звездой или кружочком. И "умножением" её просто не принято называть, причём, я сейчас посмотрел английское/французское/немецкое определения (на Вики там тоже "умножения" в определениях нет.
Ближе всего "композиция".
Про сложение-умножения вспоминают, когда начинают "кольца" толкать, в общем конструкции, где обе операции присутствуют, и в общем они описывают все привычные модели.
Можно сказать так: умножения в отрыве от сложения не существует. Хотя при желании, можно ввести операцию "+", называть её "умножением", а подразумевать под ней деление. Но никому такая каша не нужна
или ты делаешь как он хочет (но имея в виду, что он скорее всего передумает и надо будет переделывать - и тут не очень важно, будет ли он платить второй раз, можно это ожидание сразу включить в счёт за первый раз)Т.е. всё-равно будет оплачено и правильное, и неправиьное решение, т.е. ты не страдаешь. ЧТД
Ты зря думаешь, что делать на отъебись с младшей школы - это здорово. БОльшая часть школьных поганцев вырастает как раз из тех, кто на отлично усвоил выполнение на отъебись и перед которым никогда не извинялись за ошибки, допущенные по отношению к ним. Т.е. они отлично усваивают
а) примат формы перед содержанием
б) примат власти и силы перед правотой
Ты уверен, что тебе было бы комфортно рядом с такими людьми?
Т.е. всё-равно будет оплачено и правильное, и неправиьное решение, т.е. ты не страдаешь.ну в смысле не страдаешь
мне ненужную работу делать неприятно, например
БОльшая часть школьных поганцев вырастает как раз из тех, кто на отлично усвоил выполнение на отъебись и перед которым никогда не извинялись за ошибки, допущенные по отношению к ним.Почему думаешь, что никогда не извинятся? Учителя тоже разные.
В начальной школе переместительный, сочетательный и распределительный закон/свойство это в школе так официально называется, соответственно это в вузе и в науке
коммутативность, ассоциативность, дистрибутивность
google сочетательный закон сложения
Результатов: примерно 815 000
если не слышал, то странно. Или троллишь, раз рядом про группы говоришь, какие группы в начальной школе?
Это как предлагает мне про арксинус рассказать в начальной школе
как я узнаю стул, хотя я впервые его вижу? Он обладает его свойствами, тех стульев, что я пользовался до того.
Уверяю тебя, бинарная операция в группе называется умножение или сложение, обычно в зависимости от того, называем ли мы нейтральный элемент нулём или единицей. Композиция тоже называется.
От происхождения группы часто как мы операцию в ней называем зависит.
Умножение матриц. Для матриц в одну строчки и столбик превращается в умножение. Сложение матриц тоже.
А по поводу твоей шутки про взять умножение, обозначить +, а иметь в виду деление -
Не обладает эта операция свойствами умножения, а бинарная операция в группах обладает, ну сядь на стол, а комп поставь на стул и пиши ногами.
коммутативность, ассоциативность, дистрибутивность
google сочетательный закон сложения
Результатов: примерно 815 000
если не слышал, то странно. Или троллишь, раз рядом про группы говоришь, какие группы в начальной школе?
Это как предлагает мне про арксинус рассказать в начальной школе
как я узнаю стул, хотя я впервые его вижу? Он обладает его свойствами, тех стульев, что я пользовался до того.
Уверяю тебя, бинарная операция в группе называется умножение или сложение, обычно в зависимости от того, называем ли мы нейтральный элемент нулём или единицей. Композиция тоже называется.
От происхождения группы часто как мы операцию в ней называем зависит.
Умножение матриц. Для матриц в одну строчки и столбик превращается в умножение. Сложение матриц тоже.
А по поводу твоей шутки про взять умножение, обозначить +, а иметь в виду деление -
Не обладает эта операция свойствами умножения, а бинарная операция в группах обладает, ну сядь на стол, а комп поставь на стул и пиши ногами.
бинарная операция в группе называется умножение или сложение, обычно в зависимости от того, называем ли мы нейтральный элемент нулём или единицей.охеренно, как ты собрался детям рассказывать, что одно и то же можно назвать нулём, а можно единицей? они отлично знают, что одно яблоко и нет яблок - сильно разные вещи
Во всяком случае, не даётся до пятого класса, когда начинается физика.а чо, в рашке физика уже с 5го класса?
От перестановки мест слагаемых значение суммы не изменяется, от перестановки мест множителей значение произведения не меняетсяВообще в праведном гневе вы малость путаете сами математические выкладки и методические рекомендации по обучению этим математическим выкладкам.
На самом деле в описанной идее есть смысл(точнее был смысл до того как эту идею несколько раз перефразировали переписывая из методички в методичку доблестные педагогини, каждый раз подгоняя её под свое (не)понимание сути вопроса). То есть если я как учитель преподаю в начальной школе и учу детей умножению, то мне опять же как учителю методически правильнее придерживаться различных соглашений. Хотя с точки зрения математики эти соглашения никакого смысла не несут, но преподавание и понимание они во многом облегчают.
Так например, если бы я объясняла умножение как "взять столько-то раз по столько-то штук" я бы тоже, когда писала сама на доске, писала бы с однозначным порядком множителей, несмотря на возможность перестановки слагаемых.
Собственно умение вырабатывать такие соглашения и методические приемы и отличает педагога от ученого.
Важно только понимать:
1) Это рекомендация для преподавателя а не обязательные требования к ученику
То есть если преподаватель начальной школы напишет на доске множители в неправильном порядке - это его недочет как педагога, но если школьник напишет так в домашней работе - это правильной решение математической задачи.
2) Злоупотребление такими соглашениями мешает иногда видеть задачу в более общей постановке. Типа того что ребенок которого за пять лет натаскали решать уравнение a*x + b = c, уравнение a*y + b =c решить сходу не сможет.
Собственно автор методички плохой педагог не потому, что она сказала что-то математически неверное, а потому что она не понимает пункт 1)
о привет, только вчера тебя вспоминала
Смысл то этого в том чтоПять раз по два, то есть 5*2.
ответ на задачу это
2+2+2+2+2
как я рассказывал как собирать кубик Рубика или про игру пятнадцать - тождественное преобразование когда мы ничего не трогаем - тоже преобразование - играет роль единицы. Выполнение поворотов одно за другим играет роль умножения. Оно похоже на обычное, но некоммутативно (они этого слова обычно не знают, им надо говорить нарушено переместительное свойство операции, играющей роль умножения). Тебе же надо как-то записать последовательность поворотов граней, там умножение и пишется (ну и знак умножения опускается, даже точка не пишется, а уж это точно не начальная школа) типа В^2ЛВ - где В повернуть верхнюю грань на 90, Л - левую на 90 градусов
У тебя не какая-то абстрактная группа для школьников, они тяжело это воспринимают, у тебя конкретная реализация. И тебе надо, например, объяснить почему изобретатель Лойд игры 15 назначил миллион тому, кто соберёт в исходное положение с переставленными 14 и 15, но никто не выиграл. Зато продажи пошли в гору, все пытались собрать Ты рассказываешь группу перестановок и чётность перестановки на конкретном примере на мат.кружке каком-нибудь, это же школьники
У тебя не какая-то абстрактная группа для школьников, они тяжело это воспринимают, у тебя конкретная реализация. И тебе надо, например, объяснить почему изобретатель Лойд игры 15 назначил миллион тому, кто соберёт в исходное положение с переставленными 14 и 15, но никто не выиграл.
Зато продажи пошли в гору, все пытались собрать Ты рассказываешь группу перестановок и чётность перестановки на конкретном примере на мат.кружке каком-нибудь, это же школьникиОно похоже на обычное, но некоммутативно (они этого слова обычно не знают, им надо говорить переместительное свойство умножения нарушено).На сложение похоже не меньше. Почему математики любят сравнивать с умножением, а не со сложением - понять невозможно, нужно запомнить (если хочешь чтоб математики приняли за своего).
охеренно, как ты собрался детям рассказывать, что одно и то же можно назвать нулём, а можно единицей? они отлично знают, что одно яблоко и нет яблок - сильно разные вещиИ ещё, сколько будет 2 яблока + 2 яблока более-менее понятно. А вот как умножить 2 яблока на 2 яблока? И что такое "квадратное яблоко"?
Вообще, я против лишних абстракций раньше времени.
Умножение натуральных чисел... Ну мы взяли, разложили предметы в виде прямоугольника m*n, и посчитали, сколько предметов получилось. Чтобы быстрее считать, и нужны таблицы умножения, это же очевидно. Крайне наглядно, отсюда же сразу интуитивно очевидным становится, почему умножение коммутативно.
Интуитивно очень просто разложить кусочки сахара в 2*5, и потом уже считать. И тогда абсолютно без разницы, в каком порядке умножать — после того, как сахар выложен на стол, куски сахара существуют сами по себе, без чашек/порций. Поэтому, вот эти правила, про которые говорят, это бред, они направлены на то, чтобы помешать осмыслить предмет и научить абстрагироваться.
PS: , , вы что, оба (обе?) бабы? я в шоке, честное слово.
> На сложение похоже не меньше.
обычное сложение = коммутативно и обратимо
обычное умножение = коммутативно и не обязательно обратимо
обобщенное умножение, которое композиция, и некоммутативно, и не обратимо
Так кто на кого больше похож?
обычное сложение = коммутативно и обратимо
обычное умножение = коммутативно и не обязательно обратимо
обобщенное умножение, которое композиция, и некоммутативно, и не обратимо
Так кто на кого больше похож?
коммутативную операцию можешь хоть умножением называть, хоть сложением, называют сложением a+b=b+a, а когда не коммутативно a*b не равно b*a- сложением не называют, просто не принято
Это если у тебя группа и там только одна операция как в кубике Рубика и игре 15. Когда у тебя 2 операции (кольцо - гибрид двух групп на одном множестве в каком-то смысле, одна по умножению, другая по сложению то там однозначно что сложение, а что умножение.
Потому что там у тебя две бинарных операции, и два нейтральных элемента e1 для первой операции и e2 для другой
Но! По одной операции обратные для всех элементов a есть - тогда это сложение, элементы противоположными, а не обратными называют и обозначают (-a) вместо a^{-1} а по другой операции для обратимости есть исключение - у нейтрального элемента другой операции нет обратного.
То есть (-1)=-1 существует, а 0^{-1}= 1/0 не существует.
Иногда таких элементов необратимых не только 0. Для квадратных матриц n на n необратимы все матрицы A, у которых определитель =0, не только O - нулевая матрица, состоящая из одних нулей, а матрица -A существует для любой. То есть что там сложение, а что умножение - однозначно если две операции, о чём и писал
Это если у тебя группа и там только одна операция как в кубике Рубика и игре 15. Когда у тебя 2 операции (кольцо - гибрид двух групп на одном множестве в каком-то смысле, одна по умножению, другая по сложению то там однозначно что сложение, а что умножение.
Потому что там у тебя две бинарных операции, и два нейтральных элемента e1 для первой операции и e2 для другой
Но! По одной операции обратные для всех элементов a есть - тогда это сложение, элементы противоположными, а не обратными называют и обозначают (-a) вместо a^{-1} а по другой операции для обратимости есть исключение - у нейтрального элемента другой операции нет обратного.
То есть (-1)=-1 существует, а 0^{-1}= 1/0 не существует.
Иногда таких элементов необратимых не только 0. Для квадратных матриц n на n необратимы все матрицы A, у которых определитель =0, не только O - нулевая матрица, состоящая из одних нулей, а матрица -A существует для любой. То есть что там сложение, а что умножение - однозначно если две операции, о чём и писал
я не уверен, что смогу объяснить ребёнку про ассоциативностьзначит хреновый препод в отличие от меня
Вот тебе ассоциативность или сочетательное свойство умножения на примере как посчитать сколько маленьких кубиков в ящике 3 x 4 x 5
3 x (4 x 5) = (3 x 4) x 5
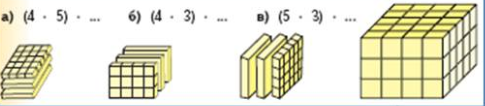
тут правда и коммутативность в этой иллюстрации тоже используется, но это уже детали
обобщенное умножение, которое композиция, и некоммутативно, и не обратимоесли брать композицию движений, то оно обратимо, и потому ещё меньше похоже на умножение натуральных чисел
короче запутаешь ты детей
А вот как умножить 2 яблока на 2 яблока?Собственно вот отсюда и видно, что операции на размерных величинах, это вообще-то не групповое сложение и умножение как тут многие написали, а умножение в алгебре. То есть умножение элементов поля(чисел) на объекты(векторы - наборы яблок).
И на самом деле два раза по два яблока это 2*(2*яблоко где * - операция отображающая пару (число, вектор) в вектор. И о перестановочности множителей тут речи нет в принципе. Она появляется только после того как воспользуешься подходящим изоморфизмом.
Конечно детям в начальной школе рассказывать это бессмысленно, но педагогика - на то и гуманитарная наука, что кроме вдалбливания выкладок напрямую там есть и хитрые психологические приемы, которые не математичны, но могут быть полезны. Их просто неправильно судить чисто с математической точки зрения.
Повторю ещё раз - процитированный кусок методички в первом посте таким приемом не является, это просто безграмотность авторши текста.
необратимость когда у нас 2 операции имеется в виду, 0^{-1} не существует, но (-1) существует . То есть сложение + обратимо, вычитать можешь всё, а умножение не всегда, делить на 0 не можешь
хотя бывают ослабления аксиоматики группы, часть аксиом выкидываем - полугруппы, моноиды и т.д. Не всегда есть обратимость даже на множестве с одной операцией. Мир многообразен. Но сложением такую операцию точно не называют, умножением иногда называют.
хотя бывают ослабления аксиоматики группы, часть аксиом выкидываем - полугруппы, моноиды и т.д. Не всегда есть обратимость даже на множестве с одной операцией. Мир многообразен. Но сложением такую операцию точно не называют, умножением иногда называют.
Если просто метаться от одного примера к другому, как ты делаешь сейчас, то кроме запутывания ничего и не выйдет.
А если последовательно обобщать термин от простых типичных примеров к общему определению, и потом применению в различных частных случаях - получится разумная теория.
А если последовательно обобщать термин от простых типичных примеров к общему определению, и потом применению в различных частных случаях - получится разумная теория.
мало что осталось от линала в голове, но помню:
что там вдалбливали теорию чисел и множеств и рассказывали какие операции и свойств у этих множеств может быть.
Наше принятое для счета множество: Евклидово (возможно не прав, не помню название)
Но существую и другие множества.
Скажем множество чисел M, в котором операция сложения определена как
Учитель не обозначил в какой Алгебре находятся эти числа , так что он прав
что там вдалбливали теорию чисел и множеств и рассказывали какие операции и свойств у этих множеств может быть.
Наше принятое для счета множество: Евклидово (возможно не прав, не помню название)
Но существую и другие множества.
Скажем множество чисел M, в котором операция сложения определена как
a+b = a^b
Учитель не обозначил в какой Алгебре находятся эти числа , так что он прав
ну да, только умножение чисел - в первом классе, а композицию функций - сильно позже
(я помнится в 5ом классе читал про функции, и не мог понять, что это - причём каждую конкретную в книжке понимал отлично, а вот абстракция была временно недоступна)
ну и я к чему всё?
что не найти столько крутых педагогов, чтоб всех детей способны были обучить всем предметам
овен нашёл своему сыну хорошую школу, допустим - и я не понимаю, почему он считает, что какая-то проблема у его конкретного ребёнка остаётся: путин не заставляет учить всех строго по этой методичке, хороший учитель всё равно учит хорошо; и если он особенно загоняется по математике, то он обучит сына основам математики сам
а школа должна предсказуемо работать в средней ситуации, когда отец хочет, чтоб сын в первую очередь рос сильным и здоровым мужиком, бил морды, ебал баб, верил в бога, не водился с пидорами; излишнее задротство по математике вредит всем этим пунктам, тут больше на спорт надо налегать
(я помнится в 5ом классе читал про функции, и не мог понять, что это - причём каждую конкретную в книжке понимал отлично, а вот абстракция была временно недоступна)
ну и я к чему всё?
что не найти столько крутых педагогов, чтоб всех детей способны были обучить всем предметам
овен нашёл своему сыну хорошую школу, допустим - и я не понимаю, почему он считает, что какая-то проблема у его конкретного ребёнка остаётся: путин не заставляет учить всех строго по этой методичке, хороший учитель всё равно учит хорошо; и если он особенно загоняется по математике, то он обучит сына основам математики сам
а школа должна предсказуемо работать в средней ситуации, когда отец хочет, чтоб сын в первую очередь рос сильным и здоровым мужиком, бил морды, ебал баб, верил в бога, не водился с пидорами; излишнее задротство по математике вредит всем этим пунктам, тут больше на спорт надо налегать
вот кстати выпускник мгу, а вы говорите что в первом классе что-то не так стали преподавать при путине
нашел в вики статью для интересующихся о чем я
http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%...
http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%...
Конечно детям в начальной школе рассказывать это бессмысленно, но педагогика - на то и гуманитарная наука, что кроме вдалбливания выкладок напрямую там есть и хитрые психологические приемы, которые не математичны, но могут быть полезны. Их просто неправильно судить чисто с математической точки зрения.да, но некоторые вещи надо просто вести к тому, чтобы они стали очевидными.
И самый треш происходит тогда, когда дети всё понимают, учитель понимает и нормально объяснил, и тут приходит методист, и говорит, что так излагать неправильно, потому что детям это не понятно.
Пример: старшая школа, физ-мат класс, математика: устоявшаяся традиция, при упрощении выражения вида x*y/x^2, зачёркивают x в числителе, двойку в знаменателе. Всем понятно, все этим оперируют как самим собой разумеющимся. Приходит методист, и делает выговор, то так нельзя, детям не смогут правильно понять математику так, надо обязательно расписать x*y/x*x и только потом вычёркивать "x". Это реальный пример из жизни (не моей, я в школе никогда не работал).
Учитель ещё может послать этих методистов. Хотя не всякий, если молодой учитель, то он куда больше зависим от администрации. Хуже, когда учитель подобным образом давит учеников. Увы, но это реальность советской (и современной российской) школы.
нашел в вики статью для интересующихся о чем я
*ссыль на теорию групп*
Я даже не знаю, какой из смайлов больше подходит.
нафиг иди, я матан на 5 сдал на физфаке
Жги дальше!
Я в таких случаях вижу задачу учителя (и родителя, если учитель не справляется) - проложить четкую границу между неправильным по существу и неправильным по соглашению. То есть ребенок должен понимать за что ему снижают оценку - за решение или за его оформление.
При этом я не считаю что снижение оценки за оформление - это однозначное зло. Там надо смотреть на реальные примеры. То есть за почерк например снижать оценку глупо, или за то, что человек умножил два числа в уме, а не расписал столбиком. А вот за то, что в том бардаке, которым обычно является запись решения задачи типичным школьником, отсутствует слово "Ответ" уже вполне можно(при условии что это обговаривалось заранее, разумеется). Хоть я и помню как бесили подобные придирки во время учебы.
При этом я не считаю что снижение оценки за оформление - это однозначное зло. Там надо смотреть на реальные примеры. То есть за почерк например снижать оценку глупо, или за то, что человек умножил два числа в уме, а не расписал столбиком. А вот за то, что в том бардаке, которым обычно является запись решения задачи типичным школьником, отсутствует слово "Ответ" уже вполне можно(при условии что это обговаривалось заранее, разумеется). Хоть я и помню как бесили подобные придирки во время учебы.
Какая связь между матаном и теорией групп? Или у вас на физфаке, как на экономе, "высшая математика"?
Собственно вот отсюда и видно, что операции на размерных величинах, это вообще-то не групповое сложение и умножение как тут многие написали, а умножение в алгебре. То есть умножение элементов поля(чисел) на объекты(векторы - наборы яблок).ну понеслось, третья операция, умножение элементов на числа, линейные-векторные пространства и алгебры
Конечно, матрицы можно складывать и умножать между собой, а можно умножать на числа. Что значит 2*A коректно, а A*2 нет? Это то же самое, если только у тебя числа не какой-нибудь изврат, когда x*y равно y*xЕсли есть две операции a+b для векторов и умножение на числа 5a например, то это линейн пр-во, если еще вектора между собой перемножаются - алгебра, как алгебра матриц.
Размерные величины это другое - градуированые алгебры - нет разве?
Как это 5км/ч*3ч можно умножать, а наоборот 3ч*5км/ч нет? Приплыли.
Как же ты полиномы-то перемножаешь от одной или многих переменных (5x^2+3y)*(7x-2y с чего это там сомножители-то нельзя переставлять местами?
Нельзя переставлять - получим разный результат если только числа (коэффициенты) не коммутируют, или переменные когда их не одна, как в матрицах например когда
5X*3Y^2 не равно 3Y^2 * 5X если матрицы не коммутируют, потому что для матриц XY вообще говоря не равно YX
а чего это 2кусок/чашка * 5чашка не равно 5чашка * 2кусок/чашка
И не квадратные яблоки, а яблоко в квадрате можно определить как метр^2, только смысла это делать с яблоками нет, а с метрами есть для измерения площади
Размерные величины перестановочны. Те коммутируют
По поводу методики что учитель должен писать сомножители в определенном порядке когда вводят умножение вводят согласен с тобой, и какой множитель в каких странах первый зависит от специфики, некоторые справа налево или сверху вниз пишут или считают по-другому в другом языке. У нас 2 куска на первое место ставят, а в других странах наоборот. А от ученика это требовать нельзя, если учитель поговорил и выяснил, что это он такой продвинутый, что у него переместительный закон в подсознании уже. А если ученик просто совсем тупой и не понимает усмножение вообще, то может и надо требовать в определенном порядке писать
Дома умному ученику есть повод объяснить что все ошибаются и учитель тоже, и повод сказать, что он не для отметок учится. Или коллекционировать учительские маразмы чтобы принять потом меры они пригодятся при переводе к другому учителю или чтобы этого убрали, при переходе в другую школу и т.д.
Скорее, не у "вас", а у него.
можно про идеальных учителей поговорить, но где их взять, да ещё в таком количестве?
Поле "ответ", это, допустим, святое: потому что есть решение, разными способами может быть получено, это как рассуждения, но итоговый краткий и чёткий ответ должен быть дан.
Но я чётко помню, как школьные учителя требовали оформлять физику: там рисуется 3 столбика, в одном условие, во втором формулы, в третьем решение, снизу ответ. Жутко неудобная вещь, с которой я постоянно пытался воевать. Но для физичек это какая-то религия. И каким было облегчение, когда я попал в нормальную школу к нормальным физикам, которым эта форма была дика, и они смотрели на обоснование решения, а уж никак не на оформление.
Увы, но в школах треш творится. И это не результат правления Путина, и не результат реформ Гайдара. Оно идёт ещё со времён СССР, от тех самых советских учителей, на которых многие дрочат. Совок умер, система осталась.
Поле "ответ", это, допустим, святое: потому что есть решение, разными способами может быть получено, это как рассуждения, но итоговый краткий и чёткий ответ должен быть дан.
Но я чётко помню, как школьные учителя требовали оформлять физику: там рисуется 3 столбика, в одном условие, во втором формулы, в третьем решение, снизу ответ. Жутко неудобная вещь, с которой я постоянно пытался воевать. Но для физичек это какая-то религия. И каким было облегчение, когда я попал в нормальную школу к нормальным физикам, которым эта форма была дика, и они смотрели на обоснование решения, а уж никак не на оформление.
Увы, но в школах треш творится. И это не результат правления Путина, и не результат реформ Гайдара. Оно идёт ещё со времён СССР, от тех самых советских учителей, на которых многие дрочат. Совок умер, система осталась.
А если ученик просто совсем тупой и не понимает умножение вообще, то может и надо требовать в определенном порядке писатьнет, тогда надо требовать, чтобы он разобрался с умножением. В противном случае он так и будет тупо подставлять числа в формулу, не понимая сути, и непонимание будет только расти и расти. В этом и проблема, что всё построено так, чтобы ученик что-то запомнил, а не научился что-то понимать.
Славно вбросил гойчегар угля на вентиляторЪ. Эт я про знаменитую проблемму умножения 14 на 88 9 на 2.
Зогбавно чейтать гуманитариев истерящих про наступление релятивизьма и прочие ужосы.
Вопче-то операция умножения в математике может быть определена как a*b = b*a так и как a*b =/= b*a.
Лично мне да и однокурсникам вышколенным на то, что от перестановок слагаемых произведение не меняется не без запинок сдавались тензоры и операторы с функционалами, где как раз порядок слагаемых - важный момент.
Никакого ужоса постмодерна тут нет, просто прусская гимназия на уроках арифметики готовила будущих артиллеристов и военных инженеров, оттого и прошивали им на подкорки соответствующую версию математики, сейчас нужны другие профессие оперирующие с другим, вот и водят чуть другую, но всё таки вполне кошерную математику.
При обсуждениях проблеммы 2*9/9*2 выплывает всё больше интересного.
1) оказываецо подобная форма оформления решений, где размерность по первому множителю была в дореволюционных учебнегах, и в программе совшколы до 38 года - о как! получаецо, что те люди, которые проектировали Катюши, Т-34 и Спутник с прочим Космосом учились по книгам, где размерность по первому множителю, а вот Горбачёв и Ельцин, по тем, где от перестановки мест ...
2) ещё такой мо-ментик: а ведь коммутативность - это одно из самых постмодернистских свойств. Нуачö - переставляй, умножай, еби гусей! Порядок слягаемых (иерархия, однако) неважен. Хо-хо, а впряглиась защищать коммутативность как раз постмоденохулы.
3) А ведь если оглянуться (весьма забавно, коммуникативофилы ратуют за абстрактное мышление и нешаблонность, а сами то окажецо, что коммуникативность - это эвойство мира идей, а вот реальность данная нам на раёне сплошь некоммуникативна: американец в Китае - это не китаец в Штатах, горожанен на деревне - совсем не то, что селюк в городе. Да и классег ведь писал: "Прошай, некоммунитативная Россия, ..."
Кстати, а ведь реально хорошее название для партии социального аппартеида.
1) оказываецо подобная форма оформления решений, где размерность по первому множителю была в дореволюционных учебнегах, и в программе совшколы до 38 года - о как! получаецо, что те люди, которые проектировали Катюши, Т-34 и Спутник с прочим Космосом учились по книгам, где размерность по первому множителю, а вот Горбачёв и Ельцин, по тем, где от перестановки мест ...
1) оказываецо подобная форма оформления решений, где размерность по первому множителю была в дореволюционных учебнегах, и в программе совшколы до 38 года - о как! получаецо, что те люди, которые проектировали Катюши, Т-34 и Спутник с прочим Космосом учились по книгам, где размерность по первому множителю, а вот Горбачёв и Ельцин, по тем, где от перестановки мест ...Я бы понял, если бы это вытащил Пофи, но ты...
тебя слаер укусил, зачем дислексиков копипастишь?
Чо, идеологически неверные спекуляции постить не следует, не к лицу?
Этого конкретного дислексика я всё время же копипастил. По-хорошему, конечно, надо было просто его мысль пересказать, но мне, конечно же, было лень.
Я бы понял, если бы это вытащил Пофи, но ты...Так он не меньший тоталитарист, просто с другими идеями.
Потому что вокруг многовато гандонов, очевидно.большинство которых - результат совеццкого(tm "качественного" образования, на которое ты так дрочишь?
где же вышла осечка?
ты кстати сам тот еще рашкован и гандон, штраф то за А-полосу заплатил?
или твой либерализм-попзиционизм заканчивается там где перестает быть удобным/выгодным?
У них в начальной школе ещё и некоммутативность сложения, в задачах типа "на ветке сидело 3 птицы, потом к ним ещё 2 прилетели и сели на ветку" тоже требуют на первое место ставить слагаемое кто сидел на ветке.чтобы через 10 лет на мех-мате каждую херь абелевой группой не называть. в зародыше готовят к подозрениям.
к сожалению, среди школьных учителей математики хороших математиков не так много.
кто только слева писать умеет, кто про Иисуса Христа рассказывает. а кто-то предложит в арифметических примерах все числа прописью писать: "четыре плюс два равно шесть"
надо математику религией объявлять и запрещать профессионалам типа белошистой пользоваться математическими знаками, потому что это кощунство и разжигание ненависти.
можно про идеальных учителей поговорить, но где их взять, да ещё в таком количестве?Роботы + дистанционное обучение?
Индивидуально программа чередует мультик с объяснением темы и решением примеров с автоматической проверкой ответа. Если слишком много неправильных ответов, уровень начинается сначала. Каждый проходит в своем темпе. Тем, кто проходит быстро, открываются бонусные уровни в виде "нестандартных" заданий с разных олимпиад.
Плюс набивание решений задач с отсылкой на проверку хорошим учителям.
На уроках же с реальным учителем (чтобы не совсем асоциально) вопросы учеников, придумывание собственных задач, устный опрос, вызовы к доске, + развлекуха в виде оффлайн игр/соревнований, в том числе командных.
Какая связь между матаном и теорией групп? Или у вас на физфаке, как на экономе, "высшая математика"?зато для него конденсатор - это не просто две палочки, значок параллельности прямых, про которые евклид в рекламе зануси доказал, что они не пересекаются.
на самом деле не хорошо тут смеяться. у мех-мата еще то понимание физики.
Так он не меньший тоталитарист
Что точно понятно, так это что ты не меньший дебил чем он
зато для него конденсатор - это не просто две палочки, значок параллельности прямых, про которые евклид в рекламе зануси доказал, что они не пересекаются.Конденсаторы в школе проходятся, на физфаке учиться необязательно, чтобы знать обозначение
Кстати, не факт, что твоё утверждение вообще верно.
Я бы понял, если бы это вытащил Пофи, но ты...Толстый тролль тащить жырь въ тредь.
у мех-мата еще то понимание физики.на мехмате физику преподы с физфака дают примерно так же, как в моей истории выше про мою школу
за исключением того, что ставят 4 и 5, а не 2 и 3-, если ничего не понял
рада снова читать тебя на флокале
я сейчас как раз в процессе войны смучительницей нач.классов.
я ей предлагала почитать вот эту статью хотя бы:
"Учителя большого города: Николай Константинов
Почему в младших классах прививают ненависть к математике, как определить, чем склонен заниматься ребенок, и чем так важна компания"
у меня вопрос. ты очень хорошо излагаешь мысль в 4-х постах, нет ли у тебя написанной статьи на эту тему?
я сейчас как раз в процессе войны с
я ей предлагала почитать вот эту статью хотя бы:
"Учителя большого города: Николай Константинов
Почему в младших классах прививают ненависть к математике, как определить, чем склонен заниматься ребенок, и чем так важна компания"
у меня вопрос. ты очень хорошо излагаешь мысль в 4-х постах, нет ли у тебя написанной статьи на эту тему?
а чо, в рашке физика уже с 5го класса?
В каком классе в России начинают изучать физику? В общем случае зависит от программы. У моих знакомых ребёнок начал учить в шестом, на пятом году обучения.
все верно
математика в начальной школе - прикладная. в пятом классе дети начнут учить физику, где узнают про размерности, и математику, где узнают про коммутативность
но было бы хорошо, чтобы к тому моменту у них было нормальное понимание, почему мы умножаем 2 на 9
к сожалению, очень многие дети просто тупо из таких задач запоминают правило "если есть два числа, умножить их друг на друга". в физике такая хуета оборачивается большими проблемами
родители, объясните своим детям, в чем тут прикол, и они нормально переживут ужасы школы
математика в начальной школе - прикладная. в пятом классе дети начнут учить физику, где узнают про размерности, и математику, где узнают про коммутативность
но было бы хорошо, чтобы к тому моменту у них было нормальное понимание, почему мы умножаем 2 на 9
к сожалению, очень многие дети просто тупо из таких задач запоминают правило "если есть два числа, умножить их друг на друга". в физике такая хуета оборачивается большими проблемами
родители, объясните своим детям, в чем тут прикол, и они нормально переживут ужасы школы
к сожалению, очень многие дети просто тупо из таких задач запоминают правило "если есть два числа, умножить их друг на друга". в физике такая хуета оборачивается большими проблемамиА, собственно, как надо действовать, если "есть два числа"?
...
родители, объясните своим детям, в чем тут прикол, и они нормально переживут ужасы школы
Мне всегда казалось, что числа - на то и числа, чтобы быть безразмерными (и меня задалбывал геометр, выпускник ФФ кстати, который обожал везде в геометрии лепить размерности).
Вообще, не помню в физике проблемы "число-размерность" - ответ считали всегда формулой, и только потом подставляли цифры, без формулы ответ не считался ответом. Или теперь считается, что не надо выводить формулу в ответ? (как тогда считать погрешность в случае эксперимента?)
А, собственно, как надо действовать, если "есть два числа"?А в задаче не числа, а физические объекты.
Мне всегда казалось, что числа - на то и числа, чтобы быть безразмерными (и меня задалбывал геометр, выпускник ФФ кстати, который обожал везде в геометрии лепить размерности).
вернёмся к нашим баранам, т.е. к теме треда ака коммутативности - я не пойму - они что не коммутируют? Тензора что ли или операторы? нет этого в школе - в чём проблема переставить сомножители хоть и размерные местами? Или (я не сильно следил за последнее время за тредом) и речь о другом?
Числа коммутируют.
Но из этого автоматически не следует ответ на вопрос о том, какправильно нужно можно преподавать.
Но из этого автоматически не следует ответ на вопрос о том, как
Ну да. Но моего сына бесило. Просил в другую школу перевести или хотя бы к другому учителю не такому некоммутативному методисту-ортодоксу. Я сказал забей, в старшей школе нет этого маразма.
Но там есть свой.
Эта программа сейчас Школы России имхо называется. Очередное поколение ортодоксов-недоучек мучит очередное поколение школьников и учителей для них.
Но там есть свой.
Эта программа сейчас Школы России имхо называется. Очередное поколение ортодоксов-недоучек мучит очередное поколение школьников и учителей для них.
не такому некоммутативному методисту-ортодоксу.Ну да, ещё и может быть учитель-мудак, что довольно вероятно. Но это даже уже третий вопрос.
Очередное поколение ортодоксов-недоучек мучит очередное поколение школьников и учителей для них.Ну наверное как-то так. Учителя не понимают почему и зачем, ученики тем более. Сами авторы методички может, и понимают эту идею, но в методичке нормально объяснить не могут. В итоге, скорее всего, лучше было бы, если бы на эту идею забить, и делать как есть. (А "как есть" — это не обращать внимания на порядок множителей, судя по общественному возмущению, все так учились).
Но тут тоже вопрос — а что значит "лучше" и для кого именно.
Для умных лучше. Для послушных в дальнейшем режиму - нет
я про РФ если чо, в других странах свои тараканы
я про РФ если чо, в других странах свои тараканы
Для умных лучше. Для послушных в дальнейшем режиму - нетНо ведь даже и это не очевидно. То есть если "неправильный" ответ зачёркивается на основании "потому что учитель так сказал", то да (а изначальная картинка запустившая срач в рунете выглядела именно так для всех а если есть другие аргументы, то может как раз наоборот.
В этом треде приводились уже различные аргументы, про дисциплину ума, дисциплину оформления (и что это нужно для решения сложных задач потом, а не для тупого выполнения приказов про то коммутативность умножения — это просто некое вовсе необязательное свойство операции к данной конкретной задаче отношения не имеющее и тд, ни к чему их повторять.
PS Если моё мнение интересно, то я кагбэ не знаю как лучше и как надо, сам не очень помню как и что я в то время думал, а детей таких не учил. Но мне странно, что все остальный точно знают Единственный Ответ Как Правильно Учить, и вообще что это такой срач вызвало в сети вообще и у нас тут в частности.
Но мне странно, что все остальный точно знают Единственный Ответ Как Правильно Учитьнет, тут всё проще.
многие здесь пытаются найти какое-то обоснование методики... Вот моё мнение, не стоит пытаться понять логику идиота, а уж тем более, выискивать в ней здравое зерно. Нет там логики. Кто не умеет учить — тот учит тому, как учить. Вот и весь принцип. Примерно как чиновникам нужно показать свою полезность, и для этого часто придумывают тонны лишних бумажек, без которых никак, так и таким тёткам, нужно как-то себя проявлять, и поэтому они плодят все эти методологии. В результате, только мешают другим.
В данном случае просто очевидный бред. Бывает ещё и не такой очевидный, но всё равно бред.
Вот моё мнение, не стоит пытаться понять логику идиота, а уж тем более, выискивать в ней здравое зерно. Нет там логики.Ну ты сам же удивлялся, что не только идиоты про это думают:
Самое интересное, я когда-то наблюдал, что подобные концепции защищала, например, мамашка, с очень серьёзным математическим образованием, и довольно хорошим аналитическим мышлением. Не в такой дикой форме, конечно.Кроме того, оказывается до революции действительно так преподавали в школах (тут наверное правда нужно будет получше ссылку найти если не веришь). Ну и другие люди тоже видят какие могут быть аргументы за это: альфа, например.
Странно что после этого ты заявляешь, что "да это просто-напросто бред идиота, что вы тут обсуждаете". Может быть конкретная инициатива Белошистой — действительно бред идиота (этого я не знаю, так как к ней в голову залезть не могу, а мотивация у неё разная могла быть, как бредовая, так и что-то из серии, что тут в треде обсуждали но в принципе какая разница, что именно думает она, обсуждается тут сама идея, а не то, почему она её сторонник.
Работая в школе, я видела сколько угодно случаев преобладания методики над здравым смыслом и пониманием конкретного ученика. И, к сожалению, видела очень мало обратного - когда учитель реально мог показать преимущества строгого следования методике (это приводит меня к мысли, что на самом-то деле преимущества очень призрачные и скорее считающиеся, чем реальные, т.е. некий общеприняты миф, который не принято подвергать сомнению). Мне лично приходилось отстаивать право своих учеников на обучение не в строгом соответствии с методикой, а в соответствии с их способностями и пониманием предмета Нервов на это пришлось положить - мама не горюй. И я с тех пор довольно скептически отношусь к подобным формальным методикам (в отличие от многих других, коих в преподавании полно)
Нервов на это пришлось положить - мама не горюй. И я с тех пор довольно скептически отношусь к подобным формальным методикам (в отличие от многих других, коих в преподавании полно)В-третьих, многие форумчане правильно заострили внимание на том, что в школе не даётся понятие размерности и безразмерных величин. Во всяком случае, не даётся до пятого класса, когда начинается физика.Да вообще-то и после сдачи школьного курса физики и получения диплома университета люди умудряются не знать, что такое киловатт-час.
(А "как есть" — это не обращать внимания на порядок множителей, судя по общественному возмущению, все так учились).где-то в районе первого-второго класса, когда училась таблица умножения, учитель просто показал, что умножение коммутативно
И заодно потом вплоть до пятого класса давали приёмы устного счёта, коммутативные, ассоциативные и дистрибутивные. Народ особо не понимал, но юзал с удовольствием. С неменьшим удовольствием я в пятом классе обнаружил доказательсва используемых приёмов.Имхо, математическая магия - это отличный завлекательный приём. Тут вот уже вспоминали пятнашки
киловатт-час.ну да ладно, догадаться по размерности не трудно. На форуме вот периодически мелькают киловатты, делённые на часы, а это уже, видимо, что-то из курса высшего образования
Давеча давала открытый урок. Ну, опозорилась, как всегда, но дело даже не в том.
Одна из основных претензий, которые мне высказали и и представители методического центра, и учителя из этой же школы - нужно говорить не "поделить", а "разделить".
Причем высказывалась это в форме, что "это кто вообще и как ее пустили преподавать? она даже говорить не умеет. Ааа, НЕ ПЕДАГОГ".
При этом мы имеем средний балл по ЕГЭ по математике 54 (по Москве средний примерно такой же).
Одна из основных претензий, которые мне высказали и и представители методического центра, и учителя из этой же школы - нужно говорить не "поделить", а "разделить".
Причем высказывалась это в форме, что "это кто вообще и как ее пустили преподавать? она даже говорить не умеет. Ааа, НЕ ПЕДАГОГ".
При этом мы имеем средний балл по ЕГЭ по математике 54 (по Москве средний примерно такой же).
задал своему сыну, дошкольнику, задачу про сахар и чашки, правда чашек взял поменьше - 5 штук
Начнем с того, что он в принципе самостоятельно не смог решить эту задачу. Пытался что-то считать на пальцах, но выходило 12 кусков или 11 или 9. Тогда я начал упрощать и взял 2 чашки, тут он легко справился. Затем три, затем четыре и наконец пять. Мгновенно получился правильный ответ. На вопрос, как ты посчитал, он толком ответить не смог, но сказал, что типа понял, что надо прибавлять два каждый раз. То есть немного позаниматься и он поймет, что надо просто сложить пять раз по два. Сейчас пока он складывает не более двух чисел за раз. С другой стороны ему совершенно понятна фраза "5 раз по 2 куска сахара" или "2 куска сахара 5 раз", это не вызывает у него никакого непонимания, хотя сколько это будет, как я уже писал, он сказать и даже посчитать не может. Это я к тому, что сама операция умножения понятна на примитивном уровне даже дошкольнику, хотя он и не может представить ее в виде суммы и вычислить. Вопрос, насколько надо разжевывать, что умножение представимо в виде суммы, до зубрения таблицы умножения лично для меня теперь совершенно не очевиден. Просто я вижу, что дети очень легко запоминают, но не всегда легко понимают.
Что касается записи 5*2 или 2*5, то если изначально какое-либо соглашение было озвучено, то придерживаться его, безусловно, ученик должен, однако снижать оценку за нарушение этого соглашения существенным образом нельзя, на мой взгляд, достаточно поставить к оценке минус. Подчеркну, именно соглашение, а не навязанное правило. Ребенку надо сказать, что писать можно и по-другому, но давайте мы с вами примем решение писать именно так.
И, да, из меня методист никакой
Начнем с того, что он в принципе самостоятельно не смог решить эту задачу. Пытался что-то считать на пальцах, но выходило 12 кусков или 11 или 9
. Тогда я начал упрощать и взял 2 чашки, тут он легко справился. Затем три, затем четыре и наконец пять. Мгновенно получился правильный ответ. На вопрос, как ты посчитал, он толком ответить не смог, но сказал, что типа понял, что надо прибавлять два каждый раз. То есть немного позаниматься и он поймет, что надо просто сложить пять раз по два. Сейчас пока он складывает не более двух чисел за раз. С другой стороны ему совершенно понятна фраза "5 раз по 2 куска сахара" или "2 куска сахара 5 раз", это не вызывает у него никакого непонимания, хотя сколько это будет, как я уже писал, он сказать и даже посчитать не может. Это я к тому, что сама операция умножения понятна на примитивном уровне даже дошкольнику, хотя он и не может представить ее в виде суммы и вычислить. Вопрос, насколько надо разжевывать, что умножение представимо в виде суммы, до зубрения таблицы умножения лично для меня теперь совершенно не очевиден. Просто я вижу, что дети очень легко запоминают, но не всегда легко понимают.Что касается записи 5*2 или 2*5, то если изначально какое-либо соглашение было озвучено, то придерживаться его, безусловно, ученик должен, однако снижать оценку за нарушение этого соглашения существенным образом нельзя, на мой взгляд, достаточно поставить к оценке минус. Подчеркну, именно соглашение, а не навязанное правило. Ребенку надо сказать, что писать можно и по-другому, но давайте мы с вами примем решение писать именно так.
И, да, из меня методист никакой
Что касается записи 5*2 или 2*5, то если изначально какое-либо соглашение было озвучено, то придерживаться его, безусловно, ученик должен, однако снижать оценку за нарушение этого соглашения существенным образом нельзя, на мой взгляд, достаточно поставить к оценке минус.
Вот уж от тебя такого не ожидал.
То есть дальше ты уже не смог прочитать?
конечно, я никогда не дочитываю до конца.
ИМХО, идиотизм хоть на йоту, хоть на миллиметр оправдывать это "правило".
ИМХО, идиотизм хоть на йоту, хоть на миллиметр оправдывать это "правило".
конечно, я никогда не дочитываю до конца.Сделай исключение, дочитай до конца, пожалуйста.
ИМХО, идиотизм хоть на йоту, хоть на миллиметр оправдывать это "правило".
методист из тебя никакой. и?
ты ж мнение-то высказываешь тем не менее. я удивлен, что оно у тебя такое.
ты ж мнение-то высказываешь тем не менее. я удивлен, что оно у тебя такое.
Псесиально для тебя выложу еще раз то, что тебе следует прочитать внимательно от начал и до конца, чтобы не выпадали никакие части текста. Надеюсь, ты сможешь с этим справиться. И, на всякий случай, выделю некоторые места жирным шрифтом.
Что касается записи 5*2 или 2*5, то если изначально какое-либо соглашение было озвучено, то придерживаться его, безусловно, ученик должен, однако снижать оценку за нарушение этого соглашения существенным образом нельзя, на мой взгляд, достаточно поставить к оценке минус. Подчеркну, именно соглашение, а не навязанное правило. Ребенку надо сказать, что писать можно и по-другому, но давайте мы с вами примем решение писать именно так.
может лучше вообще отказаться от нотации *, чтобы проблем не было?
Записывать что-нибудь вроде sum $ [1..6] >> [2] , хоть символов и больше, зато весь процесс в деталях описан
Записывать что-нибудь вроде sum $ [1..6] >> [2] , хоть символов и больше, зато весь процесс в деталях описан
Подчеркну, именно соглашение, а не навязанное правило. Ребенку надо сказать, что писать можно и по-другому, но давайте мы с вами примем решение писать именно так.ну ты красава, сарказм прям зашкалил. там со стула не упал часом?
что именно такого важного написано в этом куске, выделенном жирным? Ты предлагаешь СОГЛАШЕНИЕ писать 2*9, а не 9*2. Чтобы ребенок помнил о какой-то хуете, соглашении - какой множитель ставить на какое место. Но типа писать можно и наоборот, но ты не пиши. Какой в этом вообще смысл? С моей точки зрения это дикость. Я бы подошел к учителю математики и попробовал бы договориться с ней не акцентировать внимание на порядке множителей. А ребенку бы сказал, чтобы писал как захочет - в конечном счете на оценки в школе пох, тут лучше, чтобы у самого ребенка правильное понимание было.
и самое смешное будет, когда уравнения пойдут. Когда ребенок напишет 2х, а надо было, видите ли писать х*2.
или даже круче - вместо 2х+3у=15 надо было писать у*3+2х=15 - порядок же в сложении тоже дико важен.
или даже круче - вместо 2х+3у=15 надо было писать у*3+2х=15 - порядок же в сложении тоже дико важен.
Какой-то ненулевой смысл в этом есть.
Ребенку вообще регулярно приходится запоминать некие соглашения. Почему правило правой руки, а не левой, например? Почему после некоторых сокращений точка ставится, а после некоторых - нет?
Так что с методической точки зрения это может быть, например, введено с дисциплинирующими целями... Хотя зачем это я пишу, в теме масса объяснений звучало (и это в том числе но ты ж их не прочел.
Впрочем, этот смысл существовал для тех, кто учил Белошистскую (или для тех, кто учил тех, кто учил ее, или... а для нее уже потерян, судя по тексту.
Ребенку вообще регулярно приходится запоминать некие соглашения. Почему правило правой руки, а не левой, например? Почему после некоторых сокращений точка ставится, а после некоторых - нет?
Так что с методической точки зрения это может быть, например, введено с дисциплинирующими целями... Хотя зачем это я пишу, в теме масса объяснений звучало (и это в том числе но ты ж их не прочел.
Впрочем, этот смысл существовал для тех, кто учил Белошистскую (или для тех, кто учил тех, кто учил ее, или... а для нее уже потерян, судя по тексту.
Ты вот вроде не ребенок, но всю мысль целиком уловить не можешь.
Давай разжую.
1. Ребенку надо сказать, что писать можно и так и так, потому что это правда.
2. Ребенку стоит предложить подумать, как ему больше нравиться писать и почему, предложить свой вариант.
3. С ребенком стоит заключить соглашение, что пишем так или иначе.
4. Это процесс в том числе позволит ребенку понять, почему можно писать и так и так.
5. Определенная договоренность позволит учителю определять, правильно ли ученик понял задачу и решил ее.
6. Родительское "делай как хочешь, потому что учитель мудак" не пойдет на пользу ребенку.
7. Так или иначе ребенок запоминает и выполняет множество формальных правил, которые ему вообще никак не объясняются, поэтому выполнение соглашения, с которым сам ребенок осознанно согласился, ему не навредит.
8. Я категорически против, что ребенку безопеляционно говорили, что писать правильно так, а не иначе, если это на самом деле не так.
9. Я категорически не приемлю то объяснение, что дано в методичке.
10. самодурство учителей ровно настолько же плохо, как и самодурство родителей.
Давай разжую.
1. Ребенку надо сказать, что писать можно и так и так, потому что это правда.
2. Ребенку стоит предложить подумать, как ему больше нравиться писать и почему, предложить свой вариант.
3. С ребенком стоит заключить соглашение, что пишем так или иначе.
4. Это процесс в том числе позволит ребенку понять, почему можно писать и так и так.
5. Определенная договоренность позволит учителю определять, правильно ли ученик понял задачу и решил ее.
6. Родительское "делай как хочешь, потому что учитель мудак" не пойдет на пользу ребенку.
7. Так или иначе ребенок запоминает и выполняет множество формальных правил, которые ему вообще никак не объясняются, поэтому выполнение соглашения, с которым сам ребенок осознанно согласился, ему не навредит.
8. Я категорически против, что ребенку безопеляционно говорили, что писать правильно так, а не иначе, если это на самом деле не так.
9. Я категорически не приемлю то объяснение, что дано в методичке.
10. самодурство учителей ровно настолько же плохо, как и самодурство родителей.
ребенок выполняет множество формальных правил, за которыми стоит СМЫСЛ. про правило правой и левой руки, например, у оратора выше - если ты неправильно запомнил, правило какой именно руки, тогда ты неверно решишь задачу.
в случае же данного правила - оно не несет никакой смысловой нагрузки и не приводит к неправильному решению задачи в случае его нарушения. оно тупо забивает мозг ребенку ненужной информацией. более того, поскольку ребенок маленький - он вообще может не понять твоих объяснений "почему делать можно и так и так, но делать нужно именно так".
И да, у меня четкое ощущение, что я здесь зря трачу время, поскольку, очевидно, ты относишься предвзято к моим словам. Ты придумал правило - все что говорит вован - чушь, и следуешь ему. Твоя тональность, сарказм, все вот это "давай тебе разжую" вынуждает со спокойной совестью послать тебя куда подальше и закрыть разговор.
в случае же данного правила - оно не несет никакой смысловой нагрузки и не приводит к неправильному решению задачи в случае его нарушения. оно тупо забивает мозг ребенку ненужной информацией. более того, поскольку ребенок маленький - он вообще может не понять твоих объяснений "почему делать можно и так и так, но делать нужно именно так".
И да, у меня четкое ощущение, что я здесь зря трачу время, поскольку, очевидно, ты относишься предвзято к моим словам. Ты придумал правило - все что говорит вован - чушь, и следуешь ему. Твоя тональность, сарказм, все вот это "давай тебе разжую" вынуждает со спокойной совестью послать тебя куда подальше и закрыть разговор.
оно не несет никакой смысловой нагрузки
Может нести.
не приводит к неправильному решению задачи
Не приводит к неправильному ответу. Правильное ли решение — зависит от того, что по договорённости означает такая запись.
оно тупо забивает мозг ребенку ненужной информацией
В данном случае именно коммутативность умножения является дополнительной информацией, которая к задаче отношения не имеет.
И да, у меня четкое ощущение, что я здесь зря трачу время, поскольку, очевидно, ты относишься предвзято к моим словам. Ты придумал правило - все что говорит вован - чушь, и следуешь ему. Твоя тональность, сарказм, все вот это "давай тебе разжую" вынуждает со спокойной совестью послать тебя куда подальше и закрыть разговор.Странно, что ты обижаешься на стиль общения в форуме. Но мне не трудно от него отказаться.
Безусловно, я не считаю, что все, что ты говоришь, чушь. Впрочем, ровно такой же упрек можно было бы сделать и тебе, про твой комментарий в стиле "это идиотизм". Но это не имеет отношения к существу.
Соглашение, а не правило, не обязано нести смысловой нагрузки. Зато следование ему позволяет оценить, понимает ли ученик задачу. Ведь если вы с учениками договорились сначала писать сахар, а потом разы, то ученик, написавший наоборот, вероятно не совсем понял задачу и с ним следует позаниматься еще чуть больше других. Ты, мне кажется, путаешь математику как науку с процессом обучения. Еще раз подчеркну, я не говорю, что так делать надо обязательно, я говорю, что это допустимо пи определенных условиях. К таким условиям я отношу совместное соглашение, но не навязывание в соответствии с той методичкой.
ты пишешь - "соглашение не обязано нести смысловой нагрузки". а тогда какую нагрузку должно нести соглашение? я еще могу понять некие мненонические штуки для запоминания каких-то сложных формул. Также понятно, условно, что можно писать Е=mc^2, а можно написать и наоборот или E=cmc, но проще (ДЛЯ ЗАПОМИНАНИЯ) именно первый вариант.
Насчет понимания, правильно ли решил ученик задачу - ок, объясни мне, что тут вообще можно не понять
Ну ладно там сложная задачка, но здесь-то одно всего действие, какое понимание? И что ты будешь делать, когда тебе зачеркнут 2х+3у и напишут у*3+2х - как ты здесь ребенку будешь объяснять про "соглашения"?
Насчет понимания, правильно ли решил ученик задачу - ок, объясни мне, что тут вообще можно не понять
Ну ладно там сложная задачка, но здесь-то одно всего действие, какое понимание? И что ты будешь делать, когда тебе зачеркнут 2х+3у и напишут у*3+2х - как ты здесь ребенку будешь объяснять про "соглашения"?Более того, пока не доказана коммутативность умножения для натуральных чисел, рановато вводить коммутативное умножение.
Можно ввести пару знаков >*> и <*< и использовать их для разного порядка умножения. А потом в качестве триумфа математической науки ввести *, доказав ассоциативность операции.
Можно ввести пару знаков >*> и <*< и использовать их для разного порядка умножения. А потом в качестве триумфа математической науки ввести *, доказав ассоциативность операции.
И что ты будешь делать, когда тебе зачеркнут 2х+3у и напишут у*3+2х - как ты здесь ребенку будешь объяснять про "соглашения"?попрошу ребёнка доказать эквивалентность. Если не сможет - то скажу не выделываться.
Понимаешь, даже если дать ребёнку пару дюжин груш и разрешить раскладывать в любом порядке, коммутативность умножения для любого натурального числа так не докажешь. Хотя сомнения, конечно, могут закрасться. Вот когда он сам сможет сформулировать их - тогда можно и намекнуть на доказательства.
Ну заодно можно рассказать про "не верь глазам своим" и показать гифку и бесконечной шоколадкой.
P.S. Я сам начал пользоваться интегралами Римана для решения задач по физике только тогда, когда был уверен, что если меня призовут к доске, то я смогу вывести всю необходимую теорию, начиная от школьных понятий о рядах
И что ты будешь делать, когда тебе зачеркнут 2х+3у и напишут у*3+2х - как ты здесь ребенку будешь объяснять про "соглашения"?Он будет решать проблемы по мере поступления
Для начала лично я познакомилась бы с таким учителем, так как пока такие мне не встречались. Не думаю, что логика "Сегодня ты играешь джаз, а завтра родину продашь" должна тут использоватьсяВ данном случае именно коммутативность умножения является дополнительной информацией, которая к задаче отношения не имеет.Ну это уже вообще ЛОЛ. Ага, давайте детей (всех скопом) заранее готовить, что есть и некоммутативное умножение. В стране, где 75% умножают на калькуляторе однозначные числа. Ты им еще про группы с кольцами объясни. Да наоборот, надо сразу вбить в голову, что умножение коммутативно, как и сложение - ну это же гораздо проще. Потом, если у ребенка способности к математике, он уже сам в ВУЗе (а раньше это просто не изучают) сможет понять, что априори это не так.
Честно говоря, я этот тред сначала даже и читать не стал, думал тут 5 страниц обсирания этой дуры, как там ее фамилия - не упомню. Но когда прочитал - да, я офигел, что тут еще и базу некую под правильность (частичную) этого подвели. Блин, это дети, маленькие, ну проще же надо быть.
В стране, где 75% умножают на калькуляторе однозначные числа.75% статистики берется с потолка.
Более того, пока не доказана коммутативность умножения для натуральных чисел, рановато вводить коммутативное умножение.я очень надеюсь, что это тонкий стеб уже пошел.
Больше не смог ни до чего в тексте докопаться, я так понял? Не понял, что 75% - это условная цифра, не имеющая отношения к теме вопроса? Надо было написать "бОльшая половина", видимо, но нет, ты бы и здесь нашел что ответить, уверен, что половина не бывает большей или меньшей. Даже странно, ты вроде сам начал эту тему, вроде сам охреневал, что же случилось-то с тобой?
я очень надеюсь, что это тонкий стеб уже пошел.ну приведи доказательства, если всё так просто. По факту дети до таблицы умножения так уж точно проходят не операцию "умножение", а операцию "повторённое сложение". И чтобы расширить её свойства до "умножения" надо провести исследования этой операции. Поэтому крайне логично, что сначала вводят более простую и естественную операцию, а потом более сложную и общую.
ребенок выполняет множество формальных правил, за которыми стоит СМЫСЛ.еще больше выполняется соглашений.
например, все следующие записи эквивалентны
2 * 9
9 * 2
2*9
2* 9
9 *2
9 * 2
два * 9
2
*
9
9*
2
2 умножить на 9
перемножить 2 и 9
умножить 2 на девять
но при этом есть неявное соглашение, что в читабельном математическом тексте допустимы только два варианта:
"2 * 9" или "9 * 2".
Эти соглашения используются для увеличения читабельности текста.
Добавление еще одного явного проговоренного соглашения (справедливого при записи решений определенных задач) к десятку имеющихся неявных соглашений - погоды не делает, но чуть-чуть улучшает читабельность решения.
Добавление еще одного явного проговоренного соглашения к десятку имеющихся неявных соглашений - погоды не делает, но чуть-чуть улучшает читабельность решения.улучшает читабельность? то есть 2*9 как-то "лучше читается", чем 9*2?
ладно, я пас, это бред, и больше всего удивляет, что в этом бреде принимают участие выпускники МГУ. Белошистая победила.
улучшает читабельность? то есть 2*9 как-то "лучше", чем 9*2?да, улучшает читабельность при решении заданного класса задач начальной школы.
ps
2 * 9 лучше записи 9 * 2 тем, что этого придерживаются и остальные ученики в классе.
Это аналогичному тому, что "корова" лучше, чем "карова" только тем, что такой записи придерживаются и остальные,
ходить по правой стороне дороги лучше (чем по левой) тем, что этого придерживаются и остальные,
испльзовать метры(единицы Си) для измерения лучше тем, что это используют и остальные,
использовать для обозначения неизвестного буквы x, а не какого-то другого символа лучше тем, что так делают и остальные
использовать для обозначения сторон маленькие буквы, а углов - большие буквы лучше тем, что так делают и остальные
и т.д.
2 * 9 лучше записи 9 * 2 тем, что этого придерживаются и остальные ученики в классе.О, как! А миллионы мух не могут ошибаться, да.
ходить по правой стороне дороги лучше (чем по левой) тем, что этого придерживаются и остальные,Если ты используешь вместо метров аршины, тебя неправильно поймут, если ты напишешь 9*2 вместо 2*9, ничего страшного не случится.
испльзовать метры(единицы Си) для измерения лучше тем, что это используют и остальные,
использовать для обозначения неизвестного буквы x, а не какого-то другого символа лучше тем, что так делают и остальные
2 * 9 лучше записи 9 * 2 тем, что этого придерживаются и остальные ученики в классе.вот с каровой ты правильно сравнил. Введение принципа 2*9 =/= 9*2 - это всё равно, что заставлять на диктанте писать слово "карова" и снижать оценку за написание "корова". Конечно, весь класс будет писать одинаково, одинаково неправильно.
Имхо, до тех пор, пока дети не могут усвоить коммутативный закон нужно просто вводить непересекающуюся с традиционной систему символов. Чтобы за ради упрощения не жертвовать истиной. А то получится как в книжках "компьютер для блондинок" - куча вредной и неправильной информации.
Ну это уже вообще ЛОЛ. Ага, давайте детей (всех скопом) заранее готовить, что есть и некоммутативное умножение.
Ну, по моим воспоминаниям вдалбливалась именно коммутативность, а не некоммутативность. Она в общем-то и неочевидна. Вот повторяли же всё время: "От перемены мест сомножителей произведение не меняется", так же примерно как "жи ши пиши с буквой и".
Так что коммутативность для ребёнка не по умолчанию существует, а надо рассказать.
О, как! А миллионы мух не могут ошибаться, да.передергиваешь.
Речь идет о том, что есть варианты, которые при абстрагировании от уже сделанных выборов людей - одинаковые по лучшести.
И для таких ситуаций для удобства:
1. один из вариантов искусственно принимается как более лучший
2. выдается рекомендация или устанавливается правило, что именно этот вариант должен использоваться.
3. если использование уже вовсю идет, то в п.1 выбирается тот вариант, который использует большинство.
Имхо, до тех пор, пока дети не могут усвоить коммутативный закон нужно просто вводить непересекающуюся с традиционной систему символов.тебя бы в министры образования. чтоб добить уже просто.
Ну у тебя аргумент только один: что когда ты учился, тебя учили так. А всё что отличается — бред (ты понять не в состоянии)
2. выдается рекомендация или устанавливается правило, что именно этот вариант должен использоваться.мне кажется тебе не стоит останавливаться на реформе математического образования, предлагаю тебе приложить все силы к тому, чтобы запретить синонимы в курсе русского языка.
Если ты используешь вместо метров аршины, тебя неправильно поймут, если ты напишешь 9*2 вместо 2*9, ничего страшного не случитсядля меня ничего страшного не случится, если это и записать как: * 2 9. Но это только потому, что я уже знаком с префиксной записью выражений.
или другими словами, ничего страшного не случается, только если пишущий и читающий уже знакомы с коммутативным законом умножения и правильно его используют
но если речь идет про начальную школу, то эти обе презумпции и не выполняются.
ps
в данном случае, совершается стандартная ошибка недооценки значимости наличия неосознанного знания. Ты имеешь неосознанное знание, что 9 * 2 и 2 * 9 всегда эквивалентны, и неосознанно проецируешь это на других: что все остальные субъекты безусловно имеют такое же знание.
Пожалуй пошлю белошистой ссылку на этот тред. МГУ одобряет.
или другими словами, ничего страшного не случается, только если пишущий и читающий уже знакомы с коммутативным законом умножения и правильно его используютВот почему коммутативность надо вводить одновременно с умножением.
но если речь идет про начальную школу, то эти обе презумпции и не выполняются.
Вот почему коммутативность надо вводить одновременно с умножением.ну и изоморфность до кучи
мне кажется тебе не стоит останавливаться на реформе математического образования, предлагаю тебе приложить все силы к тому, чтобы запретить синонимы в курсе русского языка.во-первых, сторого говоря в русском языке нет синонимов, т.к. у каждого слова свои смысловые нюансы.
во-вторых, ты хочешь сделать еще более нереализуемую крайность - убрать из русского языка все омонимы. (Предлагаю начать со знака "-". Сделать различные символы для обозначения бинарной операции минус, унарного минуса и дефиса.)
вообще, мне не очень понятно, почему все согласны с соглашением kx (сначала пишется числовой коэффициент, а лишь потом значение
но несогласны с этим же соглашением, когда и k, и х выражены числами.
но несогласны с этим же соглашением, когда и k, и х выражены числами.
понимаешь, все согласны, что так удобнее, но никто не будет обвинять соседа в неправильном решении, если он переставит их местами. Иногда, кстати, удобнее и переставить. Вот, например, в случае ортогональной матрицы вообще любят переставлять местами вектор и матрицу коэфициентов, чтобы не рисовать обратной матрицы.
Ты говоришь, что нет смысла вводить коммутативность на таком раннем этапе, возможно ты прав. Но точно так же нет смысла и настаивать на единственной каноничной записи. Более того есть вред. Ложноположительные срабатывания, когда учитель считает, что ученик уже осознал коммутативность, а тот этого не сделал, куда лучше, чем ложноотрицательные, когда ученик уже всё понял, а учитель настаивает, что тот дурак. Потому что в последнем случае у ребёнка разовьётся ненависть к учёбе. Он бросит математику в третьем классе, а потом научное общество будет удивляться, почему уличное общество на опросах демонстрирует такой катастрофический уровень безграмотности.
Но и ложноположительные срабатывания тоже плохи, хотя и не так плохи, как ложноотрицательные. Поэтому я и предлагаю ввести расширенные обозначения, дабы избежать двусмысленностей
Ты говоришь, что нет смысла вводить коммутативность на таком раннем этапе, возможно ты прав. Но точно так же нет смысла и настаивать на единственной каноничной записи. Более того есть вред. Ложноположительные срабатывания, когда учитель считает, что ученик уже осознал коммутативность, а тот этого не сделал, куда лучше, чем ложноотрицательные, когда ученик уже всё понял, а учитель настаивает, что тот дурак. Потому что в последнем случае у ребёнка разовьётся ненависть к учёбе. Он бросит математику в третьем классе, а потом научное общество будет удивляться, почему уличное общество на опросах демонстрирует такой катастрофический уровень безграмотности.
Но и ложноположительные срабатывания тоже плохи, хотя и не так плохи, как ложноотрицательные. Поэтому я и предлагаю ввести расширенные обозначения, дабы избежать двусмысленностей
во-первых, сторого говоря в русском языке нет синонимов, т.к. у каждого слова свои смысловые нюансы.можно расписать таблицу применимости. В какой области какое слово допустимо к использованию
Вот почему коммутативность надо вводить одновременно с умножением.это запутает тех, кто может в единицу времени усваивать лишь небольшое кол-во нового.
Есть два различных навыка:
1. перевести словесное описание задачи в математическое описание
2. выполнить над мат. описанием ряд эквивалентных преобразований
при этом строго сначала должно делаться первое, и только потом второе. При постановке умения - это желательно иллюстрировать на бумаге, а потом, конечно, можно делать и в уме.
Если же эти два навыка не разделены, то начинается бардак и интуитивные догадки, что и видно на примере: Решающие что-то делают, но не могут объяснить ни что они делают, ни как это соотносится с исходной постановкой задачи.
И строго говоря, эквивалентность записей 2 * 9 и 9 * 2 появляется лишь на втором этапе, на первом этапе они не эквиваленты.
Но точно так же нет смысла и настаивать на единственной каноничной записи.я считаю, что правильнее разделять оценки: за смысл и за оформление. И вообще, чем больше разных оценок, тем лучше - это ускоряет процесс обучения, если, конечно, при этом не происходит подмены оценки правильности на развешивание ярлыков хороший/плохой.
Соответственно, замена 2 * 9 на 9 * 2 - это уменьшение оценки за оформление, но оценка за смысл остается той же самой.
Поэтому я и предлагаю ввести расширенные обозначения, дабы избежать двусмысленностейЭто, конечно, с методической точки зрения ничего хорошего не даст, вспомни что не о студентах-первокурах речь, а о 7-летних детях
[
Более того, даже в картинке из интернета непонятно, за что именно стоит тройка, может там выше ещё дохрена ошибок или неправильных решений было. Или ещё чего.
Соответственно, замена 2 * 9 на 9 * 2 - это уменьшение оценки за оформление, но оценка за смысл остается той же самой.Что-то вы всё в кучу мешаете. В этом треде вообще речь вообще не о той картинке, где 2*9 и 9*2, а цитаты из методички Белошистой. Там вообще речь не идёт о том, как за это оценки ставить и так далее.
Более того, даже в картинке из интернета непонятно, за что именно стоит тройка, может там выше ещё дохрена ошибок или неправильных решений было. Или ещё чего.
Ложноположительные срабатывания, когда учитель считает, что ученик уже осознал коммутативность, а тот этого не сделал, куда лучше, чем ложноотрицательные, когда ученик уже всё понял, а учитель настаивает, что тот дурак.Да, конечно, это плохо. Но причём тут настаивание учителя что ученик дурак? И какое это отношение имеет к обсуждаемой педагогической методике?
Потому что в последнем случае у ребёнка разовьётся ненависть к учёбе. Он бросит математику в третьем классе,Ну, а это вообще фантазии от мегасоциолога и детского психолого аувангоу
Соответственно, замена 2 * 9 на 9 * 2 - это уменьшение оценки за оформление, но оценка за смысл остается той же самой.и ребёнок навсегда запомнит, что умножение некоммутативно. А потом будет жаловаться, что его в школе обманули. Хочешь вводить однотипную запись - введи новый символьный инструментарий, который не пересекается с обычным умножением. Иначе это инструмент отпугивания от математики одарённых детей (и упрощение для неодарённых)
Да, конечно, это плохо. Но причём тут настаивание учителя что ученик дурак? И какое это отношение имеет к обсуждаемой педагогической методике?я отвечал па полст даркгрея, где он говорил, что правильная запись позволяет учителю проверить, что ученик правильно усвоил урок
Ну, а это вообще фантазии от мегасоциолога и детского психолого аувангоуну я плохой социлог, но один знакомый, бросивший в школе математику (её, кстати, по методичке читала учитель пения) в районе пятого класса у меня есть. Точно так же из собственного опыта я знаю, как преподаватель истории может привить устойчивую ненависть к своему предмету.
и ребёнок навсегда запомнит, что умножение некоммутативно.При правильной методологии ребенок усвоит, что сначала надо аккуратно переписать текст в мат. описание, а только потом применять эквивалентные преобразования. И это ему позволит легко решать сложные задачи, где ранние эквивалентные преобразования лишь всё еще больше запутывают.
например, в следующей задаче:
В коробке 5 конфет. Маша взяла 1 коробку. Сколько конфет у маши?
Можно ведь тоже сразу написать: 5.
Но с точки зрения усвоения навыка аккуратной переформулировки задачи в виде мат. описания, то правильнее сначала записать:
1 * 5
и только потом применять правила сокращения или численного вычисления.
А потом в качестве триумфа математической науки ввести *, доказав ассоциативность операцииТы, видимо, имел в виду коммутативность. Впрочем и ассоциативность и коммутативность умножения являются аксиомами в одной из формализация арифметики Пеано. Поэтому что ты доказывать детям собрался я не понимаю. Если эквивалентность разных формализаций арифметики, то ты совсем ебанулся.
В коробке 5 конфет. Маша взяла 1 коробку. Сколько конфет у маши?
Но с точки зрения усвоения навыка аккуратной переформулировки задачи в виде мат. описания, то правильнее сначала записать:но ведь по твоей логике следует писать 5 * 1!
1 * 5
Ты, видимо, имел в виду коммутативность. Впрочем и ассоциативность и коммутативность умножения являются аксиомами в одной из формализация арифметики Пеано.вики об арифметики Пеано
Ну и где коммутативность, ассоциативность и прочее? Всё нужно доказывать по индукции.
- 1 является натуральным числом;
- Число, следующее за натуральным, тоже является натуральным;
- 1 не следует ни за каким натуральным числом;
- Если натуральное число a непосредственно следует как за числом b, так и за числом c, то b и c тождественны;
- (Аксиома индукции.) Если какое-либо предложение доказано для 1 (база индукции) и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за n натурального числа (индукционное предположение то это предложение верно для всех натуральных чисел.
Формализация арифметики включает в себя аксиомы Пеано, а также вводит число 0 и операции сложения и умножения с помощью следующих аксиом:
- x+0=x;
- x_1+S(x_2)=S(x_1+x_2);
- x * 0=0;
- x_1 * S(x_2)=x_1 * x_2+x_1.
но ведь по твоей логике следует писать 5 * 1!в данном случае я использовал соглашение: разы * штуки (это может не совпадать с тем соглашением, что требовалось в цитируемом учебнике)
т.к. нужно получить кол-во конфет, а не коробок, то коробки - это разы, а конфеты - это штуки. 1 идет на первое место, а 5 на второе.
Но с точки зрения усвоения навыка аккуратной переформулировки задачи в виде мат. описания, то правильнее сначала записать:Но никто не должен мешать писать в ответе число 5, если в разделе решения указано 5*1 = 1*5 = 5. Матчить правильность решения только по ответу - это блажь и глупость
1 * 5
Но никто не должен мешать писать в ответе число 5правильность этого утверждения зависит от постановки задачи.
Если задача звучит как:
переведите текстовое описание в корректное мат. описание,
то правильный ответ:
1 * 5, а не 5.
переведите текстовое описание в корректное мат. описание,корректное может быть и 5*1
А ещё лучше, чтобы такой задачи вообще не ставилось никогда, потому что она учит отрываться от реальности и осмысленности.
А излишний формализм приводит к тому, что ООП заставляют учить, переводя все функции в методы одного статического класса.
в данном случае я использовал соглашение: разы * штуки (это может не совпадать с тем соглашением, что требовалось в цитируемом учебнике)то есть задачу из первого поста ты тоже неправильно решил?
вики об арифметики Пеаноwiki об арифметике Пеано
Если ты не заметил, я написал, что коммутативность и ассоциативность умножения это аксиомы некоторых формализаций. Еще раз, если ты собираешься детям в начальной школе доказывать, что эти формализации эквивалентны, то ты ебанулся.
то есть задачу из первого поста ты тоже неправильно решил?Решил правильно, оформил не правильно.
вообще в школе проходят мат индукцию. Так что и вывести свойства операций над натуральными числами не только можно, но и нужно. Впрочем, любопытные могут это сделать самостоятельно, но не надо при этом гнобить любопытных.
Ты предлагаешь умножение изучать в ~9-ом классе, когда сейчас изучают индукцию? Или индукцию во ~2-ом классе, когда сейчас изучают умножение? Или может быть все-таки постулировать коммутативность умножения во ~2-ом классе (тем более это аксиома в некоторых формализациях арифметики)?
Ты предлагаешь умножение изучать в ~9-ом классе, когда сейчас изучают индукцию? Или индукцию во ~2-ом классе, когда сейчас изучают умножение? Или может быть все-таки постулировать коммутативность умножения во ~2-ом классе (тем более это аксиома в некоторых формализациях арифметики)?я предлагаю в первом классе изучить кастомный сет операций. Между первым и вторым выучить таблицу умножения в стиле "это просто магия,
ладно, я пас, это бред, и больше всего удивляет, что в этом бреде принимают участие выпускники МГУ. Белошистая победила.+1
причём ладно, если быть речь шла о каких-то сложных алгебраических преобразованиях. Но тут, блин, когда всерьёз считают, что надо снижать оценку за офорление, если 2*5 "перепутано" с 5*2... Я просто не понимаю, куда я попал. России, видимо, суждено утопать в бюрократии, если даже здесь находятся защитники подобного бреда.
За всем стоит смысл. С сахаром он нагляден — можно легко представить себе 5 рядов по два кусочка сахара. А если на этот сахар посмотреть с другой стороны, то уже будет 2 ряда по 5 кусков. Наглядное представление умножения, из которого очевидна и коммутативность, и всё остальное. И понятно, что записи 2*5 и 5*2 равносильны.
Даже без такой интерпретации, 2*5 и 5*2 эквивалентны. Просто потому, что в русском языке эквивалентны предложения "в пяти чашках по два кусочка" и "по два кусочка в пяти чашках", нет никакой логики в приоритете какой-либо из форм записи.
PS: в общем, я завязываю со спорами. Это бесполезно. Но мысли тред грустные вызывает.
Наглядное представление умножения, из которого очевидна и коммутативность, и всё остальноегифка с вечным
я предлагаю в первом классе изучить кастомный сет операций.Это какой, левое и правое умножение? Заодно еще и левое/правое деление? Левые/правые рациональные числа?
сложение и повторное сложение
Левое или правое сложение?
коммутативность сложения можно постулировать аксиоматически
Но тут, блин, когда всерьёз считают, что надо снижать оценку за офорление, если 2*5 "перепутано" с 5*2...в старшей школе не надо, а в начальной желательно.
Так же как за чистописание - в старшей школе не снижают, а в начальной снижают.
Или за наличие слова "Ответ", или за правильность написания буквы т, или за попадание цифр в клеточки, или за совпадение слов и линеечек и т.д.
На каждом этапе школы формируется свой навык, и оценивание навыка улучшает его формирование.
коммутативность сложения можно постулировать аксиоматическиА почему нельзя постулировать аксиоматически коммутативность умножения?
в старшей школе не надо, а в начальной желательно.какое чистописание? Или даже какой стиль, какие соглашения? Соглашения, это писать 2*x^2, вместо x^2 * 2.
Так же как за чистописание - в старшей школе не снижают, а в начальной снижают.
Говоря, что лучше 2*5 вместо 5*2, ты тем самым ошибке учишь. Вместо того, чтобы мозг утвердился в том, что так правильно, ты предлагаешь пытаться учить какие-то нелепые правила, что нужно ставить сначала, а что потом, искать какую-то логику в этом. В итоге, чтобы не стоящий за решением смысл понимать, а запомнить формулы и не думая подставлять туда цифры из задачи.
PS: нет, честно, надеюсь тут не только стебётся, но и другие тоже.
на самом деле, имхо, многие форумчане не помнят, чему и в каком порядке их учили в началке. Они говорят: "это чушь, к счастью, нам все объясняли по-другому", но на самом деле это может лишь означать, что в том возрасте они спокойно относились к таким требованиям, а когда подросли, требования естественным образом изменились. Я это регулярно вижу на примере более старших детей, когда родители помогают им делать домашку: обладая более широкими и глубокими знаниями, родители просто не могут "опуститься" до уровня своих детей.
Я не знаю, на самом деле осмысленны конкретно эти методические рекомендации или нет, но знаю точно, что с мехматовским образованием рассуждать об обучении в началке довольно глупо. Для этого нужно сначала попробовать чему-нибудь научить ребенка, обращая внимание на 2 момента: 1) лично ваш ребенок скорее всего более быстро схватывает, чем его одноклассники, поэтому он не показателен; 2) нужно научить стабильно решать не одну задачу, а достаточно широкий класс, например, может оказаться, что задачки на умножение ребенок научится щелкать как орешки, а вот с делением впоследствии начнет нести прекрасную ахинею.
Обычно обучение устроено так: сначала вводятся довольно строгие формальные правила и от ребенка требуется постоянно объяснять свои действия, потом, когда ошибки в принципиальных моментах сойдут на нет, ограничения снимаются и детей, наоборот, учат применять всякие фишки для упрощения счета, и непременение этих фишек карается по крайней мере у сильных и средних детей.
что касается "сильно умных", имхо, если они в состоянии понять, что правило легко можно нарушать, значит, они в состоянии его и выполнить. Со стороны родителей проблему скуки полезно решать кружками, если это иногда, или спецшколой, если это постоянно.
Учителя стоит оценивать по некоторым рубежным работам, проверяя, что научился решать ребенок, а не по тому, что он где-то в домашке снижает оценку за оформление. Как оценивать методиста, хз, например, можно посоветоваться с хорошим учителем началки.
Я не знаю, на самом деле осмысленны конкретно эти методические рекомендации или нет, но знаю точно, что с мехматовским образованием рассуждать об обучении в началке довольно глупо. Для этого нужно сначала попробовать чему-нибудь научить ребенка, обращая внимание на 2 момента: 1) лично ваш ребенок скорее всего более быстро схватывает, чем его одноклассники, поэтому он не показателен; 2) нужно научить стабильно решать не одну задачу, а достаточно широкий класс, например, может оказаться, что задачки на умножение ребенок научится щелкать как орешки, а вот с делением впоследствии начнет нести прекрасную ахинею.
Обычно обучение устроено так: сначала вводятся довольно строгие формальные правила и от ребенка требуется постоянно объяснять свои действия, потом, когда ошибки в принципиальных моментах сойдут на нет, ограничения снимаются и детей, наоборот, учат применять всякие фишки для упрощения счета, и непременение этих фишек карается по крайней мере у сильных и средних детей.
что касается "сильно умных", имхо, если они в состоянии понять, что правило легко можно нарушать, значит, они в состоянии его и выполнить. Со стороны родителей проблему скуки полезно решать кружками, если это иногда, или спецшколой, если это постоянно.
Учителя стоит оценивать по некоторым рубежным работам, проверяя, что научился решать ребенок, а не по тому, что он где-то в домашке снижает оценку за оформление. Как оценивать методиста, хз, например, можно посоветоваться с хорошим учителем началки.
объясни, пожалуйста, без использования коммутативного закона и без использования тавтологичного правила "ответ неправильный получится" почему когда речь идет о задаче:
было 5 птиц, потом из них 3 улетело,
можно писать: 5 - 3, но нельзя писать 3 - 5
а для задачи:
было 5 птиц, потом к ним 3 прилетело,
можно писать: 3 + 5 и 5 + 3
Тоже самое и про умножить и разделить.
Объясни, пожалуйста, без использования коммутативного закона почему для задачи:
10 конфет разделили между 5 детьми поровну
можно писать: 10 / 5, но нельзя 5 / 10
а для задачи:
5 детям раздали по 2 конфеты
можно писать:
2 * 5 и 5 * 2
Вот такая зубрежка на ранних стадиях: это можно писать двумя способами, а это можно писать только одним способом - лишь еще больше всех запутывает и приводит к отсутствию понимания.
было 5 птиц, потом из них 3 улетело,
можно писать: 5 - 3, но нельзя писать 3 - 5
а для задачи:
было 5 птиц, потом к ним 3 прилетело,
можно писать: 3 + 5 и 5 + 3
Тоже самое и про умножить и разделить.
Объясни, пожалуйста, без использования коммутативного закона почему для задачи:
10 конфет разделили между 5 детьми поровну
можно писать: 10 / 5, но нельзя 5 / 10
а для задачи:
5 детям раздали по 2 конфеты
можно писать:
2 * 5 и 5 * 2
Вот такая зубрежка на ранних стадиях: это можно писать двумя способами, а это можно писать только одним способом - лишь еще больше всех запутывает и приводит к отсутствию понимания.
Объясни, пожалуйста, без использования коммутативного закона почему для задачи:Почему нельзя? Можно! 10/5 конфет на ребенка эквивалентно 5/10 ребенка на конфету.
10 конфет разделили между 5 детьми поровну
можно писать: 10 / 5, но нельзя 5 / 10
на самом деле, имхо, многие форумчане не помнят, чему и в каком порядке их учили в началке. Они говорят: "это чушь, к счастью, нам все объясняли по-другому", но на самом деле это может лишь означать, что в том возрасте они спокойно относились к таким требованиям,нет, неправда.
У меня в классе было 2 мальчика (я и ещё один которым всё было просто очевидно по математике, всё в момент схватывали и писали как хотели. Меня, например, не могли заставить в столбик делить (на редкость тупое заняние хотя умножал и складывал я, всё же, скорее в столбик. О каких-то из училок, что в начальной школе были, было мнение (обоснованное даже что они тупые.
Хотя у многих математика вызывала большие проблемы, дети просто не понимали очевидных, казалось бы, вещей. Могу полагать, что как раз потому, что всё очень буквально воспринимали, как учителя рассказывали. А ведь программа математики в начальной школе такая, что как только поймёшь смысл, всё сразу становится очевидным просто.
Это бесполезно. Но мысли тред грустные вызываетага, как будто в дурдом попал, и типа надо объяснять пациентам типа гимли что-то. а если ты не понял их "правоту" - ну все, узколобый. Честно говоря, этот тред шокирует почище методички.
Пиздец, оказывается в русском языке нет синонимов еще, я узнал.
На каждом этапе школы формируется свой навык, и оценивание навыка улучшает его формирование.Эээ, а сделай-ка голосовалку относительно того, насколько снижение оценок в прописях за ровность буковок улучшило навык чистописания у форумчан? Лично меня это всегда НАСТОЛЬКО бесило, что не передать словами. Я отлично в первом классе понимала, за что мне снижают оценку. И я точно так же отлично понимала, НАСКОЛЬКО это бредово по сути того, что происходит в школе. И троллила одноклассниц с идеальным почерком, но которые хуже меня считали или делали ошибки орфографические в словах. В итогев классе было 2 человека, которые испытывали проблемы с логической связкой "хуже оценка - лучше писать будет" -
а) я, которая бесилась от этого неимоверно (почерк, кстати, так и не улучшился
)и па-ба-бам!
б) классный руководитель, она же учитель русского языка и математики. Так как ей совесть не позволяла ставить самой соображающей ученице класса плохие оценки, но требования методики и её собственноручно выставленные оценки не оставляли ей выбора. В итоге в конце каждой четверти в 1 классе мы наблюдали комедию с приходом моей мамы в школу и попыткой учительницы повоздействовать на меня через неё со словами "Я понимаю, что ваша дочь - лучшая ученица, она помогает другим ученикам и т.д., но я не могу поставить ей выше тройки - у неё столько двоек за чистописание. А 3 мне совесть поставить не позволяет, да и не знаю, как буду смотреть в глаза другим ученикам, так как ваша дочь объективно лучше них владеет материалом, много и бегло читает, знает таблицу умножения"
Я к тому, что формальное оценивание оформления на самом деле не выход, так как это подрывает интуитивное понимание того, что обучение и мыслительная работа - это огромная самоценнсть, у всех детей.насколько снижение оценок в прописях за ровность буковок улучшило навык чистописания у форумчанне оценка должна снижаться, а должна быть вторая оценка за аккуратность.
Тогда во-первых есть за что хвалить аккуратных "тугодумов", а во-вторых, есть что подтягивать неаккуратным "смысленышам"
У нас, если что, так и было. Но это не помогало Хинт - лучше всего лично мне помог чит другой учительницы, которая временно заменяла нашу - она просто отказывалась понимать совсем уж плохо написанные строки и снижала оценку за якобы ошибки (не трогая чистописание). Я, естественно, бросалась в бой, доказывая, что там нет ошибок. Она делала удивлённые глаза - надо же, а я не поняла. Давай тогда выполни ещё пару упражнений, но теперь постарайся написать так, чтобы я с первого раза поняла, что там написано, чтобы не пришлось нам обеим сидеть и разбирать это. Кстати, она не снижала оценку за свои же исправления ошибок, так как считала, что это хорошо, когда ребёнок сам увидел ошибку и исправил её. В общем, она единственная, которая юзала чистописание для того же, для чего и нужно - чтобы письмо школьника было правильно понято другими, а не как самоценность.
Хинт - лучше всего лично мне помог чит другой учительницы, которая временно заменяла нашу - она просто отказывалась понимать совсем уж плохо написанные строки и снижала оценку за якобы ошибки (не трогая чистописание). Я, естественно, бросалась в бой, доказывая, что там нет ошибок. Она делала удивлённые глаза - надо же, а я не поняла. Давай тогда выполни ещё пару упражнений, но теперь постарайся написать так, чтобы я с первого раза поняла, что там написано, чтобы не пришлось нам обеим сидеть и разбирать это. Кстати, она не снижала оценку за свои же исправления ошибок, так как считала, что это хорошо, когда ребёнок сам увидел ошибку и исправил её. В общем, она единственная, которая юзала чистописание для того же, для чего и нужно - чтобы письмо школьника было правильно понято другими, а не как самоценность.было 5 птиц, потом из них 3 улетело,а не надо учить записи и потом формально с ними оперировать, надо смысл понимать! Потому что написать 3 - 5 можно, только не понимая, что эта запись вообще означает. То есть, если дитё написало 3-5, то это сигнал, что тут провал в понимании, и над этим надо работать.
можно писать: 5 - 3, но нельзя писать 3 - 5
ну примерно как не надо учить детей, что предложения "собака укусила кошку" и "кошку укусила собака" эквавалентны. А вот "моль ест шерсть" и "шерсть ест моль" уже не совсем эквивалентны, хотя казалось бы... Просто для владеющего русским языком это очевидно, и лингвистику для этого изучать не обязательно.
про коммутативность уже нужно вспоминать, когда идёт работа с формальными вычислениями.
все не в ногу, один я в ногу? Хватит уже чесать свое чсв. Нет, ты не единственный всё понявший МГУшник, ты просто действительно узколобый.
Вообще мне вот интересно, что вспоминая школу все приводят примеры из разряда "как глупая училка нелепо притесняла умного меня". А обратных примеров у вас совсем нет?
Я например из университетстких времен такой храню. Я тогда нашу семинаристку по механике кляла неделю где-то разными словами, за то что она настаивала на какой-то одной формулировке определения, а эквивалентную не принимала. И я ходила всю неделю и думала: "Мы не гуманитарии, мы 4 курс мехмата! Какое нам дело до выбора слов, если суть одна! Как она смела вообще с такими претензиям к нам! Да как её допустили здесь преподавать!..." и всё в таком духе, очень много ругалась
А потом ещё через неделю я вдруг поняла разницу в тех двух определениях, из-за которых был спор. Да, она конечно была ужасная семинаристка, и сдается мне сама ту разницу так и не поняла или по крайней мере не смогла бы объяснить. Но я-то её увидела. И мне было очень стыдно
Вообще мне вот интересно, что вспоминая школу все приводят примеры из разряда "как глупая училка нелепо притесняла умного меня". А обратных примеров у вас совсем нет?
Я например из университетстких времен такой храню. Я тогда нашу семинаристку по механике кляла неделю где-то разными словами, за то что она настаивала на какой-то одной формулировке определения, а эквивалентную не принимала. И я ходила всю неделю и думала: "Мы не гуманитарии, мы 4 курс мехмата! Какое нам дело до выбора слов, если суть одна! Как она смела вообще с такими претензиям к нам! Да как её допустили здесь преподавать!..." и всё в таком духе, очень много ругалась
А потом ещё через неделю я вдруг поняла разницу в тех двух определениях, из-за которых был спор. Да, она конечно была ужасная семинаристка, и сдается мне сама ту разницу так и не поняла или по крайней мере не смогла бы объяснить. Но я-то её увидела. И мне было очень стыдно
ты просто действительно узколобыйзато тут несколько вас, "альтернативно одаренных".
А потом ещё через неделю я вдруг поняла разницу в тех двух определениях, из-за которых был спор.
ма-ла-дец. только на самом деле НЕТ разницы 2*9 или 9*2. а в чем ты там раньше разницу не понимала - боюсь было посложнее.
А почему нельзя постулировать аксиоматически коммутативность умножения?потому что умножение менее очевидное действие. Тут уже высказывались сомнения в том, что одноклассник способен одновременно с введением умножения как последовательности сложения ещё и осознать принцип коммутативности. Поэтому я считаю целесообразным отложить этот момент до выучивания таблицы умножения
правильная запись позволяет учителю проверить, что ученик правильно усвоил урокЧто не имеет никакого отношения к настаиванию что ученик дурак
Поэтому я считаю целесообразным отложить этот момент до выучивания таблицы умноженияТо есть ты поменял свое предыдущее мнение:
А потом в качестве триумфа математической науки ввести *, доказав ассоциативность операции.
Или ты предлагаешь одновременно с выучиванием таблицы умножения доказывать коммутативность умножения использую какую-нибудь формализацию аксиоматики Пеано, которая коммутативность не объявляет аксиомой?
> только на самом деле НЕТ разницы 2*9 или 9*2
Во-первых, "разница" зависит от того как её мерить. Во-вторых, и в общепринятом смысле на самом-то деле разница есть, а вот результат после вычисления - да, одинаковый.
Но в твоем случае проблема не в этом конкретном примере, а в том, что ты до сих пор споришь именно про картинку из заглавного поста и не потрудился понять ни слова из того, что писали в этом треде.
Во-первых, "разница" зависит от того как её мерить. Во-вторых, и в общепринятом смысле на самом-то деле разница есть, а вот результат после вычисления - да, одинаковый.
Но в твоем случае проблема не в этом конкретном примере, а в том, что ты до сих пор споришь именно про картинку из заглавного поста и не потрудился понять ни слова из того, что писали в этом треде.
только на самом деле НЕТ разницы 2*9 или 9*2В этом треде обсуждают не то, есть ли разница между 2*9 и 9*2.
Или ты предлагаешь одновременно с выучиванием таблицы умножения доказывать коммутативность умножения использую какую-нибудь формализацию аксиоматики Пеано, которая коммутативность не объявляет аксиомой?Что здесь не понятного?
я предлагаю в первом классе изучить кастомный сет операций. Между первым и вторым выучить таблицу умножения в стиле "это просто магия, математическая магия". Тогда же и вплоть до пятого класса давать прочие приёмы устного счёта. В районе шестого класса, когда начинают проходить доказательную геометрию и геометрическую аксиоматику имени товарища Евклида, ввести аксиоматику арифметики.Я предлагаю объявить коммутативность магией. Заодно с ней научить признакам делимости, быстрому умножению на 11 и т.д. и т.п. И потом превратить магию в технологию. И уже самостоятельно предложить вычислить признаки делимости на большИе простые числа, скажем на 13 и 17.
Вводить аксиоматику стоит не раньше, чем ученики узнают, что такое аксиома и теорема. То есть в районе 6 класса, когда они это и так узнают из геометрии
что ты до сих пор споришь именно про картинку из заглавного постаДаже не из заглавного, этой картинки вообще в треде не было
Вообще мне до сих пор удивительно сколько срача вызвал этот вопрос, каким-то образом видимо задевает за живое. Я вот запостил два абзаца, так увидели оттуда только предолжение про то что "по таким учебникам учившиеся люди построили СССР ракету"
Я предлагаю объявить коммутативность магией. Заодно с ней научить признакам делимости, быстрому умножению на 11 и т.д. и т.п.Ну вроде в школе так и делают примерно.
А магией можно и запретить пользоваться на начальном этапе, это ж магия! Ну или хотя бы как тут: сначала напиши как положено, а потом уже магию применяй.
Ну вроде в школе так и делают.ну я по себе и судил. Но до того момента, когда эта магия будет объявлена, не использовать значок умножения. Дабы не искушать.
Но до того момента, когда эта магия будет объявлена, не использовать значок умножения.Лишние значки детям (особенно какие ты предлагал) — это точно зря
Ты сам написал, что:
Тем не менее теперь ты предлагаешь учить таблицу умножения (коммутативную!) во втором классе, а доказывать коммутативность умножения (что само по себе бред) в шестом.
Более того, пока не доказана коммутативность умножения для натуральных чисел, рановато вводить коммутативное умножение.
Тем не менее теперь ты предлагаешь учить таблицу умножения (коммутативную!) во втором классе, а доказывать коммутативность умножения (что само по себе бред) в шестом.
Да ладно удивляться-то. Тут же совмещены - ностальгическое "раньше небо было синее", личное "а вот я как-то раз на уроке как выдам..", политическое "против системы" и даже математические "градуированная алгебра оно или коммутативная группа".
типичная вирусная тема же, к которой просто невозможно не присоединиться )
типичная вирусная тема же, к которой просто невозможно не присоединиться )
Даже ты не удержалась!
Потому что написать 3 - 5 можно, только не понимая, что эта запись вообще означает. То есть, если дитё написало 3-5, то это сигнал, что тут провал в понимании, и над этим надо работать.Я просил объяснение: почему это неправильно?
Ответ неправильно, потому что неправильно - таким объяснением не является.
Ответ на вопрос "Почему неправильно" должен начинаться со слов: потому что нарушается следующее правило..
ps
Ты используешь шаманский подход к пониманию: надо сделать вот такой ритуал - сказать ученику, что это правильно, это тоже правильно, а вот это неправильно. И в ученике само собой появятся знания и алгоритмы по использованию этого знания, а если не появились, то значит ученик - тупой, и не способен это выучить.
Слушай, хочу спросить, я действительно непонятно формулировал свои мысли?
Я вот чо не понимаю до конца: а нафига детям чашки и птички во втором классе? В том плане, что заострять на них внимание, как на размерности некоторой неявно введеной в условии задачи системы единиц.
Я понимаю в дошкольном возрасте: два зайца плюс три зайца - типа пять зайчиков.
Во втором же классе можно еще давать такие образы, связанные с реальной жизнью, но не ебать же за порядок чисел в записи. А нормальные размерности класса с пятого пойдут, а не неведомая система ЧС (чашки/сахар).
Я понимаю в дошкольном возрасте: два зайца плюс три зайца - типа пять зайчиков.
Во втором же классе можно еще давать такие образы, связанные с реальной жизнью, но не ебать же за порядок чисел в записи. А нормальные размерности класса с пятого пойдут, а не неведомая система ЧС (чашки/сахар).
Я вроде понял
при звуках флейты теряю волю
Кстати, по опыту занятий с сыном могу сообщить следующее.
Дети неплохо воспринимают сложение и быстро его осваивают в том числе и на абстрактном уровне, то есть не два яблока плюс два яблока, а просто два плюс два. Однако, им уже не совсем очевидно множественное сложение 2+2+2+2+2. Но это преодолевается быстро. Далее надо ввести новую операцию - умножение. Так вот как это делается? Я не помню, в связи со старостью. Но из общих соображений умножение можно вводить как сокращенную запись множественного сложения. И тогда имеет смысл задать порядок множителей в произведении, чтобы отличать 3+3+3+3+3 от 5+5+5. Какой должен быть порядок в каком случае на самом деле не важно, но желательно его постулировать одинаковым для всех, чтобы при смене учителя, например, не произошло непонимание. Это исключительно методический нюанс, который позволяет получить уверенность, что ребенок правильно строит решение задачи, а не тупо подставляет числа в произведение для получения ответа по аналогии с другими решенными в классе задачами. Еще раз подчеркну, что речь идет о детях, которые только начинают изучать умножение. Причем изучать не на примерах, а на задачах. В дальнейшем решая обычные примеры на запоминание таблицы умножения будет видно, что множители можно переставлять.
Тем не менее, это не отменяет того факта, что методичке из первого поста написана чушь.
Дети неплохо воспринимают сложение и быстро его осваивают в том числе и на абстрактном уровне, то есть не два яблока плюс два яблока, а просто два плюс два. Однако, им уже не совсем очевидно множественное сложение 2+2+2+2+2. Но это преодолевается быстро. Далее надо ввести новую операцию - умножение. Так вот как это делается? Я не помню, в связи со старостью. Но из общих соображений умножение можно вводить как сокращенную запись множественного сложения. И тогда имеет смысл задать порядок множителей в произведении, чтобы отличать 3+3+3+3+3 от 5+5+5. Какой должен быть порядок в каком случае на самом деле не важно, но желательно его постулировать одинаковым для всех, чтобы при смене учителя, например, не произошло непонимание. Это исключительно методический нюанс, который позволяет получить уверенность, что ребенок правильно строит решение задачи, а не тупо подставляет числа в произведение для получения ответа по аналогии с другими решенными в классе задачами. Еще раз подчеркну, что речь идет о детях, которые только начинают изучать умножение. Причем изучать не на примерах, а на задачах. В дальнейшем решая обычные примеры на запоминание таблицы умножения будет видно, что множители можно переставлять.
Тем не менее, это не отменяет того факта, что методичке из первого поста написана чушь.
Я просил объяснение: почему это неправильно?выражение "5-3" интерпретируется примерно так:
Ответ неправильно, потому что неправильно - таким объяснением не является.
line = "5 - 3"
if re.match(r"\d+\s*-\s*\d+", line):
we_are_reading = "от " + line.replace("-", ' отнтять ')
else:
we_are_reading = "что это (%s)?" % line
print (we_are_reading)
оно просто читается как "от пяти отнять три", и проблем вызывать не должна. Тут никакой магии нет, никаких математических свойств запоминать не надо, просто надо уметь читать. Человек читает это выражение по-русски, и сразу в голове образ возникает, как от пяти птичек отнимается три. Я не понимаю, а как иначе ещё?
это даже не правило, как "жи-ши". Это банальное умение читать цифры и значки. В первом классе этому уже учатся.
оно просто читается как "от пяти отнять три",в исходной постановке не было слов "от .. отнять .."
Ты нормально сформулировал, просто не тому: Вован тут умнее всех, ведь четвертый результат на мосгоре почти двадцать лет назад, и он не читает твои посты, а несет тебе Истину.
Но я-то её увидела. И мне было очень стыдноВообще- то ту никто не утверждал, что в ЛЮБОМ требовании что-то сделать вот так, а не иначе, нет внятных логических оснований. Однако большинство считает, что в обсуждаемом вопросе последовательность множителей есть всего лишь результат договорённостей по другим, нежели логическое обоснование, причинам. И по сути, как я понимаю, речь идёт о
а) необходимости безусловного применения этих договорённостей ко всем ученикам
б) необходимости оценивания невыполнения этих договорённостей.
в) обоснованность такой договорённости в конкретном случае сомножителей.
ем не менее, это не отменяет того факта, что методичке из первого поста написана чушь.Там написано то же самое, что говоришь ты, только она не смогла это нормально сформулировать
Причем изучать не на примерах, а на задачах.Вот здесь, у меня ощущение, и есть причина расхождений во мнениях. Я вспоминаю проблемы у племянницы, которая не могла тоже поймать суть какой-то операции. И не могла именно из-за задач. Свекровь обучала её на примерах БЕЗ необходимости какого-либо внятного оформления и без предметного приложения, а только на абстрактных числах, так как уж числа она знала точно, и сложение знала точно. И за вечер на 15-20 примерах девочка обучилась и поняла суть. Если бы она продолжала обучаться на задачах, в которых одно оформление занимает львиную часть времени, а само решение - секунды, то она по-прежнему бы пыталась что-то расположить и оформить, а не уловила бы суть. И тогда возможно, и приходилось бы настаивать на определённом порядке сомножителей.
Т.е. лично я не уверена, что задачный принцип обучения умножению с необходимостью такого упорядоченного оформления методически глобально оправдан. Возможно я не права, но мне кажется более полезным обучать принципу умножения как сложения на кубиках рядами и столбиками, сразу понять про перестановку множителей, освоить простое умножение на примерах. И только потом искать умножение в реальной жизни, т.е. искать задачи и решать их уже освоенной операцией + учиться находить её там.
И относительно преемственности необходимости оформления в младшей школе и оформления задач по физике в средней и старшей. Моё глубокое убеждение - нет там никакой преемственности. Есть только внешнее сходство.
З.Ы. начала вспоминать методики Занкова, Шаталова и т.д. Что-то есть у меня ощущение, что они как раз сторонники быстрого освоения умножения как операции, и только на выработанном навыке потом учили решать задачи + учили видеть необходимость умножения в задачах.
На мой взгляд, этому треду не хватает картинки
Честно говоря я даже задумался, как же вам, альтернативно одаренным, объяснить, почему вы не правы. Понятно, что не читали тему как раз вы, раз пропустили пример логики 9 первых кусков сахара и 9 вторых кусков сахара. Тогда я понял, в чем ваша проблема - как раз в чашках и кусках сахара. Куски сахара помещаются внутрь чашки, а допустим три яблока принадлежат Пете. Что вы будете делать и как объяснять это "соглашение", если задача такая: в таблице 2 строки и 9 столбцов, сколько клеток в таблице? Ну и какой же множитель "методически" более правильно поставить на первое место? Может ввести "соглашение", что строки главнее столбцов?
Заодно передаю привет офцеводу, который ну просто не может пройти мимо, даже вон, переметнулся на другую сторону. В хоре своем остатки интеллекта растерял, видимо.
Заодно передаю привет офцеводу, который ну просто не может пройти мимо, даже вон, переметнулся на другую сторону. В хоре своем остатки интеллекта растерял, видимо.
Возможно я не права, но мне кажется более полезным обучать принципу умножения как сложения на кубиках рядами и столбиками, сразу понять про перестановку множителей, освоить простое умножение на примерах.Кубики и есть уже умножение в реальной жизни. Ребенку нужно понимать, зачем используется умножение, а это дают только конкретные примеры.
Честно говоря я даже задумался, как же вам, альтернативно одаренным, объяснить, почему вы не правы. Понятно, что не читали тему как раз вы, раз пропустили пример логики 9 первых кусков сахара и 9 вторых кусков сахара. Тогда я понял, в чем ваша проблема - как раз в чашках и кусках сахара. Куски сахара помещаются внутрь чашки, а допустим три яблока принадлежат Пете. Что вы будете делать и как объяснять это "соглашение", если задача такая: в таблице 2 строки и 9 столбцов, сколько клеток в таблице? Ну и какой же множитель "методически" более правильно поставить на первое место? Может ввести "соглашение", что строки главнее столбцов?Послушай. Речь идет об обучении самому понятию "умножение" тех, кто об этом ничего не знает. Твой вопрос про таблицу такой ученик решит просто, он пальцем пересчитает все клетки. И все. Дальше, показав ему, что умножив число строк на число столбцов он получит тоже самое, ты просто дашь ему в руки "магию", применять которую с умом он не сможет. У него будет только таблица, а уже, как посчитать число кусков сахара в чашках, ему будет не понятно, пока ты не разложишь их в таблицу. А задача стоит в том, чтобы дать ребенку понимание, когда следует применять умножение. Именно для этого решается множество одинаковых задач с разными формулировками. Все, что ты пишешь, верно, но не применимо для обучения детей умножению. И я не утверждаю, что на 100% прав. Может и ошибаюсь. Но у меня есть перед глазами сын дошкольник, с которым я регулярно занимаюсь, и все что я тут пишу укладывается в наши занятия. И еще раз повторю, формулировка в методичке бредовая, она ничего не объясняет, а наоборот запутывает.
Что вы будете делать и как объяснять это "соглашение", если задача такая: в таблице 2 строки и 9 столбцов, сколько клеток в таблице?Ты возьми сам эту задачу и начни объяснять её решение гипотетическому ребенку.
Будет это выглядеть примерно так:
Смотрите, дети, с одной стороны, если считать по строчкам, то в каждой строке 9 клеток, а строк 2, поэтому когда мы берем два раза по 9, получаем 18. С другой стороны, можно считать по столбцам: в каждом столбце по 2 клетки, а столбцов всего 9, получаем девять раз по 2. Но клеток-то одинаковое количество, они же те эе самые. Значит не важно как считать, можно вдоль, можно поперек. Это, дети, и называется, переместительный закон умножения...
Так вот в приведенном примере курсивом выделены места, где ты используешь то самое соглашение. Потому что это "соглашение" это просто буквальная запись фразы "столько-то раз по столько-то"
А какой сейчас учебник для 2-ого класса? Интересно взглянуть
Не знаю. У меня дошкольник пока.
> Тем не менее теперь ты предлагаешь учить таблицу умножения (коммутативную!) во втором классе
чтобы учить таблицу умножения, не обязательно использовать знание о его коммуникативности.
> а доказывать коммутативность умножения (что само по себе бред)
доказывать коммуникативность не бред. Напротив, бред — это принимать его на веру. При всём моём уважении к Звонкину, я не мог не потерять пиетет к почтенному педагогу-математику, когда дошёл до места, где он признался, что лишь под конец университета придумал именно то доказательство, которое вообще-то в советской школе давали во втором или третьем классе.
Мне в таких случаях, как этот тред, просто кипящий СЗМом, вспоминается чья-та фраза: "Они верили, что Земля круглая, потому что в детстве видели глобус".
чтобы учить таблицу умножения, не обязательно использовать знание о его коммуникативности.
> а доказывать коммутативность умножения (что само по себе бред)
доказывать коммуникативность не бред. Напротив, бред — это принимать его на веру. При всём моём уважении к Звонкину, я не мог не потерять пиетет к почтенному педагогу-математику, когда дошёл до места, где он признался, что лишь под конец университета придумал именно то доказательство, которое вообще-то в советской школе давали во втором или третьем классе.
Мне в таких случаях, как этот тред, просто кипящий СЗМом, вспоминается чья-та фраза: "Они верили, что Земля круглая, потому что в детстве видели глобус".
2+2+2+2+2+2+2+2+2=18 (2 литра молока от 9 коров)(1+1+1+1+1+1+1+1+1)*2=18
2*(1+1+1+1+1+1+1+1+1)=18
2*9=18
9*2=18
Вопрос в том, какую дистрибутивность вводят в начальной школе: правую, левую или обе.
Но авторы методички в целом правы. Такие понятия как коммутативность и дистрибутивность давно пора вынести из основного курса математики и преподавать в рамках платного спецкурса. Тогда основная масса населения сможет считать только на калькуляторе и не больше 2-3 действий. Представляете сколько профита?
МММ побьет все рекорды. Формулу пенсии поймет 5% населения. 146% вообще никого не смутят.
Твой вопрос про таблицу такой ученик решит просто, он пальцем пересчитает все клетки. И все. Дальше, показав ему, что умножив число строк на число столбцов он получит тоже самое, ты просто дашь ему в руки "магию", применять которую с умом он не сможетМагия умножения ребенком отлично применяется, если он ее понял. Без долгого надрачивания, сразу. Если ребенок этого не понял, значит ему просто рано учить умножение. Не надо мучить ребенка.
Знаю не по наслышке - сама училась умножению когда-то, со мной училось еще 25 человек.
А сейчас во втором классе школы изучают наивную теорию множеств. Очень удивилась, увидев в тетради племяшки-второклассницы диаграммы Эйлера-Венна. Это, на мой взляд, сложнее в плане абстрактого восприятия.
объясни, пожалуйста, без использования коммутативного закона и без использования тавтологичного правила "ответ неправильный получится" почему когда речь идет о задаче:Именно этим в школе и занимаются с первого класса. Вводятся в одном случае симметричные определения "Слагаемое", "Слагаемое" и "Сумма", в другом "Уменьшаемо", "Вычитаемое" и "Разность". Аналогично с умножением. Эти определения с одной стороны органичны с точки зрения языка, с другой намекают на симметричность операции в одном случае и несимметричность в другом.
было 5 птиц, потом из них 3 улетело,
можно писать: 5 - 3, но нельзя писать 3 - 5
а для задачи:
было 5 птиц, потом к ним 3 прилетело,
можно писать: 3 + 5 и 5 + 3
Если ребенок этого не понял, значит ему просто рано учить умножение. Не надо мучить ребенка.Такая логика не выдерживает никакой критики.
"Если ребенок не понимает как из букв прочитать слово, значит ему просто рано учиться читать. Не надо мучить ребенка".
"Если ребенок не понимает, что писаться в штанишки плохо, значит ему еще рано ходить на горшок. Не надо мучить ребенка".
"Если ребенок не понимает, что нельзя бить совочком по голове, значит ему еще рано давать совочек. Не надо мучить ребенка".
убики и есть уже умножение в реальной жизниЯ не так выразилась - искать на других помимо кубиков примерах разное выражение условных чего-то по сколько-то раз. Просто именно в методиках, которые быстро обучают математике, применён такой подход, если я не ошибаюсь - сначала формальная операция, потом поиск её приложений в реальной жизни. Эти методики обучают за меньшее время более полному владению математике примерно то же количество детей, что и при вот таком, как у Белошистой. Т.е. они в итоге более эффективны. Но возможно конкретно в этом я и ошибаюсь - читала состав самих методик в приложении к конкретным темам давно.
Кубики и есть уже умножение в реальной жизни.кстати да. На кубиках ребёнку можно быстро объяснить некоммутативность умножения матриц
Как?
Как?матрицы вращения
чтобы учить таблицу умножения, не обязательно использовать знание о его коммуникативности.Да ну? Думаешь никто не заметит, что таблица симметричная?
доказывать коммуникативность не бред. Напротив, бред — это принимать его на веру.Скажи это тем, кто включает коммутативность умножения в аксиомы формализации арифметики Пеано.
доказательство, которое вообще-то в советской школе давали во втором или третьем классе.
Это не доказательство, а рукомахание.
Скажи это тем, кто включает коммутативность умножения в аксиомы формализации арифметики Пеано.Если ты включаешь, то ты несёшь бред. Потому что развёл кучу аксиом, там где хватило бы нескольких, из которых следуют все остальные как теоремы. Про бритву оккама слыхал, надеюсь?
В двумерном случае коммутируют, кстати.
> Да ну? Думаешь никто не заметит, что таблица симметричная?
Заметит — и молодец. Факт симметричности таблицы, однако, вовсе не требует обязательного преподавания коммутативности умножения для изучения таблицы.
> тем, кто включает коммутативность умножения в аксиомы формализации арифметики Пеано.
ну и каша. Во-первых, аксиомы Пеано не включают коммутативности в явном виде. Во-вторых, в школе не обязательно изучать аксиомы Пеано. Мы их изучали только в 10 или 11 классе, и не могу упомнить случая, чтобы мне впоследствии понадобились эти сакральные знания. Математика как-то успешно обходилась без них до начала XX века, многократно превзойдя весь объём школьной программы и заметный кусок вузовской.
А в-третьих, школьнику не дают задач, где нужны аксиомы Пеано. Не в том смысле, что школьник глупый и обойдётся нестрогими методами. А напротив, в том смысле, что аксиомы Пеано интересны лишь постольку, поскольку, будучи простыми и непротиворечивыми, они одновременно успешно описывают числа, возникающие в задачах о сложении яблок и умножении кусков/чашку на число чашек. Но типичному мехматянину это, конечно, не понять. Никогда не забуду, как мехматянин, полагающий, что в розетке есть плюс и минус, учил меня, что глубинная суть импульса — это производная лагранжиана, а лагранжиан - это такая богом даденная функция, взятая из учебника.
> Это не доказательство, а рукомахание.
Рукомахание — это говорить, что пять яблок на шесть человек и у шести человек по пять яблок дают одинаковый ответ, поскольку таковы аксиомы Пеано. Любопытно, что тот Звонкин, на мой комментарий к которому ты высказал своё веское схоластическое мнение, в итоге остановился как раз на "рукомахательном" доказательстве, напрочь забыв, что именно его в младшей школе и дают.
Заметит — и молодец. Факт симметричности таблицы, однако, вовсе не требует обязательного преподавания коммутативности умножения для изучения таблицы.
> тем, кто включает коммутативность умножения в аксиомы формализации арифметики Пеано.
ну и каша. Во-первых, аксиомы Пеано не включают коммутативности в явном виде. Во-вторых, в школе не обязательно изучать аксиомы Пеано. Мы их изучали только в 10 или 11 классе, и не могу упомнить случая, чтобы мне впоследствии понадобились эти сакральные знания. Математика как-то успешно обходилась без них до начала XX века, многократно превзойдя весь объём школьной программы и заметный кусок вузовской.
А в-третьих, школьнику не дают задач, где нужны аксиомы Пеано. Не в том смысле, что школьник глупый и обойдётся нестрогими методами. А напротив, в том смысле, что аксиомы Пеано интересны лишь постольку, поскольку, будучи простыми и непротиворечивыми, они одновременно успешно описывают числа, возникающие в задачах о сложении яблок и умножении кусков/чашку на число чашек. Но типичному мехматянину это, конечно, не понять. Никогда не забуду, как мехматянин, полагающий, что в розетке есть плюс и минус, учил меня, что глубинная суть импульса — это производная лагранжиана, а лагранжиан - это такая богом даденная функция, взятая из учебника.
> Это не доказательство, а рукомахание.
Рукомахание — это говорить, что пять яблок на шесть человек и у шести человек по пять яблок дают одинаковый ответ, поскольку таковы аксиомы Пеано. Любопытно, что тот Звонкин, на мой комментарий к которому ты высказал своё веское схоластическое мнение, в итоге остановился как раз на "рукомахательном" доказательстве, напрочь забыв, что именно его в младшей школе и дают.
В двумерном случае коммутируют, кстати.двумерные кубики должны называться как-то по-другому, не кубиками
Это не доказательство, а рукомахание.Речь не о доказательстве свойств формальной математической операции, а о доказательстве того факта, что операция должна обладать такими свойствам, чтобы отвечать практическим нуждам. Далее свойство приписывается операции аксиоматически. А детям это знать вообще не обязательно.
Если ты включаешь, то ты несёшь бред. Потому что развёл кучу аксиом, там где хватило бы нескольких, из которых следуют все остальные как теоремы.Это называется разные формализации. Можно написать один набор аксиом, а можно и другой набор аксиом, который будет эквивалентен. Почему так делают? Потому что разные наборы удобнее для разных ситуаций.
Будет это выглядеть примерно так:Смотрите, дети, с одной стороны, если считать по строчкам, то в каждой строке 9 клеток, а строк 2, поэтому когда мы берем два раза по 9, получаем 18. С другой стороны, можно считать по столбцам: в каждом столбце по 2 клетки, а столбцов всего 9, получаем девять раз по 2. Но клеток-то одинаковое количество, они же те эе самые. Значит не важно как считать, можно вдоль, можно поперек. Это, дети, и называется, переместительный закон умножения...и значит вы можете расставлять множители как вам захочется, а нехорошую тетю белошистую и некоторых особо умных из МГУ можете смело слать на ... хотя нет, последнее слово я бы детям говорить не стал.
Дети - не компы. Ты не можешь загрузить в ребенка пачку алгоритмов и рассчитывать, что с этого момента он будет им следовать. Сам процесс осознания того, что "расставлять множители можно как захочется" занимает не один месяц. Не говоря уже об осознании того, что такое множитель и вообще число.
Да, если ты знаешь, что вот этот конкретный ребенок уже всё понял, то ему методические "подпорки" не нужны и часто они его наоборот только зря ограничивают. Ему нужно именно что объяснить их вспомогательность и необязательность. Но это не значит, что они вообще не нужны никогда, никому и ни при каких условиях.
Да, если ты знаешь, что вот этот конкретный ребенок уже всё понял, то ему методические "подпорки" не нужны и часто они его наоборот только зря ограничивают. Ему нужно именно что объяснить их вспомогательность и необязательность. Но это не значит, что они вообще не нужны никогда, никому и ни при каких условиях.
значит вы можете расставлять множители как вам захочется
Вообще-то следует только то, что можно как угодно"расставлять" при подсчёте (если считать через повторное сложение) или, что то же самое, учить только половину таблицы умножения.
Как нужно записывать решение задачки в тетради — отсюда не следует.
я хочу что сказать, можно долго спорить, насколько нужно/не нужно формализовывать и заставлять/наказывать за 2*9 или 9*2, но одно я скажу точно, если бы я мог, избежав ответственности, уебать тому, кто этот бред придумал в виде учебника/пособия и тому, кто его форсит- сделал бы это без оглядки.
а что тебя останавливает?
Смотрите, дети, с одной стороны, если считать по строчкам, то в каждой строке 9 клеток, а строк 2, поэтому когда мы берем два раза по 9, получаем 18. С другой стороны, можно считать по столбцам: в каждом столбце по 2 клетки, а столбцов всего 9, получаем девять раз по 2.А девять раз по два - это 9*2 или 2*9?
А по два девять раз?
Вот, тут avva написал.
http://avva.livejournal.com/2608125.html
Но более интересно в следующем посте
-----------------------------
Об этой истории уже написаны десятки записей и тысячи комментариев, и я не собирался к ним ничего добавлять, но пришло в голову несколько соображений, которые вроде бы в других местах не видел (хотя все тысячи комментариев не читал и решил поделиться.
История в двух словах для тех, кто не слышал: выложили, как учитель поставил тройку за "неправильный" порядок множителей. В задаче "Фермер продал 9 покупателям по 2л. молока, сколько всего молока он продал?" школьница написала 9*2=18, а учитель перечеркнул, написал, что надо 2*9=18, и поставил тройку.
В комментариях, которых тысячи, мнения разделились на тех, кто возмущается идиотизмом учителя, и тех, кто неожиданно его защищает, и говорит, что если два литра умножить на девять человек, то в ответе будет 18 литров, как надо, а если девять человек на два литра, то в ответе будет 18 человек. В поддержку этой теории обнаружились цитаты из учебников арифметики и методичек; в свою очередь те, кто возмущаются этой оценкой, распостраняют это возмущение также на эти цитаты и их защитников.
Впрочем, есть более сильный аргумент "за учителя", и правильным будет его привести, не ограничиваясь довольно дурацким (на мой взгляд) аргументом, описанным выше. Более сильный аргумент состоит в том, что для того, чтобы дети как следует поняли смысл умножения и его связь с сложением, полезно заставить их заучить фиксированный порядок множителей: 2*9 это 2+2+2... девять раз, а ни в коем случае не 9+9 два раза. И только потом, на более позднем уроке, объяснить им, что порядок на самом деле не имеет значения, и это то же самое.
Те, которые возмущаются, смотрят на это, как на начетничество, считают, что зазубривать такой фиксированный порядок нелепо и ничему не помогает, и говорят, что в любом случае это не оправдывает снижения оценки за правильный ответ.
Мое мнение - за тех, кто "против учителя" и против начетничества. Но об этом подробно говорить уже по-моему бессмысленно (написаны километры за и против); я бы хотел внимательнее приглядеться к аргументу, выделенному выше курсивом. Повторю его тут:
если 2 литра умножить на 9 человек, то в ответе будет 18 литров, а если 9 человек на 2 литра, то в ответе будет 18 человек
Практически теми же словами это сказано в методичке для учителей, ссылка на которую есть выше. Откуда взялось такое убеждение в учебниках арифметики и методичках? Тут надо сослаться на любопытный анализ
biglebowsky (стоит прочитать его целиком который представляет это как "альтернативное умножение":
biglebowsky. Если мы всегда смотрим только на первый множитель, почему в произведении оказываются не метры, а квадратные метры?
Хорошо, а как противники учителя анализируют размерность в произведении, т.е. почему действительно, если порядок умножения не важен, 2 литра умножить на 9 человек получается 18 именно литров, а не человек? Потому что, говорят они совершенно резонно, на самом деле это не "2 литра умножить на 9 человек", а "2 литра/человек умножить на 9 человек". Действительно, продают по два литра на человека, т.е. 2 л/ч, и при умножении этого на 9 человек люди сокращаются и остаются одни литры - а в каком порядке умножать, неважно.
До сих пор был краткий пересказ того, что уже написано на эту тему, дальше идут мои соображения. Я решил поискать в англоязычных учебниках следы того же подхода к размерности произведения, следы этого "альтернативного умножения", используя терминологиюbiglebowsky. И нашел примеры этого в учебниках 19 века, так что это совсем не российское/советское изобретение. Вот два примера:
1. Книга "Arithmetic & its Applications", D.P.Colburn, 1856. Раздел под названием "Multiplication", стр. 76 и далее. Обратите внимание, что четко разделены multiplicand и multiplier, соответствующие в русской терминологии множимому и множителю. Любопытно, что "нормативный" порядок в этой книге противопожен русскому! По-русски учебники, которые настаивают на нормативном порядке, в записи 2*9 определяют 2 как множимое, 9 как множитель, а смысл действия как 'взять 2 девять раз'. Тут наоборот 2*9 означает "взять 9 два раза", и это вполне логично, потому что словами это говорится "2 times 9", т.е. дословно именно "два раза девять".
На странице 79 мы читаем:
2. В другой книге, "The Complete Algebra", Edward Olney (1870 порядок множимого и множителя другой, такой, как по-русски, но суть та же. На странице 50 все написано. В этом учебнике запись "2 x 9" означает словами "nine times two", т.е. множимое, multiplicand, пишется всегда первым, как в русских учебниках. И черным по белому написано: множитель всегда должен быть безразмерным числом. Можно умножить $12 на 5, но как умножить $12 на $5? - это же абсурд.
Отмечу, что я не слишком глубоко копал и не знаю, действительно ли процитированный выше из двух учебников подход был стандартным в описании умножения в 19-м веке по-английски. Если кто-то хочет найти еще примеры и сравнить, то буду рад узнать результаты ваших поисков. Но как минимум это демонстрирует, что этот подход был вполне обычным, и не был придуман в России или СССР.
Напрашивается вопрос, как же в таком случае эти книги рассматривают примеры, когда действительно надо умножать одно размерное число на другое? Например, площадь комнаты размером 6 метров на 6 метров? Во второй из вышепроцитированных книг геометрии нет вообще, но в первой есть определение единицы площади ("square measure" и целый раздел задач на измерение ("mensuration" в котором все время умножаются длины. Как же книга это объясняет?
Если честно, я сам до конца не понимаю, это не очень хорошо объяснено, но мне это представляется примерно так. Там, где мы скажем "6 метров умножить * 6 метров = 36 квадратных метра", этот учебник скажет следующее. Есть единица площади, квадратный метр, которую мы представляем вполне геометрически (квадрат размером 1x1 и чтобы узнать, сколько квадратных метров входит в квадрат размером 6 метров на 6 метров, нужно его длину умножить на его ширину, и результат будет вот это число квадратных метров. Т.е. сама операция умножения происходит с безразмерными числами 6 и 6, и мы заранее решили, какая будет размерность результата. Мы не умножаем 6 метров на 6 метров, умножать можно только безразмерные числа или одно размерное число на безразмерное. Так, мне кажется, они это объясняют (прямая цитата, стр. 35: "...and generally any surface must contain as many square units as there are in the product obtained by multiplying its length by its breadth").
Я остановлюсь пока на этом, и в следующей записи перейду к тому, что на самом деле интересно для меня - откуда взялся этот подход, и сравнение его с тем вычислением размерностей, которое нам привычно и логично.
http://avva.livejournal.com/2608125.html
Но более интересно в следующем посте
-----------------------------
Об этой истории уже написаны десятки записей и тысячи комментариев, и я не собирался к ним ничего добавлять, но пришло в голову несколько соображений, которые вроде бы в других местах не видел (хотя все тысячи комментариев не читал и решил поделиться.
История в двух словах для тех, кто не слышал: выложили, как учитель поставил тройку за "неправильный" порядок множителей. В задаче "Фермер продал 9 покупателям по 2л. молока, сколько всего молока он продал?" школьница написала 9*2=18, а учитель перечеркнул, написал, что надо 2*9=18, и поставил тройку.
В комментариях, которых тысячи, мнения разделились на тех, кто возмущается идиотизмом учителя, и тех, кто неожиданно его защищает, и говорит, что если два литра умножить на девять человек, то в ответе будет 18 литров, как надо, а если девять человек на два литра, то в ответе будет 18 человек. В поддержку этой теории обнаружились цитаты из учебников арифметики и методичек; в свою очередь те, кто возмущаются этой оценкой, распостраняют это возмущение также на эти цитаты и их защитников.
Впрочем, есть более сильный аргумент "за учителя", и правильным будет его привести, не ограничиваясь довольно дурацким (на мой взгляд) аргументом, описанным выше. Более сильный аргумент состоит в том, что для того, чтобы дети как следует поняли смысл умножения и его связь с сложением, полезно заставить их заучить фиксированный порядок множителей: 2*9 это 2+2+2... девять раз, а ни в коем случае не 9+9 два раза. И только потом, на более позднем уроке, объяснить им, что порядок на самом деле не имеет значения, и это то же самое.
Те, которые возмущаются, смотрят на это, как на начетничество, считают, что зазубривать такой фиксированный порядок нелепо и ничему не помогает, и говорят, что в любом случае это не оправдывает снижения оценки за правильный ответ.
Мое мнение - за тех, кто "против учителя" и против начетничества. Но об этом подробно говорить уже по-моему бессмысленно (написаны километры за и против); я бы хотел внимательнее приглядеться к аргументу, выделенному выше курсивом. Повторю его тут:
если 2 литра умножить на 9 человек, то в ответе будет 18 литров, а если 9 человек на 2 литра, то в ответе будет 18 человек
Практически теми же словами это сказано в методичке для учителей, ссылка на которую есть выше. Откуда взялось такое убеждение в учебниках арифметики и методичках? Тут надо сослаться на любопытный анализ
biglebowsky (стоит прочитать его целиком который представляет это как "альтернативное умножение":Оказалось, что огромное количество людей пользуется неким альтернативным умножением по следующей методике:Другой способ сказать примерно то же самое - это что мы рассматриваем все множители, кроме первого, как безразмерные. То есть не "два литра умножить на девять человек", а "два литра умножить на девять", и не "девять человек на два литра", а "девять человек на два". В такой форме утверждение защитников учителя даже начинает выглядеть резонным, потому что размерности совпадают: 2л*9=18л, 9ч*2=18ч, и "выходит", что неправильно писать 9*2. Однако на это можно возразить: но почему не сказать 9*2л=18л? В ответ на это защитники учителя говорят: потому что порядок важен, и первой в умножении мы всегда пишем "размерную" величину - литры, человеки, что угодно еще, а второй безразмерную, т.е. 'разы'. Почему так - потому что так проявляется связь с сложением, см. выше. С другой стороны, как при таком подходе понять вычисление площади комнаты размером 6 метров на 6 метров, совершенно непонятно, как справедливо замечает
"В качестве размерности произведения берем размерность первого множителя, т.е., все размерности, упомянутые после первого множителя, из рассмотрения выбрасываем."
biglebowsky. Если мы всегда смотрим только на первый множитель, почему в произведении оказываются не метры, а квадратные метры?Хорошо, а как противники учителя анализируют размерность в произведении, т.е. почему действительно, если порядок умножения не важен, 2 литра умножить на 9 человек получается 18 именно литров, а не человек? Потому что, говорят они совершенно резонно, на самом деле это не "2 литра умножить на 9 человек", а "2 литра/человек умножить на 9 человек". Действительно, продают по два литра на человека, т.е. 2 л/ч, и при умножении этого на 9 человек люди сокращаются и остаются одни литры - а в каком порядке умножать, неважно.
До сих пор был краткий пересказ того, что уже написано на эту тему, дальше идут мои соображения. Я решил поискать в англоязычных учебниках следы того же подхода к размерности произведения, следы этого "альтернативного умножения", используя терминологию
biglebowsky. И нашел примеры этого в учебниках 19 века, так что это совсем не российское/советское изобретение. Вот два примера:1. Книга "Arithmetic & its Applications", D.P.Colburn, 1856. Раздел под названием "Multiplication", стр. 76 и далее. Обратите внимание, что четко разделены multiplicand и multiplier, соответствующие в русской терминологии множимому и множителю. Любопытно, что "нормативный" порядок в этой книге противопожен русскому! По-русски учебники, которые настаивают на нормативном порядке, в записи 2*9 определяют 2 как множимое, 9 как множитель, а смысл действия как 'взять 2 девять раз'. Тут наоборот 2*9 означает "взять 9 два раза", и это вполне логично, потому что словами это говорится "2 times 9", т.е. дословно именно "два раза девять".
На странице 79 мы читаем:
NOTE: In changing the order of factors the one taken for the multiplier should always be regarded as an abstract number (see 74g) the other should take the denomination of the original multiplicand. Thus 4 times 3 apples = 12 apples etc.Здесь "abstract number" как раз означает безразмерное число, а "denomination" - размерность (литры, человеки итд.). То есть, если следовать этим правилам и применить их к задаче про 18 литров, как раз надо записать 9 * 2 литра = 18 литров, но никак на 2 литра * 9 = 18 литров - это неправильно, потому что первый множитель это всегда число "раз", абстрактное, безразмерное число.
2. В другой книге, "The Complete Algebra", Edward Olney (1870 порядок множимого и множителя другой, такой, как по-русски, но суть та же. На странице 50 все написано. В этом учебнике запись "2 x 9" означает словами "nine times two", т.е. множимое, multiplicand, пишется всегда первым, как в русских учебниках. И черным по белому написано: множитель всегда должен быть безразмерным числом. Можно умножить $12 на 5, но как умножить $12 на $5? - это же абсурд.
Отмечу, что я не слишком глубоко копал и не знаю, действительно ли процитированный выше из двух учебников подход был стандартным в описании умножения в 19-м веке по-английски. Если кто-то хочет найти еще примеры и сравнить, то буду рад узнать результаты ваших поисков. Но как минимум это демонстрирует, что этот подход был вполне обычным, и не был придуман в России или СССР.
Напрашивается вопрос, как же в таком случае эти книги рассматривают примеры, когда действительно надо умножать одно размерное число на другое? Например, площадь комнаты размером 6 метров на 6 метров? Во второй из вышепроцитированных книг геометрии нет вообще, но в первой есть определение единицы площади ("square measure" и целый раздел задач на измерение ("mensuration" в котором все время умножаются длины. Как же книга это объясняет?
Если честно, я сам до конца не понимаю, это не очень хорошо объяснено, но мне это представляется примерно так. Там, где мы скажем "6 метров умножить * 6 метров = 36 квадратных метра", этот учебник скажет следующее. Есть единица площади, квадратный метр, которую мы представляем вполне геометрически (квадрат размером 1x1 и чтобы узнать, сколько квадратных метров входит в квадрат размером 6 метров на 6 метров, нужно его длину умножить на его ширину, и результат будет вот это число квадратных метров. Т.е. сама операция умножения происходит с безразмерными числами 6 и 6, и мы заранее решили, какая будет размерность результата. Мы не умножаем 6 метров на 6 метров, умножать можно только безразмерные числа или одно размерное число на безразмерное. Так, мне кажется, они это объясняют (прямая цитата, стр. 35: "...and generally any surface must contain as many square units as there are in the product obtained by multiplying its length by its breadth").
Я остановлюсь пока на этом, и в следующей записи перейду к тому, что на самом деле интересно для меня - откуда взялся этот подход, и сравнение его с тем вычислением размерностей, которое нам привычно и логично.
http://avva.livejournal.com/2608151.html
Эта запись продолжает предыдущую "о литрах, людях и умножении" - начните с нее, если еще не читали.
Сейчас я расскажу вам, что я лично для себя нового понял из всей этой истории. Не знаю, как для вас, а для меня это понимание было совершенно неожиданным, даже ошеломительным. Я думал, что все понимаю в задаче про 18 литров и вычислении размерностей, а оказалось, что самое важное понимаю не до конца.
Я сидел и читал довольно долго отрывки из разных учебников арифметики 19 века вчера, некоторые из которых процитировал в прошлой записи. И все не мог понять, зачем же им нужны эти странные правила, что только множимое может быть конкретным (литры, люди, метры, доллары а множитель обязательно абстрактным (разы)? Ведь действительно, самый простой способ записать пример с литрами, чтобы все размерности сходились - это
"2л/ч * 9ч = 18л". Тут все учтено и все логично, и ведь сказано в условии, что по два литра на человека. Или возьмите другой тривиальный пример, который приводили: машина едет 2 часа со скоростью 60 км/ч. Сколько она проехала? Понятно же, что 2ч * 60км/ч = 60км/ч * 2ч = 120км, порядок значения не имеет, часы в любом случае сокращаются и размерности обоих множителей важны для этого. А если по этим книгам 19 века, то непонятно даже, как это записать логично. Почему же они так извращались?
Я вам сейчас задам несколько риторических вопросов, а вы в них вдумайтесь, как следует, не отвергайте как глупые сразу, ладно?
Машина едет со скоростью 60 километров в час. Или, как мы записываем, 60 км/ч. Единица измерения - единица скорости - км/ч.
Скажите, друзья, а что это такое - поделить километр на час? Какой у этого действия смысл? Когда это вы такое видели? Я знаю, что такое поделить километр на 10 равных частей, например. Поделить пирог на три куска. Поделить 18 на 3. Это все я понимаю. А что такое "поделить километр на час"?
Фермер продал 9 покупателям по 2 литра на человека, мы записываем 2 л/чел * 9чел = 18л. Извините, а что это такое "л/чел"? Как это - поделить литр на человека? Как вы себе такое представляете?
Я знаю, что такое километр в час, это значит, что одному часу соответствует один километр. Но я не знаю, что такое километр поделить на час. Я знаю, что такое литр на человека, это значит, что один человек получает один литр. Но я не знаю, что такое литр поделить на человека, если пользоваться тем понятием 'деление', которое мы знаем из арифметики. То, в котором можно поделить пирог на троих или 10 на 2.
Но мы говорим вслух "километр в час", а записываем км/ч. Говорим вслух "литр на человека", а записываем л/ч. Я осознал, что я это делаю, не задумываясь ни на секунду о том, что это несколько разные вещи. Я предлагаю вам продумать это, как следует - ведь это прекрасно совершенно, мы постоянно пишем бессмыслицу, не задумываясь об этом! (я преувеличиваю ради риторики, это не бессмыслица, конечно, но можно так на это посмотреть). Все эти км/ч - что это такое вообще?
"км/ч" - это использование, повседневное и незаметное, метода размерностей. "км/ч" - это такой способ записать алгебраически обычное и понятное "километр в час", чтобы потом обычными правилами умножения этих абстрактных единиц все "правильно сократилось". Когда мы записываем 60 км/ч * 2 ч = 120 км, то все удобно сокращается, потому что мы так специально подстроили, записав км/ч в виде дроби. По природе своей в этом понятии скорости нет дроби в арифметическом смысле, нет деления, как мы его знаем из арифметики.
Каковы на самом деле единицы скорости, что такое "60 километров в час"? Это фиксирование определенного масштабирования, определенного способа совместить шкалу "километры" и шкалу "часы". В этом нет ничего от "деления", но у этой операции общие свойства с делением. Если мы берем сколько-то "километров в час" и умножаем их на сколько-то "часов", то в результате будут только "километры". Это раз. Более того, если мы изменим масштаб километров (перейдем в метры, скажем то скорость изменится в одну сторону, а если изменим масштаб часов, то в другую (километры в метры - скорость увеличится; часы в секунды - уменьшится). Это ровно то, что происходит с делением: если делитель увеличить, частное увеличится, делимое увеличить - частное уменьшится. Выходит, что эту операцию фиксации масштаба, операцию "в,на", удобно записать в виде деления "км/ч", и все единицы размерности будут себя вести ровно так, как нам надо.
Но кто-то должен был это придумать. Это не очевидно "просто так", что можно взять и записать "километр в час" как км/ч. И я не знаю, когда это придумали, но в 19-м веке, судя по всему, так не делали! Я просмотрел, например, несколько учебников механики 19 века. Когда там описывается скорость, везде пишут "feet per second" итд., нигде ни разу не написано "f/s" или m/s или еще как. Нам кажется странным, что они так не писали, а с их точки зрения, вполне резонной, это же полный бред: как можно метры поделить на секунду, зачем писать такую чепуху?
(да, они умели, конечно, оперировать многочленами, и понимали, что такое x/y. Но зачем, с их точки зрения, относиться к конкретным метрам и секундам как к неизвестным величинам x и y? Опять-таки, бред какой-то).
В "Британнике" за 1911 год я прочитал статью о единицах измерения, и там сказано, что метод размерностей впервые был сформулирован в 1822 году, в книге Фурье "Аналитическая теория тепла". Вот соответствующий раздел этой книги в английском переводе (раздел "General remarks"). Фурье объясняет там, что в каждом физическом уравнении размерности длины/времени/температуры/итд. с двух сторон должны быть одинаковыми, и этим удобно пользоваться. Но он не пишет, как написали бы мы сейчас, что если слева m/s^2, то и справа должно быть m/s^2. Он не делит метры на секунды! Он пишет, что в такой ситуации у длины есть экспонента +1 с обеих сторон уравнения, а у времени экспонента -2. И объясняет, что это значит, с точки зрения перехода на другие единицы (скажем, если экспонента длины +1, то увеличив длину в 10 раз, мы увеличим значение в 10 раз, а если -1, то уменьшим в 10 раз). Но ему не приходит в голову взять эти единицы размерности и записать их делением (или умножением!). Это определенный дополнительный абстрактный шаг, который кто-то когда-то придумал позже, возможно, в конце 19-го века или даже начале 20-го. Я бы хотел проследить, кто и когда (если у вас есть идеи, поделитесь).
И вот это меня ошеломило, на самом деле - что столь очевидное для меня км/ч или л/чел или что угодно еще на самом деле даже в конце 19-го века не использовалось широко, и всего за последние 100 лет так твердо вошло в наш математический язык, что школьники сейчас пользуются этим, не задумываясь ни на секунду.
Но вот что следует признать из всего этого, и опять-таки мне это было нетривиально понять - что как минимум школьникам в младших классах, которым только объясняют, что такое умножение, объяснять "2 л/чел * 9 чел" было бы совершенно неправильно. Нам эти 2л/чел кажутся совершенно прозрачным способом написать "2 литра на человека", но на самом деле это нетривиальная абстракция (до которой в 19-м веке не додумались! в определенном смысле "нечестное" использование деления - которого эти школьники вообще еще не знают - для того, чтобы сошлись размерности. Это не значит, что я согласен с защитниками того самого учителя, нет; все равно и 2*9, и 9*2 надо считать правильным ответом. Но до того, как я обо всем этом как следует подумал, я бы наивно предложил объяснить детям про 2л/чел, а теперь понимаю, что это куда сложнее, чем материал "что такое умножение", который они проходят.
Эта запись продолжает предыдущую "о литрах, людях и умножении" - начните с нее, если еще не читали.
Сейчас я расскажу вам, что я лично для себя нового понял из всей этой истории. Не знаю, как для вас, а для меня это понимание было совершенно неожиданным, даже ошеломительным. Я думал, что все понимаю в задаче про 18 литров и вычислении размерностей, а оказалось, что самое важное понимаю не до конца.
Я сидел и читал довольно долго отрывки из разных учебников арифметики 19 века вчера, некоторые из которых процитировал в прошлой записи. И все не мог понять, зачем же им нужны эти странные правила, что только множимое может быть конкретным (литры, люди, метры, доллары а множитель обязательно абстрактным (разы)? Ведь действительно, самый простой способ записать пример с литрами, чтобы все размерности сходились - это
"2л/ч * 9ч = 18л". Тут все учтено и все логично, и ведь сказано в условии, что по два литра на человека. Или возьмите другой тривиальный пример, который приводили: машина едет 2 часа со скоростью 60 км/ч. Сколько она проехала? Понятно же, что 2ч * 60км/ч = 60км/ч * 2ч = 120км, порядок значения не имеет, часы в любом случае сокращаются и размерности обоих множителей важны для этого. А если по этим книгам 19 века, то непонятно даже, как это записать логично. Почему же они так извращались?
Я вам сейчас задам несколько риторических вопросов, а вы в них вдумайтесь, как следует, не отвергайте как глупые сразу, ладно?
Машина едет со скоростью 60 километров в час. Или, как мы записываем, 60 км/ч. Единица измерения - единица скорости - км/ч.
Скажите, друзья, а что это такое - поделить километр на час? Какой у этого действия смысл? Когда это вы такое видели? Я знаю, что такое поделить километр на 10 равных частей, например. Поделить пирог на три куска. Поделить 18 на 3. Это все я понимаю. А что такое "поделить километр на час"?
Фермер продал 9 покупателям по 2 литра на человека, мы записываем 2 л/чел * 9чел = 18л. Извините, а что это такое "л/чел"? Как это - поделить литр на человека? Как вы себе такое представляете?
Я знаю, что такое километр в час, это значит, что одному часу соответствует один километр. Но я не знаю, что такое километр поделить на час. Я знаю, что такое литр на человека, это значит, что один человек получает один литр. Но я не знаю, что такое литр поделить на человека, если пользоваться тем понятием 'деление', которое мы знаем из арифметики. То, в котором можно поделить пирог на троих или 10 на 2.
Но мы говорим вслух "километр в час", а записываем км/ч. Говорим вслух "литр на человека", а записываем л/ч. Я осознал, что я это делаю, не задумываясь ни на секунду о том, что это несколько разные вещи. Я предлагаю вам продумать это, как следует - ведь это прекрасно совершенно, мы постоянно пишем бессмыслицу, не задумываясь об этом! (я преувеличиваю ради риторики, это не бессмыслица, конечно, но можно так на это посмотреть). Все эти км/ч - что это такое вообще?
"км/ч" - это использование, повседневное и незаметное, метода размерностей. "км/ч" - это такой способ записать алгебраически обычное и понятное "километр в час", чтобы потом обычными правилами умножения этих абстрактных единиц все "правильно сократилось". Когда мы записываем 60 км/ч * 2 ч = 120 км, то все удобно сокращается, потому что мы так специально подстроили, записав км/ч в виде дроби. По природе своей в этом понятии скорости нет дроби в арифметическом смысле, нет деления, как мы его знаем из арифметики.
Каковы на самом деле единицы скорости, что такое "60 километров в час"? Это фиксирование определенного масштабирования, определенного способа совместить шкалу "километры" и шкалу "часы". В этом нет ничего от "деления", но у этой операции общие свойства с делением. Если мы берем сколько-то "километров в час" и умножаем их на сколько-то "часов", то в результате будут только "километры". Это раз. Более того, если мы изменим масштаб километров (перейдем в метры, скажем то скорость изменится в одну сторону, а если изменим масштаб часов, то в другую (километры в метры - скорость увеличится; часы в секунды - уменьшится). Это ровно то, что происходит с делением: если делитель увеличить, частное увеличится, делимое увеличить - частное уменьшится. Выходит, что эту операцию фиксации масштаба, операцию "в,на", удобно записать в виде деления "км/ч", и все единицы размерности будут себя вести ровно так, как нам надо.
Но кто-то должен был это придумать. Это не очевидно "просто так", что можно взять и записать "километр в час" как км/ч. И я не знаю, когда это придумали, но в 19-м веке, судя по всему, так не делали! Я просмотрел, например, несколько учебников механики 19 века. Когда там описывается скорость, везде пишут "feet per second" итд., нигде ни разу не написано "f/s" или m/s или еще как. Нам кажется странным, что они так не писали, а с их точки зрения, вполне резонной, это же полный бред: как можно метры поделить на секунду, зачем писать такую чепуху?
(да, они умели, конечно, оперировать многочленами, и понимали, что такое x/y. Но зачем, с их точки зрения, относиться к конкретным метрам и секундам как к неизвестным величинам x и y? Опять-таки, бред какой-то).
В "Британнике" за 1911 год я прочитал статью о единицах измерения, и там сказано, что метод размерностей впервые был сформулирован в 1822 году, в книге Фурье "Аналитическая теория тепла". Вот соответствующий раздел этой книги в английском переводе (раздел "General remarks"). Фурье объясняет там, что в каждом физическом уравнении размерности длины/времени/температуры/итд. с двух сторон должны быть одинаковыми, и этим удобно пользоваться. Но он не пишет, как написали бы мы сейчас, что если слева m/s^2, то и справа должно быть m/s^2. Он не делит метры на секунды! Он пишет, что в такой ситуации у длины есть экспонента +1 с обеих сторон уравнения, а у времени экспонента -2. И объясняет, что это значит, с точки зрения перехода на другие единицы (скажем, если экспонента длины +1, то увеличив длину в 10 раз, мы увеличим значение в 10 раз, а если -1, то уменьшим в 10 раз). Но ему не приходит в голову взять эти единицы размерности и записать их делением (или умножением!). Это определенный дополнительный абстрактный шаг, который кто-то когда-то придумал позже, возможно, в конце 19-го века или даже начале 20-го. Я бы хотел проследить, кто и когда (если у вас есть идеи, поделитесь).
И вот это меня ошеломило, на самом деле - что столь очевидное для меня км/ч или л/чел или что угодно еще на самом деле даже в конце 19-го века не использовалось широко, и всего за последние 100 лет так твердо вошло в наш математический язык, что школьники сейчас пользуются этим, не задумываясь ни на секунду.
Но вот что следует признать из всего этого, и опять-таки мне это было нетривиально понять - что как минимум школьникам в младших классах, которым только объясняют, что такое умножение, объяснять "2 л/чел * 9 чел" было бы совершенно неправильно. Нам эти 2л/чел кажутся совершенно прозрачным способом написать "2 литра на человека", но на самом деле это нетривиальная абстракция (до которой в 19-м веке не додумались! в определенном смысле "нечестное" использование деления - которого эти школьники вообще еще не знают - для того, чтобы сошлись размерности. Это не значит, что я согласен с защитниками того самого учителя, нет; все равно и 2*9, и 9*2 надо считать правильным ответом. Но до того, как я обо всем этом как следует подумал, я бы наивно предложил объяснить детям про 2л/чел, а теперь понимаю, что это куда сложнее, чем материал "что такое умножение", который они проходят.
Но вот что следует признать из всего этого, и опять-таки мне это было нетривиально понять - что как минимум школьникам в младших классах, которым только объясняют, что такое умножение, объяснять "2 л/чел * 9 чел" было бы совершенно неправильно. Нам эти 2л/чел кажутся совершенно прозрачным способом написать "2 литра на человека", но на самом деле это нетривиальная абстракция (до которой в 19-м веке не додумались!)Ошибочная логика. До десятичной системы счисление люди несколько тысяч лет записывали числа через жопу. Значит десятичная система нетривиальна. Тем не менее десятичной системе учат с первого класса и это правильно.
Так не только потому что так долго не делали.
> Ну и где коммутативность, ассоциативность и прочее?
> Всё нужно доказывать по индукции.
Доказывать нужно только для того, чтобы доказать, что эти акиомы
правильно описывают арифметику, уже знакомую и достаточно хорошо известную.
Потому что аксиомы Пеано --- это аксиоматизация арифметики, а не её построение.
---
"Разве было бы плохо перевернуть перевёрнутый мир?"
> Всё нужно доказывать по индукции.
Доказывать нужно только для того, чтобы доказать, что эти акиомы
правильно описывают арифметику, уже знакомую и достаточно хорошо известную.
Потому что аксиомы Пеано --- это аксиоматизация арифметики, а не её построение.
---
"Разве было бы плохо перевернуть перевёрнутый мир?"
> Роботы + дистанционное обучение?
http://www.technologyreview.com/news/506466/given-tablets-bu...
---
Dr. Gall: Nebesa, to jich přibylo!
Domin: Robotů?
Dr. Gall: Ano.
http://www.technologyreview.com/news/506466/given-tablets-bu...
---
Dr. Gall: Nebesa, to jich přibylo!
Domin: Robotů?
Dr. Gall: Ano.
> И вот это меня ошеломило, на самом деле - что столь
> очевидное для меня км/ч или л/чел или что угодно еще
> на самом деле даже в конце 19-го века не использовалось
> широко, и всего за последние 100 лет так твердо вошло в
> наш математический язык, что школьники сейчас пользуются
> этим, не задумываясь ни на секунду.
Это утверждение ошибочно. Особенно удивительно, что именно тебе это не очевидно, потому что на нашей-то кафедре анализу размерностей придавали большое значение (хотя вообще-то базовый материал проходили все: он даётся в 11 главе первого тома Сивухина).
Уже сто лет как активно применяется именно метод анализа размерностей: рассматриваются комбинации размерности входных параметров, удовлетворяющие размерности выходного, и размерности анализируются отдельно и до величин. Если говорить о предпосылках развития этого метода, то среди влиятельных работ называют статью Рейнольдса 1883 года. В 1880-90-х годах был ряд работ разных авторов, рассматривавших размерность в отрыве от величин. В 1914 году уже была сформулирована П-теорема, применявшаяся без явной формулировки и раньше.
Таким образом, во-первых, метод размерностей насчитывает уже не 100, а примерно 140 лет.
Если кому-то кажется, что это мало, то вспомните, что 200 лет назад не было уверенности, что вещества состоят из молекул, что тепло - это форма энергии, не было понятия модуля числа, впервые появились химические формулы (в виде трудно читаемых картинок: но ведь и о молекулах тогда консенсуса не было, едва только закон кратных отношений открыли не знали о связи магнетизма и электричества и только-только познакомились с ламарковской концепцией эволюции. Что, это теперь нельзя проходить в школе? Что растениям нужны определённые минеральные вещества, было открыто лишь в 1804 году, причём какие именно — узнали лет 30 спустя. Теперь это проходят в младших классах на уроках природоведения. Фоторецепторы были открыты в 1830-х, а роль колбочек в цветоразличении (о которой догазывались ещё с XIX века) была экспериментально показана лишь в 1950-х годах, что не мешает изучать колбочки на уроках ознакомления с окружающим миром. Да о чём говорить, микробная теория болезней зародилась одновременно с теорией размерностей в начале XIX века и была массово принята в науке тоже одновременно с анализом размерностей: в конце XIX века. Сейчас это рассказывают трёхлетним детям.
И во-вторых. Анализ размерностей стал применяться лишь в 1880-х годах, но это не означает, что раньше никто не оперировал размерностями и не мог умножить людей на (яблоки/человека). В 1880-х пошла тенденция придумывать формулы, опираясь лишь на соображения размерностей, а вписывать правильные размерности в уже готовые формулы умели и раньше.
> очевидное для меня км/ч или л/чел или что угодно еще
> на самом деле даже в конце 19-го века не использовалось
> широко, и всего за последние 100 лет так твердо вошло в
> наш математический язык, что школьники сейчас пользуются
> этим, не задумываясь ни на секунду.
Это утверждение ошибочно. Особенно удивительно, что именно тебе это не очевидно, потому что на нашей-то кафедре анализу размерностей придавали большое значение (хотя вообще-то базовый материал проходили все: он даётся в 11 главе первого тома Сивухина).
Уже сто лет как активно применяется именно метод анализа размерностей: рассматриваются комбинации размерности входных параметров, удовлетворяющие размерности выходного, и размерности анализируются отдельно и до величин. Если говорить о предпосылках развития этого метода, то среди влиятельных работ называют статью Рейнольдса 1883 года. В 1880-90-х годах был ряд работ разных авторов, рассматривавших размерность в отрыве от величин. В 1914 году уже была сформулирована П-теорема, применявшаяся без явной формулировки и раньше.
Таким образом, во-первых, метод размерностей насчитывает уже не 100, а примерно 140 лет.
Если кому-то кажется, что это мало, то вспомните, что 200 лет назад не было уверенности, что вещества состоят из молекул, что тепло - это форма энергии, не было понятия модуля числа, впервые появились химические формулы (в виде трудно читаемых картинок: но ведь и о молекулах тогда консенсуса не было, едва только закон кратных отношений открыли не знали о связи магнетизма и электричества и только-только познакомились с ламарковской концепцией эволюции. Что, это теперь нельзя проходить в школе? Что растениям нужны определённые минеральные вещества, было открыто лишь в 1804 году, причём какие именно — узнали лет 30 спустя. Теперь это проходят в младших классах на уроках природоведения. Фоторецепторы были открыты в 1830-х, а роль колбочек в цветоразличении (о которой догазывались ещё с XIX века) была экспериментально показана лишь в 1950-х годах, что не мешает изучать колбочки на уроках ознакомления с окружающим миром. Да о чём говорить, микробная теория болезней зародилась одновременно с теорией размерностей в начале XIX века и была массово принята в науке тоже одновременно с анализом размерностей: в конце XIX века. Сейчас это рассказывают трёхлетним детям.
И во-вторых. Анализ размерностей стал применяться лишь в 1880-х годах, но это не означает, что раньше никто не оперировал размерностями и не мог умножить людей на (яблоки/человека). В 1880-х пошла тенденция придумывать формулы, опираясь лишь на соображения размерностей, а вписывать правильные размерности в уже готовые формулы умели и раньше.
Во-первых, речь в том посте шла про запись км/ч и л/ч, анализ размерностей упомянут, чтобы было понятно, что к чему. И вовсе не важно 100 или 140 лет назад, пусть хоть 300.
Во-вторых, речь не идет о том, что не надо чему-либо учить. Речь о том, как правильно научить детей умножению, о котором они не имеют никакого представления.
В-третьих, мысль была также о том, что еще рановато обучать ребенка анализу размерностей, когда он еще не может два числа умножить.
Во-вторых, речь не идет о том, что не надо чему-либо учить. Речь о том, как правильно научить детей умножению, о котором они не имеют никакого представления.
В-третьих, мысль была также о том, что еще рановато обучать ребенка анализу размерностей, когда он еще не может два числа умножить.
В-третьих, мысль была также о том, что еще рановато обучать ребенка анализу размерностей, когда он еще не может два числа умножить.+1. Причем хрен пойми какие размерности, которые вводятся в самой задаче неявным образом, в каждой задаче они свои - где яблоки на человека, где человеки на сундук мертвеца. Ненужная методическая каша.
> И вот это меня ошеломило, на самом деле - что стольИ вот вроде хорошо написал, с источниками, датами - а все же двоякое впечатление.
> очевидное для меня км/ч или л/чел или что угодно еще
> на самом деле даже в конце 19-го века не использовалось
> широко, и всего за последние 100 лет так твердо вошло в
> наш математический язык, что школьники сейчас пользуются
> этим, не задумываясь ни на секунду.
Это утверждение ошибочно. Особенно удивительно, что именно тебе это не очевидно, потому что на нашей-то кафедре анализу размерностей придавали большое значение (хотя вообще-то базовый материал проходили все: он даётся в 11 главе первого тома Сивухина).
Уже сто лет как активно применяется именно метод анализа размерностей: рассматриваются комбинации размерности входных параметров, удовлетворяющие размерности выходного, и размерности анализируются отдельно и до величин. Если говорить о предпосылках развития этого метода, то среди влиятельных работ называют статью Рейнольдса 1883 года. В 1880-90-х годах был ряд работ разных авторов, рассматривавших размерность в отрыве от величин. В 1914 году уже была сформулирована П-теорема, применявшаяся без явной формулировки и раньше.
Таким образом, во-первых, метод размерностей насчитывает уже не 100, а примерно 140 лет.
Вот как ты получил 140? 2013 - 1883 = 130. Округлил для значительности? Ай-яй-яй.
И вот почему ты считаешь, что опроверг утверждение "даже в конце 19-го века не использовалось широко", если сам указываешь на пионерские и базовые работы в этой области? Очевидно же, что уровнем ниже, даже в науке, это еще не было стандартом.
Другое дело, что, конечно, в статье перекос, действительно, часть идей, к которым человечество шло мучительно, дальше воспринимались много легче, в том числе и детьми. Это зависит не от того, когда человечество пришло к той или иной идее, а от ее концептуальной сложности - тут ты, имхо, полностью прав.
часть идей, к которым человечество шло мучительно, дальше воспринимались много легче, в том числе и детьми.Детьми воспринимается легко то, что могут правильно объяснить взрослые.
Именно об этом и речь - правильно объяснить умножение. Чтобы дети поняли, когда его надо использовать и как.
Детьми воспринимается легко то, что могут правильно объяснить взрослые.Объясни-ка детям уравнения Максвелла правильно.
Нет, это зависит именно от сложности идеи, микробная теория болезней тут хороший пример.
> Вот как ты получил 140? 2013 - 1883 = 130.
Вычел 1883 из 2023. Фух, слава богу, ошибся
Вычел 1883 из 2023. Фух, слава богу, ошибся
Объясни-ка детям уравнения Максвелла правильно.Сравнение микробной теории болезней с умножением несколько надуманно. То есть их можно сравнивать, если ты хочешь рассказать ребенку, что вот, мол, есть такая штука, как умножение, очень важная и нужная, знай об этом. Ведь на самом деле никакой микробной теории ребенку не рассказывается, а применяется метод микробной страшилки, что дает положительный эффект запоминаемости. Также можно и про уравнения Максвела попугать, что если полезет в розетку, то уравнения Максвела схватят за пальцы и будут больно их трясти. Ребенок скорее всего запомнит и название "уравнения Максвела" и то, что в розетку лучше не лезть. Но как это связано с пониманием умножения, не понятно.
Нет, это зависит именно от сложности идеи, микробная теория болезней тут хороший пример.
Чего ты горбатого лепишь? Дети знают, что такое микроб, более того, у 50% взрослых знания ушли недалеко от этого уровня. Кроме страшилки, есть и идея того, чем вызвано заболевание. С Максвеллом же твоя аналогия не имеет ничего общего с реальностью. Да и в розетке сидит ток, а не уравнения.
Дети знают, что такое микроб, более того, у 50% взрослых знания ушли недалеко от этого уровня. Кроме страшилки, есть и идея того, чем вызвано заболевание. С Максвеллом же твоя аналогия не имеет ничего общего с реальностью. Да и в розетке сидит ток, а не уравнения.Ты сейчас полностью подтвердил мою мысль о том, что и то и другое нельзя сравнивать с умножением.
Mausoleum
Был тут в стади такой хохмопост с фоточкой тетрадки, где в тривиальной задачке (9 покупателям продали по два литра молока; спрашивается, сколько молока продано) решение "9*2=18" зачеркнуто и исправлено на "2*9=18".Меня это дело заинтересовало, я решил проверить - правда ли этой хуйне учат моих детей. Рассмотрел учебники старшего - по счастью, все ок. Подумал, может, фейк, зашел в школьную библиотеку, спросил книжку А.В.Белошистой "Обучение решению задач в начальной школе, книга для учителя". Почитал, охуел.
Скан не мой, из интернетов, с собой фотика не было, но эта страница действительно в наличии, специально проверил:
Путин обыграл меня, сцуко, на моем поле. Неужели единственный выход - учить детей самостоятельно, вне школы?..