Упражнения по математике для школьников
У всех свои вкусы, но если бы я в седьмом классе получил такой листочек по теме "приближенные вычисления" в матлагере, то это был бы мой нелюбимый предмет.
Когда я учился в седьмом классе, я только полюбил математику, у меня появилось представление о доказательствах, об аккуратных рассуждениях. А здесь куча фактов без доказательств, которые непонятно зачем нужны, чтобы приближенно что-то там оценивать. В седьмом классе я бы возмутился и сказал, что к математике это не имеет никакого отношения.
На мой взгляд, это очень неудачный материал для семиклассников и форма его в особенности неудачна. Скажем, на кой хрен им уметь приближенно вычислять биномиальные коэффициенты?
Как минимум, при такой постановке вопроса детей надо было очень сильно заинтересовать этой проблематикой вообще, это дело довольно непростое.
Когда я учился в седьмом классе, я только полюбил математику, у меня появилось представление о доказательствах, об аккуратных рассуждениях. А здесь куча фактов без доказательств, которые непонятно зачем нужны, чтобы приближенно что-то там оценивать. В седьмом классе я бы возмутился и сказал, что к математике это не имеет никакого отношения.
На мой взгляд, это очень неудачный материал для семиклассников и форма его в особенности неудачна. Скажем, на кой хрен им уметь приближенно вычислять биномиальные коэффициенты?
Как минимум, при такой постановке вопроса детей надо было очень сильно заинтересовать этой проблематикой вообще, это дело довольно непростое.
Мне кажется, для седьмого класса это слишком сложно. Нет красочных картинок, один большой текст, а внимание маленького читателя нужно привлекать и максимально экономить.
Думаю, слайды-клипы подошли бы лучше. Типа таких:
Коммутативность сложения:
Коммутативность умножения:

Ассоциативность умножения:
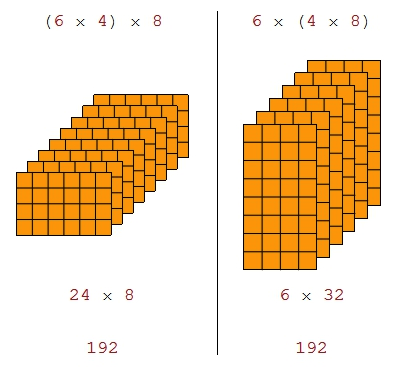
Думаю, слайды-клипы подошли бы лучше. Типа таких:
Коммутативность сложения:

Коммутативность умножения:

Ассоциативность умножения:

Делимость получше, тут достаточно правильный материал. Но общий стиль остается.
Во-первых, фирменная бессвязность. Какая связь первой и второй половин? Только в том, что в конце второй половины появились задачи, связанные с первой. Почему нельзя было не рвать линию, а продолжить вторым семинаром первый - давайте пробовать составлять признаки делимости на 7 в 28ричной системе, это любой сильный школьник придумает сам за 5 минут.
Ну и ростки\плоды - это за гранью, конечно. Я все же надеюсь, что дети этих слов и деления этого не видели.
Во-вторых, фирменная нелюбовь к деталям. Зачем нужно занятие, если его не проработали как следует? Есть отличная тема "Системы счисления", есть классные задачи, где они совершенно нетривиально применяются, скажем, вот А в итоге все осталось на уровне - а вот забавная штука, непонятно на кой хрен она нужна, но поиграем с вами два занятия и разъедемся.
P.S. Задача 8 про Мишу это жесть конечно. Предполагается, что первое действие каждого школьника - вдумчивый анализ того, правда ли у двух и трехзначных чисел буквы "р" и "ш" остаются тогда и только тогда, когда они есть в одной из цифр, входящих в это число? Просто словообразование у нас не совсем прямое, поэтому нужно отследить это на всех конструкциях вида "тринадцать", "сорок один" и т.д
Во-первых, фирменная бессвязность. Какая связь первой и второй половин? Только в том, что в конце второй половины появились задачи, связанные с первой. Почему нельзя было не рвать линию, а продолжить вторым семинаром первый - давайте пробовать составлять признаки делимости на 7 в 28ричной системе, это любой сильный школьник придумает сам за 5 минут.
Ну и ростки\плоды - это за гранью, конечно. Я все же надеюсь, что дети этих слов и деления этого не видели.
Во-вторых, фирменная нелюбовь к деталям. Зачем нужно занятие, если его не проработали как следует? Есть отличная тема "Системы счисления", есть классные задачи, где они совершенно нетривиально применяются, скажем, вот А в итоге все осталось на уровне - а вот забавная штука, непонятно на кой хрен она нужна, но поиграем с вами два занятия и разъедемся.
P.S. Задача 8 про Мишу это жесть конечно. Предполагается, что первое действие каждого школьника - вдумчивый анализ того, правда ли у двух и трехзначных чисел буквы "р" и "ш" остаются тогда и только тогда, когда они есть в одной из цифр, входящих в это число? Просто словообразование у нас не совсем прямое, поэтому нужно отследить это на всех конструкциях вида "тринадцать", "сорок один" и т.д
Между семиклассником и второклассником есть некоторая разница. Алло, в седьмом классе многочлены и параболы проходят в основной программе, а в физматлагерях шпарят комбинаторику и геометрические экстремумы
Алло, в седьмом классе многочлены и параболы проходят в основной программеИ что? Цель матшколы должна быть в углублении знаний, а не в их расширении, тем более сейчас все есть в интернете, нужно только хорошо владеть базовыми понятиями. Думаю, многие семиклассники не знают, как доказать (понять например, ассоциативность умножения, а Иван уже станет рассказывать им про степени.
Цель матшколы должна быть в углублении знаний, а не в их расширении, тем более сейчас все есть в интернете, нужно только хорошо владеть базовыми понятиями
Исходя из позиций "есть в интернете" вообще не нужно никуда ездить, едва ли там будет что-то революционно новое, чего в интернете еще нет.
Углубление и расширение - вообще сложно отличимые понятия в данном случае, так что это игра слов.
Думаю, многие семиклассники не знают, как доказать (понять например, ассоциативность умножения, а Иван уже станет рассказывать им про степени.
Сложный вопрос что вы понимаете под "понять ассоциативность умножения", но неужели вы думаете, что такого рода занятия будут кому-то интересны?
Исходя из позиций "есть в интернете" вообще не нужно никуда ездитьЕздить стоит, чтобы приобрести глубокие базовые понятия в живом общении с умным человеком. Этого ни интернет, ни обычный учитель в школе не дадут.
Сложный вопрос что вы понимаете под "понять ассоциативность умножения"
Что сложного?
Иван, например, говорит 7^6 — это 7*7*7*7*7*7. А школьник Вася спрашивает, что означает эта запись, 7*7)*7)*7)*7) или 7*(7*(7*(7*(7*7 или 7*7)*7)*7*7)*7) или что?
боюсь, что это слишком сложно. мне кажется, надо начать с того, что такое 7 и что такое *. и я думаю, что если я у тебя начну про это серьёзно спрашивать, то ты не сможешь мне объяснить.
Ездить стоит, чтобы приобрести глубокие базовые понятия в живом общении с умным человеком. Этого ни интернет, ни обычный учитель в школе не дадут.
Вам надо переключать режим перед посещение Study. Тут все-таки все более-менее логично и разумно, не Society.
В Сосаити вторым постом опровергнуть свой предыдущий пост вполне типично, а тут как-то ненормально выглядит.
Иван, например, говорит 7^6 — это 7*7*7*7*7*7. А школьник Вася спрашивает, что означает эта запись, 7*7)*7)*7)*7) или 7*(7*(7*(7*(7*7 или 7*7)*7)*7*7)*7) или что?
Вкратце - вы очень плохо думаете о семиклассниках, посещающих физматлагеря.
На таком уровне вопроса не возникнет, а на более глубоком уровне обсуждение ассоциативности (например, для иррациональных чисел) уже довольно специфическое и своеобразное занятие.
Теперь мы знаем, как вывести из себя спокойного Фрау :-)
Хорош грубить-то, нелепо выглишь же.
Если хочешь, чтобы я тебе ответил по существу, сперва остынь и смени тон.
Хорош грубить-то, нелепо выглишь же.
Если хочешь, чтобы я тебе ответил по существу, сперва остынь и смени тон.
Мне кажется, для седьмого класса это слишком сложно. Нет красочных картинок, один большой текст, а внимание маленького читателя нужно привлекать и максимально экономить.как преподававший в том же лагере у 7 же класса скажу, что написана полная чушь. в 7 классе дети гораздо умнее, чем ты о них тут думаешь. У меня решали задачи на проценты, где я вкратце объяснял аннуитетный и дифференцированный платёж по кредиту, комбинаторика вполне себе серьёзная. единственно что они очень плохо допирают до того, что такое индукция. мне как бы сюда выкладывать задачи, которые я давал, лениво, не знаю чем Ваня тут понтануться решил, но про его задачи говорили, что они лёгкие (особенно когда он вполне успешно кое-что из этого давал и 5 классу).
Думаю, слайды-клипы подошли бы лучше. Типа таких:
Коммутативность сложения:
А где я, собственно, грублю? Ты когда писал "буду рад отзывам" имел ввиду, что отзывы должны быть исключительно восторженно положительными?
Ты выложил на критику на свой страх и риск, я почитал и остался совершенно неудовлетворен. Экспертную оценку, я, видимо, могу давать, поскольку из 28 лет жизни 1 год чистого времени я провел в физматлагерях
Вообще выкладывать каждый свой чих на всеобщее осмотрение - довольно некрасивая манера поведения (см. предыдущие выпуски - статью Гонобобеля, методичку Гонобобеля, задачи Гонобобеля но еще и ожидать, что тебе будут при этом кричать "Ай, молодца" - это уж слишком.
Про ответ по существу и вовсе забавно. Правильно я понимаю, что за недостойное мое поведение, ты не ответишь на мою критику твоих семинаров? Mother of God
Ты выложил на критику на свой страх и риск, я почитал и остался совершенно неудовлетворен. Экспертную оценку, я, видимо, могу давать, поскольку из 28 лет жизни 1 год чистого времени я провел в физматлагерях

Вообще выкладывать каждый свой чих на всеобщее осмотрение - довольно некрасивая манера поведения (см. предыдущие выпуски - статью Гонобобеля, методичку Гонобобеля, задачи Гонобобеля но еще и ожидать, что тебе будут при этом кричать "Ай, молодца" - это уж слишком.
Про ответ по существу и вовсе забавно. Правильно я понимаю, что за недостойное мое поведение, ты не ответишь на мою критику твоих семинаров? Mother of God

Мне кажется, идея листочка с приближёнными вычислениями хороша. Конкретная реализация — на вкус и цвет (мне не понравилось, рассчитано на хорошо подготовленных детей, нет ярких, парадоксальных задач). Но сама тема — один из немногих шансов показать, как применяется математика (например, в элементарных оценках из физики или из жизни).
С моей точки зрения рассказ одновременно и о системах счисления, и признаках делимости достаточно сложен. Хотя темы очень тесно связаны между собой, в каждой из них много индивидуальных технических тонкостей, в которых легко запутаться. Если известно, что дети знают обе темы — показать взаимосвязь любопытно, а если нет — боюсь, вреда может оказаться больше, чем пользы. Конкретная реализация меня несколько удивила, непонятно, насколько она удачна, интересно посмотреть на плюсник.
Критические замечания Фрау очень интересны, со многими я согласен.
Не могу не сказать об оформлении листочков. Здорово, что есть некий вступительный текст, какая-то сюжетная линия. (Содержание — другой вопрос, мне нравится далеко не всё.) Мне кажется, заTeXанный листочек всегда красивее вордовского; тем более, был рядом
Кстати, давно собираюсь сделать маленький вики-сайт (даже был, но сгорел где можно было бы организовать свалку разнообразных листочков с комментариями от составителей. Как думаете, это было бы полезно или всем хватает извечных problems.ru / zadachi.mccme.ru / zaba.ru и т.п.?
С моей точки зрения рассказ одновременно и о системах счисления, и признаках делимости достаточно сложен. Хотя темы очень тесно связаны между собой, в каждой из них много индивидуальных технических тонкостей, в которых легко запутаться. Если известно, что дети знают обе темы — показать взаимосвязь любопытно, а если нет — боюсь, вреда может оказаться больше, чем пользы. Конкретная реализация меня несколько удивила, непонятно, насколько она удачна, интересно посмотреть на плюсник.
Критические замечания Фрау очень интересны, со многими я согласен.
Не могу не сказать об оформлении листочков. Здорово, что есть некий вступительный текст, какая-то сюжетная линия. (Содержание — другой вопрос, мне нравится далеко не всё.) Мне кажется, заTeXанный листочек всегда красивее вордовского; тем более, был рядом

Кстати, давно собираюсь сделать маленький вики-сайт (даже был, но сгорел где можно было бы организовать свалку разнообразных листочков с комментариями от составителей. Как думаете, это было бы полезно или всем хватает извечных problems.ru / zadachi.mccme.ru / zaba.ru и т.п.?
Между прочим, если б дело касалось занятия практически без учителя (а не летней матшколы был бы отчасти прав. Однако харизма учителя (Гоно в данном случае) спасает от скукоты.
Ну математику по-разному можно применять.
Тупо оценивать биномиальные коэффициенты без связи хотя бы с какой-нибудь задачей из комбинаторики — вообще странно.
Ладно, короче, вот вершина моей авторской мысли за это лето, чё сам реально придумал на 90% и чё кстати детям жуть как понравилось и в принципе решалось с предварительным объяснением материала, а не то чтобы это были гробы какие-то всё )
http://docs.google.com/file/d/0B506zJlTZCWFYUpKZlgtZGc4NjQ/...
http://docs.google.com/file/d/0B506zJlTZCWFQnJBZm9Ka093QnM/...
Тупо оценивать биномиальные коэффициенты без связи хотя бы с какой-нибудь задачей из комбинаторики — вообще странно.
Ладно, короче, вот вершина моей авторской мысли за это лето, чё сам реально придумал на 90% и чё кстати детям жуть как понравилось и в принципе решалось с предварительным объяснением материала, а не то чтобы это были гробы какие-то всё )
http://docs.google.com/file/d/0B506zJlTZCWFYUpKZlgtZGc4NjQ/...
http://docs.google.com/file/d/0B506zJlTZCWFQnJBZm9Ka093QnM/...
Имхо скучновато в плане уровня задач (но это я по ЛМШ типа Кировской сужу, на месте с конкретными детьми лучше знать вам но в плане подготовки очень круто. Аккуратно, каждая тема хорошо продумана и последовательно изложена, каждая задача проработана, живо и интересно. Респект!
Мне кажется, идея листочка с приближёнными вычислениями хороша. Конкретная реализация — на вкус и цвет (мне не понравилось, рассчитано на хорошо подготовленных детей, нет ярких, парадоксальных задач). Но сама тема — один из немногих шансов показать, как применяется математика (например, в элементарных оценках из физики или из жизни).
Имхо, лучше не 7классникам, а 9-10, когда люди уже задумываются на такие темы и у них в руках уже большой функционал - корни, логарифмы и биномиальные коэффициенты. И тогда сконцентрироваться на том, чтобы реально показать преимущества оценочных , скажем, как проверки вычислений или установления неравенств. Но тогда задачи должны быть специфические, где либо не пробиться (типа больших биномиальных коэффициентов) или где оценки на удивление быстрые. И на одно занятие не стоит и браться, нужно брать серию занятий просто для привития подхода " не тянись за калькулятором". Это да, отличная тема и нас чему-то подобному в школе обучили, я всегда примерно прикидываю правомерность своих вычислений грубыми оценками.
С моей точки зрения рассказ одновременно и о системах счисления, и признаках делимости достаточно сложен. Хотя темы очень тесно связаны между собой, в каждой из них много индивидуальных технических тонкостей, в которых легко запутаться. Если известно, что дети знают обе темы — показать взаимосвязь любопытно, а если нет — боюсь, вреда может оказаться больше, чем пользы. Конкретная реализация меня несколько удивила, непонятно, насколько она удачна, интересно посмотреть на плюсник.
Если посмотреть ссылку на zaba.ru, приведенную выше, то там первые две темы ЛМШ про системы счисления как раз и есть общее понятие и делимость. Просто не надо пытаться объять необъятное - если и 3, и 2, и 5, и 10 и 11 захватить и m^n-1 и системы счисления, то выйдет каша, конечно. А если сразу зайти - а давайте исследовать в m-ричных системах делимость на n, где n делит m, или m-1, то можно прикольную теорию получить, из которой выудить признаки делимости на 9, 3, 5, 2 в 10ричной.
Кстати, давно собираюсь сделать маленький вики-сайт (даже был, но сгорел где можно было бы организовать свалку разнообразных листочков с комментариями от составителей. Как думаете, это было бы полезно или всем хватает извечных problems.ru / zadachi.mccme.ru / zaba.ru и т.п.?
Полезно, если там будет хорошая сортировка, потому что zaba, скажем, практически большая свалка, там хрен найдешь чего надо
где можно было бы организовать свалку разнообразных листочков с комментариями от составителейполезно, т.к. тот же проблемс.ру, с которого для менее занятных тем я тырил постоянно задачи тоже реально уже большая свалка с
а) кучей однотипных задач
б) часто там уже на одну задачу налепят столько тем/тегов, что когда хочешь найти задачи на какую-то тему определённую, прочитаешь ещё гораздо больше, чем нужно.
в) иногда даже составление списка из 10 задач при всё разнообразии становится адом на несколько часов, так как не знаешь из чего выбрать, а так халява )
г) собрать что-то новое и авторское всегда полезно, потому что большинство задач на указанных сайтах относятся к древним баянам и и дети их уже знают, и самого от них тошнит.
Имхо скучновато в плане уровня задач (но это я по ЛМШ типа Кировской сужу, на месте с конкретными детьми лучше знать вам но в плане подготовки очень круто. Аккуратно, каждая тема хорошо продумана и последовательно изложена, каждая задача проработана, живо и интересно. Респект!ну до КЛМШ УЛ как до луны, поэтому по сложности всё ок.
остальные листики всё же были скучнее, но и я как бы не бог преподавания и математической мысли.
ну а так спасибо )
всё-таки раз гоно тут выложил своё творение склёпанное из ворда очень неаккуратно, то я решил показать как оно может быть по-другому
Мне кажется, заTeXанный листочек всегда красивее вордовского; тем более, был рядомЗатеханный листочек - это, конечно, хорошо, но мне одному хочется выколоть себе глаза при виде 7*7*7 и 7^5?
не одному, тем более когда можно легко ставить × и в ворде всё равно писать степени нормально. никакой культуры математической детям не прививается
которые непонятно зачем нужны, чтобы приближенно что-то там оценивать.да ну, семиклассникам понравилось бы
Так нельзя. Для математической школы слишком просто, а для церковно-приходской яблоки не подходят, так как являются символом глехопадения.
Друзья, всем (всем-всем!) спасибо за отзывы. Сейчас нет возможности обстоятельно ответить по существу, напишу позже.
Наконец появилась возможность ответить подробно.
Самое главное: эти листочки - не такие листочки, которые дают детям без комментариев и говорят "решайте, а мы будем проверять". Нет. Сначала преподаватель объясняет теорию у доски, показывает заготовленные (или по ходу придумывает) примеры, решает сам одну-две задачи, отвечает на вопросы. Только потом дети начинают решать сами. Теоретический материал в листочках приведён для справки, на случай, если кто-то что-то не успел переписать с доски.
Без обид, Саша, я уважаю тебя и как человека, и как специалиста, и реально ценю твоё мнение, но, на мой взгляд, такой тон между коллегами недопустим. У каждого свой стиль, и мне нравится твой, с большим удовольствием слушал тебя вместе со студентами. Но это не значит, что твой стиль - единственно правильный. Впрочем, спустя некоторое время я посчитал резкость твоих высказываний за знак доверия... Я был прав?
Листочки техника я сейчас посмотрел. Это совсем другой стиль. Мне он понравился, но он - обычный. И неудивительно, что Фрау, с его многолетним опытом, приходит в восторг. Я не говорю, что мой стиль - лучше; я говорю: мой - более необычный, и потому полезен для детей, так как учиться у разных по подходу учителей очень полезно для разностороннего развития. Материал листочков техника мне понравился, особенно в листке про казино. Подозреваю, что дети решали это с интересом. В листке про финансовую математику имхо можно было бы добавить побольше теории (но это на любителя) для слабоватых детей, которые не знают сложных процентов. Впрочем, я не знаю, что происходило на доске, так что тут не стану критиковать совершенно - не владею основаниями для этого. Там же явно напрашивается приближённое решение показательных уравнений с моего листочка - это позволит ещё больше расширить финансово-математический арсенал детей.
Самое главное: эти листочки - не такие листочки, которые дают детям без комментариев и говорят "решайте, а мы будем проверять". Нет. Сначала преподаватель объясняет теорию у доски, показывает заготовленные (или по ходу придумывает) примеры, решает сам одну-две задачи, отвечает на вопросы. Только потом дети начинают решать сами. Теоретический материал в листочках приведён для справки, на случай, если кто-то что-то не успел переписать с доски.
Скажем, на кой хрен им уметь приближенно вычислять биномиальные коэффициенты?Встречаются в следующей теме про комбинаторику, о чём дети предупреждались. Кроме того, некоторые уже и без нас знали, что такое С.
Как минимум, при такой постановке вопроса детей надо было очень сильно заинтересовать этой проблематикой вообще, это дело довольно непростое.Моим было интересно.
Во-вторых, фирменная нелюбовь к деталям. Зачем нужно занятие, если его не проработали как следует?Ты свечку держал, что ли, чтобы судить о том, что проработали, а что нет? Эти листочки - не на одно занятие; ты об этом не спросил, а сразу начал возмущаться, да ещё и навешивая какие-то ярлыки про "фирменность". Вот именно этот твой апломб я и посчитал хамским и попросил поэтому сменить тон.
Без обид, Саша, я уважаю тебя и как человека, и как специалиста, и реально ценю твоё мнение, но, на мой взгляд, такой тон между коллегами недопустим. У каждого свой стиль, и мне нравится твой, с большим удовольствием слушал тебя вместе со студентами. Но это не значит, что твой стиль - единственно правильный. Впрочем, спустя некоторое время я посчитал резкость твоих высказываний за знак доверия... Я был прав?
не знаю чем Ваня тут понтануться решил, но про его задачи говорили, что они лёгкие (особенно когда он вполне успешно кое-что из этого давал и 5 классу).это было в 3 смене, к 4 смене я усилил листочки. сюда выложил именно усиленную версию. 5 детей из 3 смены пошли в 4-ю опять ко мне, и говорили, что скучно не было, потому что были добавлены новые задачи
Если известно, что дети знают обе темы — показать взаимосвязь любопытно, а если нет — боюсь, вреда может оказаться больше, чем пользы. Конкретная реализация меня несколько удивила, непонятно, насколько она удачна, интересно посмотреть на плюсник.Цель была - объяснить обе темы и показать их взаимосвязь. Материал на несколько занятий. Плюсник попроси у баядерки. Могу и сам дать, если она разрешит.
Вообще выкладывать каждый свой чих на всеобщее осмотрение - довольно некрасивая манера поведения (см. предыдущие выпуски - статью Гонобобеля, методичку Гонобобеля, задачи ГонобобеляНа форуме обосрут, но ведь реально иногда правильные вещи говорят. Качество моих текстов улучшается по итогам обсуждения на форуме. Кому не нравится - пусть не читает. Но каждый раз обычно находится энтузиаст, который не пишет тут громких слов, а сообщает в приват или по почте полезные замечания. А то, что народ обычно сидит сам в своих норах и всего стесняется - это их дело. Я не боюсь выкладывать черновики. Для меня главное - чтобы в итоге получилось хорошо, а не чтобы хвалили. Если бы с подобной резкостью писали слаер или ерсуб, я бы не удивился, но вот именно от не ожидал такого тона.
нет ярких, парадоксальных задачя стараюсь учить тому, чему не учат другие преподаватели, иначе зачем я нужен? все 4 смены я старался учить детей _методам_. яркие идеи встречаются в математических кругах в изобилии, и дети их или уже получили, или ещё получат. а вот методы, подобные тем, которые я излагаю, вряд ли им кто-то покажет.
Листочки техника я сейчас посмотрел. Это совсем другой стиль. Мне он понравился, но он - обычный. И неудивительно, что Фрау, с его многолетним опытом, приходит в восторг. Я не говорю, что мой стиль - лучше; я говорю: мой - более необычный, и потому полезен для детей, так как учиться у разных по подходу учителей очень полезно для разностороннего развития. Материал листочков техника мне понравился, особенно в листке про казино. Подозреваю, что дети решали это с интересом. В листке про финансовую математику имхо можно было бы добавить побольше теории (но это на любителя) для слабоватых детей, которые не знают сложных процентов. Впрочем, я не знаю, что происходило на доске, так что тут не стану критиковать совершенно - не владею основаниями для этого. Там же явно напрашивается приближённое решение показательных уравнений с моего листочка - это позволит ещё больше расширить финансово-математический арсенал детей.
Ну вот, ты опять стал в позу, вместо того, чтобы почитать, что тебе люди пишут.
Есть твои листочки, представляющие занятие. Они сделаны слабо, плохо проработаны темы, поверхностно подобраны задачи, неудачно осуществлены переходы от темы к теме, с плохой мотивировкой, с непонятным принципом подбора материала. Разные люди почитали и более-менее такое мнение о них составили.
Есть листочки техника, они сделаны хорошо, хорошо проработаны, логичны и так далее.
Все выводы основаны на этих листочках и жаловаться, что это мы просто твои занятия не слушали - как минимум глупо. Также как жаловаться на то, что у тебя зато материал крутой, а у техника - нет. Вы выложили конкретные листочки, с конкретным материалом, который каждый из вас решил выбрать. Техник свой материал в листочках проработал качественно, а ты свой - нет.
Не буду отвечать на всю кучу маленьких комментариев, которые ты изложил в своем посту. Замечу только, что ты напрасно думаешь, что необычность сама по себе является чем-то хорошим. Как минимум, чтобы делать что-то новое и необычное, надо сперва досконально разобраться в том, как устроено старое и обычное. Дом с крышей на боку - это необычно, но прежде всего надо, чтобы крыша свои функции продолжила выполнять.
Вспоминая своих любимых учителей в школах, лагерях и университете, могу сказать, что в целом они давали довольно таки обычный материал, просто хорошо проработанный и поданный, что позволяло хорошо и на долгие годы заложить это в голову, четко и упорядоченно.
Есть твои листочки, представляющие занятие. Они сделаны слабо, плохо проработаны темы, поверхностно подобраны задачи, неудачно осуществлены переходы от темы к теме, с плохой мотивировкой, с непонятным принципом подбора материала. Разные люди почитали и более-менее такое мнение о них составили.
Есть листочки техника, они сделаны хорошо, хорошо проработаны, логичны и так далее.
Все выводы основаны на этих листочках и жаловаться, что это мы просто твои занятия не слушали - как минимум глупо. Также как жаловаться на то, что у тебя зато материал крутой, а у техника - нет. Вы выложили конкретные листочки, с конкретным материалом, который каждый из вас решил выбрать. Техник свой материал в листочках проработал качественно, а ты свой - нет.
Не буду отвечать на всю кучу маленьких комментариев, которые ты изложил в своем посту. Замечу только, что ты напрасно думаешь, что необычность сама по себе является чем-то хорошим. Как минимум, чтобы делать что-то новое и необычное, надо сперва досконально разобраться в том, как устроено старое и обычное. Дом с крышей на боку - это необычно, но прежде всего надо, чтобы крыша свои функции продолжила выполнять.
Вспоминая своих любимых учителей в школах, лагерях и университете, могу сказать, что в целом они давали довольно таки обычный материал, просто хорошо проработанный и поданный, что позволяло хорошо и на долгие годы заложить это в голову, четко и упорядоченно.
Во-первых, спасибо за вернувшуюся к тебе вежливость.
Во-вторых, вот это
не факт (как ты это преподносишь а мнение. Мне кажется, оно продиктовано тем, что
Моё преподавательское кредо: ученик - это не мешок, который нужно наполнить, а факел, который нужно зажечь. Человек, представляющий собой горящий факел, сам найдёт нужные ему факты для мешка.
Мои любимые учителя - Абросимов и Смолянов - не всегда и во всём следовали традициям. Смолянов, например, часто ходит на лекции своего спецкурса не готовый вообще. Вообще! Он по ходу дела развивает какую-то мысль, все слушатели участвуют в доказательстве теоремы. При этом он отвлекается на разные замечания и показывает какие-то красивые моменты, которые оказались близки по теме. И сколько бы ни критиковали Смолянова за его стиль, но, тем не менее, Смолянов создал научную школу. А почему? Потому что он рассказывает уникальные вещи, которые больше не рассказывает никто, плюс не боится проявлять свою харизму.
Конечно, мне до Абросимова и Смолянова как пешком до Солнца. Но, тем не менее, мне кажется, что уникальность (на уровне школы) материала моих листочков с лихвой перекрывает те шероховатости, о которых ты пишешь.
В заключение выложу итоговый зачёт. Если ты знаешь, как окончивший 7 класс школьник может решить такие задачи без той теории, которую я предлагал детям, буду рад услышать.
Мне кажется, довольно круто научить детей решать такие задачи. Да, в них нет супер-оригинального взгляда, который отличается от задачи к задаче. Но зато они решаются клёвыми методами, которые взять в свой арсенал полезно, и которым (насколько я знаю) школьников нигде не учат.
Во-вторых, вот это
твои листочки, представляющие занятие. Они сделаны слабо, плохо проработаны темы, поверхностно подобраны задачи, неудачно осуществлены переходы от темы к теме, с плохой мотивировкой, с непонятным принципом подбора материала.
не факт (как ты это преподносишь а мнение. Мне кажется, оно продиктовано тем, что
Вспоминая своих любимых учителей в школах, лагерях и университете, могу сказать, что в целом они давали довольно таки обычный материал, просто хорошо проработанный и поданный, что позволяло хорошо и на долгие годы заложить это в голову, четко и упорядоченно.и поэтому ты перенимаешь манеру этих людей. И ничего плохого в этом я не вижу. Но это не значит, что _все_ преподаватели должны быть именно такими. И что те, которые не такие, слабые или некомпетентные.
Моё преподавательское кредо: ученик - это не мешок, который нужно наполнить, а факел, который нужно зажечь. Человек, представляющий собой горящий факел, сам найдёт нужные ему факты для мешка.
Мои любимые учителя - Абросимов и Смолянов - не всегда и во всём следовали традициям. Смолянов, например, часто ходит на лекции своего спецкурса не готовый вообще. Вообще! Он по ходу дела развивает какую-то мысль, все слушатели участвуют в доказательстве теоремы. При этом он отвлекается на разные замечания и показывает какие-то красивые моменты, которые оказались близки по теме. И сколько бы ни критиковали Смолянова за его стиль, но, тем не менее, Смолянов создал научную школу. А почему? Потому что он рассказывает уникальные вещи, которые больше не рассказывает никто, плюс не боится проявлять свою харизму.
Конечно, мне до Абросимова и Смолянова как пешком до Солнца. Но, тем не менее, мне кажется, что уникальность (на уровне школы) материала моих листочков с лихвой перекрывает те шероховатости, о которых ты пишешь.
В заключение выложу итоговый зачёт. Если ты знаешь, как окончивший 7 класс школьник может решить такие задачи без той теории, которую я предлагал детям, буду рад услышать.
Мне кажется, довольно круто научить детей решать такие задачи. Да, в них нет супер-оригинального взгляда, который отличается от задачи к задаче. Но зато они решаются клёвыми методами, которые взять в свой арсенал полезно, и которым (насколько я знаю) школьников нигде не учат.
асто ходит на лекции своего спецкурса не готовый вообще.сразу понятно, чем это подкупило бездельника гонобобеля

Манеры изложения - это одно, а проработанность листочков - другое. Ты уж определись какой линии ты держишься - что ты неординарный педагог и из этих листочков сделал конфетку или что эти листочки хороши, а я просто предвзят.
В прошлом посте вроде сделан упор на первое, а тут как-то мы вернулись ко второму.
Колмогоров - один из интереснейших людей и сильнейших математиков 20 века, но лектор, афаик, весьма посредственный. Наукой заниматься и увлекать ей людей - это одно, а лекции читать\занятия вести - совсем другое.
Я не знаю, какой ОГ преподаватель, но сомневаюсь, что "не готовиться" - это главная положительная черта его занятий. Уж точно не та, которую тебе следует перенимать
Во-первых, это такая забитая фраза, что ее немного стыдно ставить своим кредо. Все равно что "научить, а не просто рассказать" %)
А во-вторых, на деле кредо никак не подтверждается.
Тебе как раз-таки приводили аргументы, что у тебя плохо выстроены рассуждения, т.е. ты как-то странно зажигаешь факел, а ты в ответ говорил, что у тебя необычный или даже уникальный материал и много интересных методов, т.е. ты хорошо набил мешок.
Разве что эта фраза означает - "неважно, что я написал в листочке, я расскажу это так, что все станут фанатами математики", но тогда надо было видеозапись выкладывать, а не листочек
Вот опять, кредо с факелом, а аргументы о содержании мешка
А надо, чтобы умели решали? А зачем им решать такие задачи они поняли? Прониклись методами или просто научились применять их на пяти типовых задачах? А через полгода если им дать такую задачу на олимпиаде - решат?
Научить решать такие задачи можно, алгоритмы нехитрые. А вот что ты будешь с формулой стирлинга в 7ом классе делать и сколько она у тебя в голове продержится - большой вопрос.
В прошлом посте вроде сделан упор на первое, а тут как-то мы вернулись ко второму.
Смолянов, например, часто ходит на лекции своего спецкурса не готовый вообще. Вообще! ... И сколько бы ни критиковали Смолянова за его стиль, но, тем не менее, Смолянов создал научную школу
Колмогоров - один из интереснейших людей и сильнейших математиков 20 века, но лектор, афаик, весьма посредственный. Наукой заниматься и увлекать ей людей - это одно, а лекции читать\занятия вести - совсем другое.
Я не знаю, какой ОГ преподаватель, но сомневаюсь, что "не готовиться" - это главная положительная черта его занятий. Уж точно не та, которую тебе следует перенимать

Моё преподавательское кредо: ученик - это не мешок, который нужно наполнить, а факел, который нужно зажечь. Человек, представляющий собой горящий факел, сам найдёт нужные ему факты для мешка.
Во-первых, это такая забитая фраза, что ее немного стыдно ставить своим кредо. Все равно что "научить, а не просто рассказать" %)
А во-вторых, на деле кредо никак не подтверждается.
Тебе как раз-таки приводили аргументы, что у тебя плохо выстроены рассуждения, т.е. ты как-то странно зажигаешь факел, а ты в ответ говорил, что у тебя необычный или даже уникальный материал и много интересных методов, т.е. ты хорошо набил мешок.
Разве что эта фраза означает - "неважно, что я написал в листочке, я расскажу это так, что все станут фанатами математики", но тогда надо было видеозапись выкладывать, а не листочек

Если ты знаешь, как окончивший 7 класс школьник может решить такие задачи без той теории, которую я предлагал детям, буду рад услышать
Вот опять, кредо с факелом, а аргументы о содержании мешка

А надо, чтобы умели решали? А зачем им решать такие задачи они поняли? Прониклись методами или просто научились применять их на пяти типовых задачах? А через полгода если им дать такую задачу на олимпиаде - решат?
Научить решать такие задачи можно, алгоритмы нехитрые. А вот что ты будешь с формулой стирлинга в 7ом классе делать и сколько она у тебя в голове продержится - большой вопрос.
И отдельно про задачки, которые научились решать твои дети.
Первый блок задач - 1-3. Задачи некорректно сформулированы, т.к. масштабы погрешности непонятны. То ли у меня спрашивают сколько знаков у полученного числа, то ли сколько знаков у числа знаков.
Дети, по листочку судя, даже примерно не поняли, во сколько раз они при этом ошибаются, тупо научились автозамены делать и руками потом махать.
Таким образом, задачи проверяют научились ли дети подсовывать тебе вместо одного числа другое так, чтобы ты оказался этим удовлетворен. Это довольно бесполезный навык, если они не изберут поприще, связанное с тобой лично.
Второй блок задач - 4-7.
Задачи искусственны и непонятно, где я могу увидеть такую задачу. Таким образом, дети научились решать задачи, которые тебя, боюсь, никто никогда им не даст. Зачем?
Задача 8 тут выглядит вообще непонятно к чему. Для семиклассника задача "может ли сумма двух нечетных чисел быть нечетной" выглядит оскорбительно, честно говоря. В остальном делимость тут рядом не стояло, проверяется знание прямоугольного треугольника с целыми сторонами?
Задача 10. Если они знают индукцию, то задача примитивна. Если не знают (а не должны, вроде) - то сомневаюсь, что ее можно строго обосновать без больших вычислений.
Ну и задача 12. Нужно ли знать оценки из формулы Стирлинга для того, чтобы грубо оценить C^100_50000? Наверное, для столь чудовищно большого числа мне хватит представления о том, сколько же там знаков. Тогда заменю числитель на 50000^{100}, а знаменатель 100! на 50^{100}. Получилось порядка 300 знаков. А точный ответ - 312. Имхо, более чем для любой общежитейской цели
Первый блок задач - 1-3. Задачи некорректно сформулированы, т.к. масштабы погрешности непонятны. То ли у меня спрашивают сколько знаков у полученного числа, то ли сколько знаков у числа знаков.
Дети, по листочку судя, даже примерно не поняли, во сколько раз они при этом ошибаются, тупо научились автозамены делать и руками потом махать.
Таким образом, задачи проверяют научились ли дети подсовывать тебе вместо одного числа другое так, чтобы ты оказался этим удовлетворен. Это довольно бесполезный навык, если они не изберут поприще, связанное с тобой лично.
Второй блок задач - 4-7.
Задачи искусственны и непонятно, где я могу увидеть такую задачу. Таким образом, дети научились решать задачи, которые тебя, боюсь, никто никогда им не даст. Зачем?
Задача 8 тут выглядит вообще непонятно к чему. Для семиклассника задача "может ли сумма двух нечетных чисел быть нечетной" выглядит оскорбительно, честно говоря. В остальном делимость тут рядом не стояло, проверяется знание прямоугольного треугольника с целыми сторонами?
Задача 10. Если они знают индукцию, то задача примитивна. Если не знают (а не должны, вроде) - то сомневаюсь, что ее можно строго обосновать без больших вычислений.
Ну и задача 12. Нужно ли знать оценки из формулы Стирлинга для того, чтобы грубо оценить C^100_50000? Наверное, для столь чудовищно большого числа мне хватит представления о том, сколько же там знаков. Тогда заменю числитель на 50000^{100}, а знаменатель 100! на 50^{100}. Получилось порядка 300 знаков. А точный ответ - 312. Имхо, более чем для любой общежитейской цели
Ты уж определись какой линии ты держишься - что ты неординарный педагог и из этих листочков сделал конфетку или что эти листочки хороши, а я просто предвзят.Моя линия такая: листочки - не конфетка, конечно, но они _свежие_. Именно это и вынесено в заголовок поста. Этим и интересны. Этот материал, насколько я знаю, нигде школьникам не преподавался. Впрочем, возможно, я просто не в курсе. Тут бы как раз и помог твой многолетний опыт знатока того, что обычно рассказывается. Можешь привести места, где рассказывалось всё из моих листочков? Может быть, частично и в разных местах.
Да, на мой взгляд, ты предвзят в плане того, что считаешь, что всё, что не доведено до идеала, должно быть сперва до него доведено, а лишь потом пущено в ход. Ты очень академичен. И это не плохо, просто это такой стиль. Но это не значит, что этот твой стиль - единственно возможный, а остальные - плохи. Если не будет сильных методистов, которые по косточкам разбирают классику, то занятия математикой впоследствии у выпускников превращаются в махание руками, а иногда надо взять и проявить тщательность.
это такая забитая фраза, что ее немного стыдно ставить своим кредона хорошем бояне и сыграть не грех, я считаю. истина не тускнеет от повторения, ну и так далее.
А вот что ты будешь с формулой стирлинга в 7ом классе делать и сколько она у тебя в голове продержится - большой вопрос.упаси ЛММ, формулу Стирлинга я не давал конечно. ты уверен, что смотрел листочек про приближённые вычисления?
С критикой насчёт факела/содержания я согласен. Возможно, тут я сам предвзят в плане того, что меня эти методы зажигают, а кому-то они покажутся наполнением мешка.
Первый блок задач - 1-3. Задачи некорректно сформулированы, т.к. масштабы погрешности непонятны. То ли у меня спрашивают сколько знаков у полученного числа, то ли сколько знаков у числа знаков.слишком академично. иногда требуется получить хоть какое-то приближение, без оценки погрешности. плюс-минус лапоть. чистых математиков от такого выворачивает, но физики пользуются этим постоянно
Дети, по листочку судя, даже примерно не поняли, во сколько раз они при этом ошибаются, тупо научились автозамены делать и руками потом махать.Ирония насчёт поприща засчитана
Таким образом, задачи проверяют научились ли дети подсовывать тебе вместо одного числа другое так, чтобы ты оказался этим удовлетворен. Это довольно бесполезный навык, если они не изберут поприще, связанное с тобой лично.

задача 1 - тут погрешность вычисляется явно, пишется двойное неравенство, как в теории показано. ты точно смотрел листочек?
задача 2 Если ты смотрел листочек, то задачи на приближённое нахождение степеней специально озаглавлены "приближённые вычисления без учёта погрешности". я показывал с помощью ВольфрамАльфа несколько примеров, показывающих, что чем больше знаков у результата, тем больше погрешность. этим решил ограничиться. можно было, кстати, оценить погрешность через приближённое решение показательных уравнений, поскольку ошибка в теоретически данных степенях порядка 2%, что позволит оценить, когда она приведёт к удвоению результата. хорошая идея, спасибо за вдохновение!
задача 3 - то же самое, требуется прикидка. при малых темпах роста/уменьшения (меньше 10%) формула работает хорошо, что бы это ни значило.
Второй блок задач - 4-7.чтобы расширить свой кругозор. признаки делимости в 10-ичной системе входят в стандартную школьную программу, и, на мой взгляд, их легче понять с более высокой точки зрения признаков в m-ичной. потому что сразу становится ясно, что 10, 2 и 5 - просто делители числа 10, 3 и 9 - делители числа 9. а вот 11 - простое, проэтому в 10-ичной оно не порождает кучу признаков, а только один.
Задачи искусственны и непонятно, где я могу увидеть такую задачу. Таким образом, дети научились решать задачи, которые тебя, боюсь, никто никогда им не даст. Зачем?
Задача 8 тут выглядит вообще непонятно к чему. Для семиклассника задача "может ли сумма двух нечетных чисел быть нечетной" выглядит оскорбительно, честно говоря. В остальном делимость тут рядом не стояло, проверяется знание прямоугольного треугольника с целыми сторонами?это простая задача типа утешительного приза. была тема на клетчатую бумагу, задача относится к ней
задача 9 - тоже из темы "чудеса на клетчатой бумаге"
Задача 10. Если они знают индукцию, то задача примитивна. Если не знают (а не должны, вроде) - то сомневаюсь, что ее можно строго обосновать без больших вычислений.на индукцию было занятие, но я отдал изложение теории стажёру и он не идеально справился, да и дети не все были светлы головами, поэтому задача на эту тему такая простая
Ну и задача 12. Нужно ли знать оценки из формулы Стирлинга для того, чтобы грубо оценить C^100_50000? Наверное, для столь чудовищно большого числа мне хватит представления о том, сколько же там знаков. Тогда заменю числитель на 50000^{100}, а знаменатель 100! на 50^{100}. Получилось порядка 300 знаков. А точный ответ - 312. Имхо, более чем для любой общежитейской целиМолодец, хорошее решение
 Я бы делал так же.
Я бы делал так же.Видимо, тут я пересложнил - никто не догадался, что 50000 много больше 100. К сожалению, дети оценивали _каждый_ факториал, в результате вышло много вычислений и никому не хватило времени, чтобы довести их до конца.
А поскольку по расписанию лагеря зачёт проводится в последний день, то провести разбор задач не представляется возможным, поскольку для его качественного проведения надо сначала проверить работы детей, чтобы понять, где были ошибки и на что обратить внимание. К сожалению, я догадался, что надо проводить зачёт в предпоследний день, а в последний - разбор зачёта, только в зачётный день 4-й смены, увы...
Этот материал, насколько я знаю, нигде школьникам не преподавался. Впрочем, возможно, я просто не в курсе. Тут бы как раз и помог твой многолетний опыт знатока того, что обычно рассказывается. Можешь привести места, где рассказывалось всё из моих листочков? Может быть, частично и в разных местах.
Системы счисления, разумеется, преподаются сплошь и рядом, я даже выше ссылку давал.
А аппроксимация в такой форме, разумеется, нет.
Просто потому, что это набор правил, который человека заставляют запомнить совершенно искусственным путем, и он забудет его через неделю. Де факто, ты дал людям на 5 лет раньше в нестрогой форме асимптотические формулы типа первых двух членов бинома ньютона или формулы стирлинга, в которой оставил только логарифмическую асимптотику и е зажал между 2 и 3.
И на что ты при этом рассчитываешь? К математике это не имеет никакого отношения, ты же никаких обоснований дать на их уровне не можешь, это просто некоторое шаманство. Зажечь любовью и интересом это не может.
При этом методы достаточно громоздкие, чтобы без постоянного использования забыть их через неделю, кроме разве что 2^{10} approx 1000 (а это общеизвестный принцип).
Я уже говорил - это очень несвоевременно для 7классника.
Да, на мой взгляд, ты предвзят в плане того, что считаешь, что всё, что не доведено до идеала, должно быть сперва до него доведено, а лишь потом пущено в ход. Ты очень академичен. И это не плохо, просто это такой стиль. Но это не значит, что этот твой стиль - единственно возможный, а остальные - плохи. Если не будет сильных методистов, которые по косточкам разбирают классику, то занятия математикой впоследствии у выпускников превращаются в махание руками, а иногда надо взять и проявить тщательность.
О, я постепенно становлюсь этаким доходягой-методистом, а ты двигателем математики? Ну-ну.

Разговор не об оформлении, не о доводке до идеала, а о выборе материала, подборе задач и т.д. Он крайне неудачен. Есть впечатление, что этот курс сделан так, как тебе хочется его рассказать, а не так, как семиклассникам хотелось бы его послушать. Это плохо, о каком стиле не говори
Итог - ты рассказал им аппроксимацию, делимость, системы счисления, индукцию (? без видимой связи между кусками курса и все достаточно неполно.
Практически ничего из этого они сознательно не смогут применить нигде более, поэтому это забудется без следа неделю спустя.
Хотя выше я выкладывал задачи на системы счисления, которые не напрямую требуют применения этой концепции и помогают взглянуть на них как на полезное подспорье. Если взглянуть на выложенные на забе задачки из вишкильского курса (задачки там частично есть то можно увидеть, что у них по задачам видно логический переход к системам счисления.
Индукции вообще можно хоть целый сезон посвятить, там куча всего интересно.
На делимость пруд пруди замечательных и интересных задач и подходов.
А у тебя всего понемножку, ничего целиком. Именно это я и называю недостаточной проработанностью темы.
В результате возникают штуки как с 12 - ты научил детей слепо пользоваться методом и случайно дал им тривиальную задачу, которую они долбают напролом, потому что используют, но не понимают\не думают.
К слову сказать, весь твой зачет, на мой взгляд, устроен так - используй, но не думай.
Практически ничего из этого они сознательно не смогут применить нигде более, поэтому это забудется без следа неделю спустя.
Хотя выше я выкладывал задачи на системы счисления, которые не напрямую требуют применения этой концепции и помогают взглянуть на них как на полезное подспорье. Если взглянуть на выложенные на забе задачки из вишкильского курса (задачки там частично есть то можно увидеть, что у них по задачам видно логический переход к системам счисления.
Индукции вообще можно хоть целый сезон посвятить, там куча всего интересно.
На делимость пруд пруди замечательных и интересных задач и подходов.
А у тебя всего понемножку, ничего целиком. Именно это я и называю недостаточной проработанностью темы.
В результате возникают штуки как с 12 - ты научил детей слепо пользоваться методом и случайно дал им тривиальную задачу, которую они долбают напролом, потому что используют, но не понимают\не думают.
К слову сказать, весь твой зачет, на мой взгляд, устроен так - используй, но не думай.
И да, я тоже могу провести семинар по специальности экспромтом. Собственно, в разных случаях мне приходится делать это в том или ином виде.
Только к семинару я все равно читаю 5-6 разных книг на эту тему (если столько есть) и сижу и планирую, что же именно тут будет и почему именно такое, а не иное.
Потому что люди долгие годы трудились на этом поприще, писали эти книги и по какой-то причине выстраивали материал в таком порядке. Если я хочу выстроить в другом или взять другую информацию - я должен сперва понять их мотивацию, учесть их идеи.
Почти всегда, когда я выдумываю что-то необычное, выясняется, что это либо неисполнимо, либо при более детальное разработке неудачно. Довольно трудно в популярном направлении придумать что-то принципиально новое.
Только к семинару я все равно читаю 5-6 разных книг на эту тему (если столько есть) и сижу и планирую, что же именно тут будет и почему именно такое, а не иное.
Потому что люди долгие годы трудились на этом поприще, писали эти книги и по какой-то причине выстраивали материал в таком порядке. Если я хочу выстроить в другом или взять другую информацию - я должен сперва понять их мотивацию, учесть их идеи.
Почти всегда, когда я выдумываю что-то необычное, выясняется, что это либо неисполнимо, либо при более детальное разработке неудачно. Довольно трудно в популярном направлении придумать что-то принципиально новое.
Мне не очень хочется вдаваться в детальные обсуждения листочков Гоно (ФрауСоболева сделал это очень подробно). Меня интересует скорее затронутый выше общефилософский вопрос: нужно ли рассказывать нечто принципиально новое или грамотно преподносить старое?
Мне кажется, что однозначного ответа на этот вопрос нет; вся прелесть лагерей подобного Умному лагерю (а изначально Кировской ЛМШ, Новосибирской ЛШ СУНЦ НГУ и т.п.) в том, что школьники видят разных преподавателей. Одни исключительно методично и качественно рассказывают в той или иной степени уже знакомый материал, другие методично и качественно делают некий шажок вперед, третьи рассказывают головокружительные недавние результаты (строгая математическая суть остается за бортом, но остается общее ощущение, как взаимосвязаны разные куски науки четвертые устраивают какие-то игры, пятые, шестые, седьмые делают еще что-то... Преподаватель не доллар, чтобы всем нравится; кому-то понравится первый тип, кому-то второй, кому-то третий...
Разумеется, может быть ситуация, что учитель плохо подготовился к своему занятию (в случае того же Смолянова — не продумал предмет импровизации, или в случае Гоно — сумбурно сделал листки). Из этого не следует, что его методика — катастрофа. Например, на ЛКТГ встречались темы, оформленные с тем же принципом, что и Гоно.
Прелести методичного подхода известны всем; я бы хотел остановиться на нестандартных подходах. Вот, к примеру, выпустил Акопян свою Геометрию в картинках. Никакой особой методики там нет, однако для популяризации эстетики геометрических задач эта книга уже сделала не меньше, чем исключительно продуманный Прасолов. Известная книга Страна математических чудес очень далека от малейшей методики — это некая большая каша занимательного (а то и не очень) добра — но именно подобная книга может убедить читателя в том, что математика не так далеко, как кажется, что книги по математике могут быть красиво оформлены, что там есть место и юмору, и диалогам, и всему.
Работая над Квантиком, я ощутил, насколько важно вдохновлять детей на раздумья о математике. На одной из математических школ я провел для 4-6-классников миникурс по стереометрии (вот черновик конспекта, с ошибками и без картинок). Некоторая необычность темы толкала детей на очень большую свободу действий и мысли, которую я не наблюдал при проведении абсолютно стандартного курса про игры.
Да, придумать что-то новое весьма трудно, я не спорю. Однако даже в случае, когда оно неидеально отшлифовано, это новое может дать весьма благоприятный результат — а может и не дать, так что если есть возможность поэкспериментировать — нужно экспериментировать.
Словом, на ЛМШ листочки всякие нужны, листочки всякие важны, как и мнения по их поводу.
Мне кажется, что однозначного ответа на этот вопрос нет; вся прелесть лагерей подобного Умному лагерю (а изначально Кировской ЛМШ, Новосибирской ЛШ СУНЦ НГУ и т.п.) в том, что школьники видят разных преподавателей. Одни исключительно методично и качественно рассказывают в той или иной степени уже знакомый материал, другие методично и качественно делают некий шажок вперед, третьи рассказывают головокружительные недавние результаты (строгая математическая суть остается за бортом, но остается общее ощущение, как взаимосвязаны разные куски науки четвертые устраивают какие-то игры, пятые, шестые, седьмые делают еще что-то... Преподаватель не доллар, чтобы всем нравится; кому-то понравится первый тип, кому-то второй, кому-то третий...
Разумеется, может быть ситуация, что учитель плохо подготовился к своему занятию (в случае того же Смолянова — не продумал предмет импровизации, или в случае Гоно — сумбурно сделал листки). Из этого не следует, что его методика — катастрофа. Например, на ЛКТГ встречались темы, оформленные с тем же принципом, что и Гоно.
Прелести методичного подхода известны всем; я бы хотел остановиться на нестандартных подходах. Вот, к примеру, выпустил Акопян свою Геометрию в картинках. Никакой особой методики там нет, однако для популяризации эстетики геометрических задач эта книга уже сделала не меньше, чем исключительно продуманный Прасолов. Известная книга Страна математических чудес очень далека от малейшей методики — это некая большая каша занимательного (а то и не очень) добра — но именно подобная книга может убедить читателя в том, что математика не так далеко, как кажется, что книги по математике могут быть красиво оформлены, что там есть место и юмору, и диалогам, и всему.
Работая над Квантиком, я ощутил, насколько важно вдохновлять детей на раздумья о математике. На одной из математических школ я провел для 4-6-классников миникурс по стереометрии (вот черновик конспекта, с ошибками и без картинок). Некоторая необычность темы толкала детей на очень большую свободу действий и мысли, которую я не наблюдал при проведении абсолютно стандартного курса про игры.
Да, придумать что-то новое весьма трудно, я не спорю. Однако даже в случае, когда оно неидеально отшлифовано, это новое может дать весьма благоприятный результат — а может и не дать, так что если есть возможность поэкспериментировать — нужно экспериментировать.
Словом, на ЛМШ листочки всякие нужны, листочки всякие важны, как и мнения по их поводу.
Меня интересует скорее затронутый выше общефилософский вопрос: нужно ли рассказывать нечто принципиально новое или грамотно преподносить старое?
Нужно, конечно. Это прелесть физматлагерей в том, что там рассказывают что-то неожиданное, у нас вон теория групп была в 9 классе в ЛМШ, очень интересно.
К слову о стереометрии, в 8 классе в областном лагере у нас были многогранники, например, обсуждались правильные многогранники и как так получается, что они бывают только такие, какие бывают. Это тоже достаточно наглядно, понятно и интересно.
Только новизна должна быть ориентирована на то, что пригодится\интересно школьнику, а не новизна ради самой новизны. Скажем, в теории групп мы из содержательных фактов доказали только теорему Лагранжа, но весьма содержательно научились применять ее к задачам типа "доказать, что число движений тетраэдра делится на 24". Да и вообще работу со смежными классами хорошо можно использовать в простых задачах.
Я очень хочу на нашем просеминаре по теории вероятностей давать преимущественно новые вещи, но, увы, чтобы до них разумно дойти, приходится повозиться с матожиданиями, дискретными и непрерывными величинами и т.д. Несколько с другой стороны, чем в общем курсе, но все же приходится. Новое должно вложиться в картину мира, а не просто быть каким-то островком в себе.
Тяжело представить себе 7классника, который заинтересуется проблемой аппроксимации биномиальных коэффициентов, только узнав о том, что это такое. Можно его к этому подвести, начав, скажем, со схемы Бернулли, а потом дойдя до задачи типа "какая вероятность, что из 100 000 испытаний будет от 49 500 до 50 500 успехов", но это нужно сделать ведь
Есть, на мой взгляд, некоторые правила преподавания, за которые очень трудно зайти, чтобы получилось что-то хорошее.
Скажем, тема должна вложиться в картину мира человека, должны появиться взаимосвязи с другими, уже известными вещами.
В принципе, необязательно, тема может быть увлекательным миром в себе, но это заметно усложняет задачу - нужно увлечь людей так, чтобы у них вообще не возникло вопроса "А зачем это?"
По возможности должна быть видна логика изложения предмета. Если повествование естественно, то слушателю легче оставаться в предмете, не выключаться. Если оно разрозненно и несвязно, то слушатель выпадает.
Опять же талант преподавателя может компенсировать отсутствие такой логики, можно просто постоянно поддерживать интерес. Но это опять усложняет задачу.
У результатов должен быть показан какой-то интуитивный, содержательный подтекст, тогда слушатели смогут понимать как решать более сложные задачи аналогичным путем.
Опять же это необязательно. Многие любят лекции, где все сухо, подробно, аккуратно и логично. Но это, все-таки, не совсем математика, на мой взгляд.
К слову, знаю, что раз в 3-5 занятий я обязательно проваливаюсь - появляется состояние, в котором я не очень убедителен, интересен, четок. Здесь очень помогает внутренняя логика и проработанность материала, можно выехать на нем даже не в лучшей кондиции. Путь "возьму харизмой", видимо, неизбежно влечет провалы время от времени, когда не сработало
Скажем, тема должна вложиться в картину мира человека, должны появиться взаимосвязи с другими, уже известными вещами.
В принципе, необязательно, тема может быть увлекательным миром в себе, но это заметно усложняет задачу - нужно увлечь людей так, чтобы у них вообще не возникло вопроса "А зачем это?"
По возможности должна быть видна логика изложения предмета. Если повествование естественно, то слушателю легче оставаться в предмете, не выключаться. Если оно разрозненно и несвязно, то слушатель выпадает.
Опять же талант преподавателя может компенсировать отсутствие такой логики, можно просто постоянно поддерживать интерес. Но это опять усложняет задачу.
У результатов должен быть показан какой-то интуитивный, содержательный подтекст, тогда слушатели смогут понимать как решать более сложные задачи аналогичным путем.
Опять же это необязательно. Многие любят лекции, где все сухо, подробно, аккуратно и логично. Но это, все-таки, не совсем математика, на мой взгляд.
К слову, знаю, что раз в 3-5 занятий я обязательно проваливаюсь - появляется состояние, в котором я не очень убедителен, интересен, четок. Здесь очень помогает внутренняя логика и проработанность материала, можно выехать на нем даже не в лучшей кондиции. Путь "возьму харизмой", видимо, неизбежно влечет провалы время от времени, когда не сработало

А это нельзя сделать через парадокс дней рождения? Типа оценить, при скольких людях совпадения начинают случаться часто.
Можно и через него, только возни больше.
Полностью согласен с тем, что в вопросе выбора нового материала нужно иметь вкус и представление об интересах и знаниях школьниках. Однако и тут харизма преподавателя может многое изменить. Так, когда я на 1 курсе слушал лекцию Новикова, то не понял даже темы, на которую она читалась — но меня до глубины души поразило, сколько разных разделов математики было использовано для того, чтобы придумать доказательство (записанное в виде статьи это наверняка была какая-то почти голая теория динамических систем). Так что (в некоторых случаях) нужно рассматривать связку "материал + преподаватель".
Пример с теорией групп хорош. Заинтересоваться аппроксимацией биномиальных коэффициентов можно с помощью известной забавы — доски Гальтона, которую можно несложно сделать вживую.
Про теорию вероятностей, кстати: с 10-классниками мы обсуждали вопрос, сколько ступенек на эскалаторе, если вставал на 140, 200 и 80, а также вот такое:
Подобное задание (с чем-то новым, для чего у них не было соответствующей теории) было на мой взгляд достаточно полезным: кривовато, но они вывели все нужные теории, (с моей помощью) обсудили вероятностные пространства и т.п.
Пример с теорией групп хорош. Заинтересоваться аппроксимацией биномиальных коэффициентов можно с помощью известной забавы — доски Гальтона, которую можно несложно сделать вживую.
Про теорию вероятностей, кстати: с 10-классниками мы обсуждали вопрос, сколько ступенек на эскалаторе, если вставал на 140, 200 и 80, а также вот такое:
Последняя задача на вероятности. Встретилась сегодня в реальной жизни. Покупал кондиционер в Ленте (к слову, еле холодит там акция: за мою покупку дали 10 смурфиков в запечатанных пакетиках. Мне попались вот такие: три с книгой, три кошки, два с гантелями, один бебик и один со сковородкой. Ну а теперь вопрос: на основе этих данных, какая вероятность, что других типов смурфиков нет? Если нужно делать какие-то предположения - делайте на основе здравого смысла. Будем считать что все типы смурфиков распределены одинаково.
Подобное задание (с чем-то новым, для чего у них не было соответствующей теории) было на мой взгляд достаточно полезным: кривовато, но они вывели все нужные теории, (с моей помощью) обсудили вероятностные пространства и т.п.
Системы счисления, разумеется, преподаются сплошь и рядом, я даже выше ссылку давал.насколько я понял, там не формулируются и не доказываются в m-ичной системе счисления признаки делимости на
* степени делителей числа m
* делители числа m-1
* делители числа m+1
а у меня это - главная изюминка, которой я нигде пока не видел. такое ощущение, что ты невнимательно смотрел мои листочки. либо же я что-то не увидел в твоих ссылках, тогда прошу детализировать их.
Зажечь любовью и интересом это не может.ты ж не пробовал такое преподавать, откуда ты знаешь? не слишком ли много уверенности в своей непогрешимости?
О, я постепенно становлюсь этаким доходягой-методистом, а ты двигателем математики? Ну-ну.я бы сказал иначе: ты консерватор, а я - новатор.
опыт развития цивилизации показывает, что для прогресса нужны и те, и другие, и особенно хорошо, если они работают вместе и никто не зазнаётся, объявляя своё мнение истиной в последней инстанции и аргументируя в духе "этого не может быть, потому что этого не может быть никогда". никто не прав полностью, но в творческом взаимодействии мы приближаемся к совершенству ближе, чем в изоляции или борьбе (имхо). потому что не всё новое хорошо (плохо а не всё старое (не) должно быть изменено.
Нужно, конечно. Это прелесть физматлагерей в том, что там рассказывают что-то неожиданное, у нас вон теория групп была в 9 классе в ЛМШ, очень интересно.кстати, знаешь "группу надевания носка"?
Тяжело представить себе 7классника, который заинтересуется проблемой аппроксимации биномиальных коэффициентов, только узнав о том, что это такое. Можно его к этому подвести, начав, скажем, со схемы Бернулли, а потом дойдя до задачи типа "какая вероятность, что из 100 000 испытаний будет от 49 500 до 50 500 успехов", но это нужно сделать ведьтак была же тема "комбинаторика" в курсе. с доказательствами.
насколько я понял, там не формулируются и не доказываются в m-ичной системе счисления признаки делимости на
Т.е. когда тебе показали листочек "Системы счисления - 3", ты не догадался выйти уровнем выше и посмотреть, что же находится в теме "Системы счисления - 2"?

Извини, но если ты не видел нигде признаков делимости на m-1 в m-ричной системе счисления, то ты нигде и не смотрел

Увы, мне остается еще раз повторить - чтобы стать новатором, нужно сперва как следует разобраться в том, кто как и почему делал то, что было до тебя. И с некоторыми общими принципами своего дела разобраться.
А изготовление чего-то кустарными методами без вникания в проблематику и известные в ней результаты - это не новаторство, это то же доказательство теоремы Ферма ручными методами.
Ну всяк на свой уровень примеряет 

у нас вон теория групп была в 9 классе в ЛМШ, очень интересно.да вот только теорию групп тем, кто пойдёт учиться на математика, всё равно расскажут в универе. я же предпочитаю рассказывать то, что не рассказывают в школе, потому что считают, что это слишком сложно (хотя это не так но не рассказывают и в универе, потому что считают, что это слишком просто (хотя это тоже не так).
Т.е. когда тебе показали листочек "Системы счисления - 3", ты не догадался выйти уровнем выше и посмотреть, что же находится в теме "Системы счисления - 2"?да, не догадался
спасибо, что уточнил
 ну что ж, открыл я очередной велосипед, не беда. главное, что дети получили знания.
ну что ж, открыл я очередной велосипед, не беда. главное, что дети получили знания.А изготовление чего-то кустарными методами без вникания в проблематику и известные в ней результаты - это не новаторство, это то же доказательство теоремы Ферма ручными методами.лажи в той теории, которую я предлагал, нет. имхо этого достаточно.
кстати, в плане проработанности имхо мой листочек лучше, чем этот "Системы счисления - 2" http://www.zaba.ru/cgi-bin/tasks.cgi?tour=books.sms701.sspri...
Вань, на забу кто-то выложил задачки с занятий, причем судя по количеству не все. Это не оформленный курс, выложенный на всеобщую критику. Однако по ним видно логику курса, а по твоим, увы, нет.
Заебали. Оба.
а чего бы им сразу метод наименьших квадратов не впарить, у кого менингит случится, запастись таблетками цитрамона и анальгина. А дальше порка мальчиков девочками с розгами и дальше шпарить. Знания ониж ведь только задницей берутся.
дети в этом возрасте должны бегать прыгать общаться играть в казаки разбойники, музыкальный инструмент какой-нибудь освоить, музыка делает взгляд на жизнь абстрактным... научить их играть в шахматы - логика от этого развивается сильно очень.
кстати, не знаю, может подскажете, по физике есть учебник Я.И.Перельмана занимательная физика, для школьников пятиклассников и т.п. А есть ли аналог по математике?
дети в этом возрасте должны бегать прыгать общаться играть в казаки разбойники, музыкальный инструмент какой-нибудь освоить, музыка делает взгляд на жизнь абстрактным... научить их играть в шахматы - логика от этого развивается сильно очень.
кстати, не знаю, может подскажете, по физике есть учебник Я.И.Перельмана занимательная физика, для школьников пятиклассников и т.п. А есть ли аналог по математике?
учебник Я.И.Перельмана занимательная физикаЭто не учебник ни разу (имхо).
Аналоги по математике есть у того же Перельмана; думаю, аналогичнее ЗФ, чем у самого автора ЗФ, не получится ни у кого.
лажи в той теории, которую я предлагал, нет. имхо этого достаточноэх если бы ванятка всегда был такой скромный и трезвый
а то "новаторство" "необычность" "свежесть"

Вань, на забу кто-то выложил задачки с занятий, причем судя по количеству не все. Это не оформленный курс, выложенный на всеобщую критику. Однако по ним видно логику курса, а по твоим, увы, нет.Почему же?
Моя логика: 1. закомимся с системами счисления как таковыми. 2. выводим признаки делимости в системах счисления.
А какая их логика?

tester1
Уважаемые друзья и коллеги,возможно, вас заинтересуют созданные мной этим летом во время преподавания в Умном Лагере учебные материалы. Это - некоторые из листочков, по которым учились "мои" дети. Буду рад отзывам