Зачем нужны тригонометрические формулы
А как бе кто школьникам будет объяснять про комплексные числа?
А если тебя попросят раскрыть cos x+cos y?
плюс еще до кучи, объяснять про комплексную экспоненту и необходимый для нее матанализ.
А если тебя попросят раскрыть cos x+cos y?Что в данном контексте значит слово "раскрыть"? Если требуется, чтобы справа получились x+y. Тогда представляешь x как
А как бе кто школьникам будет объяснять про комплексные числа?А в чем проблема? Серьезно.
думаешь школьникам задают упростить cos^2 (x/2) потому что учителя ответа не знают? 

думаешь школьникам задают упростить cos^2 (x/2) потому что учителя ответа не знают?мне в задачке потребовалось это
Зачем формула эйлера, если все школьные тригонометрические формулы получаются из не менее школьных геометрии и алгебры?
Зачем формула эйлера, если все школьные тригонометрические формулы получаются из не менее школьных геометрии и алгебры?Мне понадобилось упростить вот такое выражение
Будет хорошо, если подход работает для человека, который не сталкивался с этой темой уже 10 лет.
Как бы ты это делал?ну разложил бы косинус двойного угла наоборот. Считать через экспоненты мне бы в голову не пришло

косинус двойного углаЭто надо помнить. Поверь, через 10 лет такие частные случаи выветриваются. А формула Эйлера она проста, поэтому запоминается навсегда. В своё время, когда я познакомился с формулой Эйлера и понял, что все тригонометрические соотношения из нее выводятся тривиально, был приятно обрадован.
Поверь, через 10 лет такие частные случаи выветриваются.не поверю. Через 10 лет после чего? Если голову не использовать, то да, выветриваются. Но не понимаю, как может выветриться это, но не выветриться, как косинус через экспоненту записывается, ну там плюс или минус, есть внизу i или нет. Это все проверяется через элементарные формулы, в голове имеется что-то типа жесткой сети, где все со всем связано и именно поэтому запоминается. Одной формулой все не заменишь.
В своё время, когда я познакомился с формулой Эйлера и понял, что все тригонометрические соотношения из нее выводятся тривиально, был приятно обрадован.Оказалось довольно нетривиальные соотношения между тригонометрическими функциями являются прямыми следствиями простого свойства экспоненты. Это удивительно красивый факт. Почему эту красоту надо скрывать от школьников, а заполнять их мозги уродливыми частными случаями?
А формула Эйлера она проста, поэтому запоминается навсегдада нет, тригонометрические формулы проще запомнить.
Шурик всё верно пишет, из формулы эйлера всё единообразно выводится, а всё множество формул в голове держать это зоология.
ну тут еще вопрос что за школьники. В сунце это все рассказывают. Причем в нашей параллели с комплексным числом мы впервые столкнулись в геометрии, там движение поворот на 90 град. обозначали I, а потом накрутили немного на этом алгебры. Но это не замена тригонометрии, это просто еще один взгляд, который помогает закрепить знания. Например, приведи-ка параллели между формулой эйлера и сферической геометрией. А с обычными были некие параллели. Это все просто идет от узких нужд, тебе одна формула была нужна, вот ты теперь и решил всю тригонометрию выкинуть.
Шурик всё верно пишет, из формулы эйлера всё единообразно выводитсяесли ты не школьник. А школьнику трудно будет выводить, работая с комплексными числами.
Вообще выводить что-то - это всегда слишком сложно для большинства. А запоминать способны более-менее.
Под тригонометрические имелись ввиду тождества. А формула эйлера это как раз экономичная и "правильная" запись двух основных тожество (синус и косинус суммы) из которых всё получается.
если ты не школьник. А школьнику трудно будет выводить, работая с комплексными числами.Вообще выводить что-то - это всегда слишком сложно для большинства. А запоминать способны более-менее.Ну это из разряда, когда оно тебе не нужно, т.е. когда ты школьник, запоминать - это китайская пытка, а когда оно тебе станет нужно для дела, окажется, что есть способ проще и власти скрывали.
ну не знаю, мне например удобнее пользоваться тригонометрией в случаях как у Шурика
ну значит тут речь просто про то, может человек вывести все из базовых формул или нет. А все остальные вспомогательные формулы — это просто "опыт". Т.е. по сути утверждение шурика: "опыт не нужен, я все выведу из базовых формул, причем базовые формулы в форме эйлера я могу запомнить, а в школьной форме — через 10 лет выветрится".
А как бе кто школьникам будет объяснять про комплексные числа?Да, время требуется, но есть и экономия времени. Надо делать оценки того и другого и сравнивать.
Еще встречный вопрос. Зачем школьникам рассказывают алгебру? Рассказывали бы школьникам задачи на «аха» из папируса Ринда и Московского папируса.
Если голову не использовать, то да, выветриваются.А если не касаться 10 лет тригонометрических функций?
Но не понимаю, как может выветриться это, но не выветриться, как косинус через экспоненту записывается, ну там плюс или минус, есть внизу i или нет.
Формула Эйлера выглядит вот так
Это все проверяется через элементарные формулы, в голове имеется что-то типа жесткой сети, где все со всем связано и именно поэтому запоминается.
Расскажи подробнее о своей сети. Очень интересно, как она у тебя устроена.
Как вариант (необязательный можно начать рассказ с упрощения вот этого выражения
Одной формулой все не заменишь.
В этом и есть замечательный факт, что достаточно одной формулы Эйлера и простых свойств экспоненты.
Это все просто идет от узких нужд, тебе одна формула была нужна, вот ты теперь и решил всю тригонометрию выкинуть.
Что значит мне нужна? Мне известен простой способ запоминания, почему его надо скрывать от школьников?
не забывайте, что в школе ввести такую абстракцию как комплексное число — это намного концептуально сложнее, чем пара функций вместо одной. В универе-то сложности наблюдались у некоторых лол 
Сразу становится сложнее с графиками и прочим. Еще не забывайте, что тригонометрия вводится классе в 7м в геометрии, а показательная функция и логарифм попозже.
Т.е. претензия шурика к кому? К тем, кто ему _в школе_ этого не объяснил? Типа всему в школе должны были научить, что ли? На ней образование заканчивается.
Иногда объяснять новые вещи приходится более простым для изначального понимания способом, а не более эффективным на практике. Потому что понимать надо некоторые вещи полностью, а не просто зубрить формулы.

Сразу становится сложнее с графиками и прочим. Еще не забывайте, что тригонометрия вводится классе в 7м в геометрии, а показательная функция и логарифм попозже.
Т.е. претензия шурика к кому? К тем, кто ему _в школе_ этого не объяснил? Типа всему в школе должны были научить, что ли? На ней образование заканчивается.
Иногда объяснять новые вещи приходится более простым для изначального понимания способом, а не более эффективным на практике. Потому что понимать надо некоторые вещи полностью, а не просто зубрить формулы.
ну не знаю, мне например удобнее пользоваться тригонометрией в случаях как у ШурикаОк, допустим это так. Вопрос, какова причина? Тебе это проще, потому что ты прошел муштру школьной программы? Или на то есть объективные причины? Например, меньше требуется запоминать. Можем составить подробные списки для оценки объема информации, которую нужно запоминать в вашем и моем подходе.
Рассказывали бы школьникам задачи на «аха» из папируса Ринда и Московского папируса.
классная ссылка.
Может так и надо, потому что мои нынешние студенты 4-го курса
-не умеют дифференцировать экспоненту: (e^x)'=x*e^x
-не умеют дифференцировать сложную функцию: результат рандомный и непредсказуемый в принципе. Например, "частная производная от f(x-c*t) по x" = f(1)
И это студенты специальностей "теоретическая физика" и "ядерная физика".
Тебе это проще, потому что ты прошел муштру школьной программы?да, именно по этому. Еще я очень благодарен первому семинаристу по матану, который заставил нас вызубрить таблицу элементарных интегралов. Все это сильно ускоряет всякие преобразования, поскольку не требуется тратить время на дополнительные вычисления.
Расскажи подробнее о своей сети. Очень интересно, как она у тебя устроена.я знаю и формулу эйлера и базовые тригонометрические тождества и еще помню всякие факты (например, что sin nx и cos nx выражаются как полином от sin x и cos x). Все это вместе не дает ошибиться, потому что можно проверять результаты разными способами.
Твое выражение упрощается через знание свойства в скобках. Я просто знаю, что все можно свести к функции от половинного угла. Поэтому могу пойти от разложения косинуса в скобках и быть уверенным, что это приведет к результату, а не просто зафигачить формулу эйлера и надеяться, что это даст результат.
(1 - cos x)cos^2 (x/2) = 2sin^2 (x/2) cos^2(x/2) = 1/2 sin^2 x
а не просто зубрить формулы.Писав первый пост я, конечно, не думал так глубоко. Но если задуматься, и посмотреть как сейчас устроено общество, то зазубрив ты можешь пройти искусственный отсев (установленный в обществе) и пробиться к тому, чем тебе интересно будет заниматься. Не зазубришь, не пробьёшься. А потом задним числом ты понимаешь, что зубрешка формул требовалась исключительно для преодоления искусственного отсева, а не для сути того, чем ты хочешь заниматься.
А в чем проблема? Серьезно.проблема, серьезно. В том, что школьники только осваиваются с базовыми понятиями — периодическая функция, обратная функция, производная. Им бы это-то просто понять. А комплексная экспонента заключает все эти свойства в едином (простите) комплексе. Довольно эффективным средством является образное мышление, поэтому и геометрия хорошая наука и графики строят. А построй-ка график e^z. Вот поэтому и начинают более просто.
А то, что есть единый аппарат и единая функция, которая все это в себе содержит, это, конечно, замечательный факт. И люди его знают. Но это не отменяет базовых знаний. И в реальной задаче к ответу ты идешь всеми способами.
Но сводить его к упрощению выражения (1- sin x) cos^2 (x/2) — это просто смешно

Еще я очень благодарен первому семинаристу по матану, который заставил нас вызубрить таблицу элементарных интегралов. Все это сильно ускоряет всякие преобразования, поскольку не требуется тратить время на дополнительные вычисления.Я помню тоже довольно бодро надрачивал на взятие интегралов. А потом в конце обучения познакомился с пакетами Mathematica и Maple и стало как-то неловко, а стоило ли так задрачиваться?
Я помню тоже довольно бодро надрачивал на взятие интегралов. А потом в конце обучения познакомился с пакетами Mathematica и Maple и стало как-то неловко, а стоило ли так задрачиваться?А можно вообще численно считать, ведь так?
Эти пакеты не дают понимания, а только ответ. В реальных задачах часто качественное понимание куда важнее, чем количественный ответ. Поэтому в некоторых областях разрабатываются специальные численные методы, которые дают больше понимания в ущерб общности (http://en.wikipedia.org/wiki/Vortex_lattice_method)
Так и все-таки, раз уж речь зашла о конкретике, выведи формулу cos x + cos y своим методом (сведя к экспоненте). И именно прошу продемонстрировать "запоминание". Т.е. просто подогнать под ответ и я могу. А я потом могу показать, как ее можно вывести/вспомнить помня только формулы двойного угла (они вообще ключевые "подсказки" — узлы моей "сети").
Так и все-таки, раз уж речь зашла о конкретике, выведи формулу cos x + cos y своим методом (сведя к экспоненте). И именно прошу продемонстрировать "запоминание". Т.е. просто подогнать под ответ и я могу.Ключевое я . Могу расписать подробнее, надо?
Получить отсюда выражение для косинуса тривиально.каким образом?
каким образом?вспомнить, что косинус проглатывает минус своего аргумента, а синус выводит минус наружу.
ну т.е. не только формула эйлера, так?
а откуда ты знаешь, что там x+y и x-y? Как это помогает запомнить формула эйлера? Если это туда подставить, то да, очевидно, я об этом написал.
а откуда ты знаешь, что там x+y и x-y?Поэтому я тот пост и начал с вопроса: "Что в данном контексте значит слово "раскрыть"?".
Если брать твою формулировку задачи: "выведи формулу cos x + cos y своим методом ". Она не полна, поскольку формул с указанной левой частью много.
Суть в том, что как только мы знаем, что нам надо найти. Формула Эйлера (+ простые свойства экспоненты и д.р.) дает нам способ получения ответа через механические преобразования.
ну т.е. не только формула эйлера, так?да, свойство экспоненты (я это писал свойства четности косинуса/синуса тоже используются. Полный список я только предлагал выписать. Подозреваю, что мой полный список будет проще вашего.
Как это помогает запомнить формула эйлера?Она не помогает их запомнить. Просто они не нужны, можно всегда пользоваться формулой Эйлера.
А можно вообще численно считать, ведь так?Ой, не скажи. С численными методами куча своих проблем.
В реальных задачах часто качественное понимание куда важнее, чем количественный ответ.
Никто не оспаривает качественного понимания. Оспаривается зубрешка и набивание руки на взятие тех же интегралов.
Например, было бы прикольнее, если бы семинарские и домашние задачки были бы такими, чтобы при их решении можно было бы пользоваться Mathematica. И задачки должны быть такими, чтобы не достаточно было бы применения одной функции Solve. Вот это бы развивало глубокое понимание, действительно.
Например, было бы прикольнее, если бы семинарские и домашние задачки были бы такими, чтобы при их решении можно было бы пользоваться Mathematica. И задачки должны быть такими, чтобы не достаточно было бы применения одной функции Solve. Вот это бы развивало глубокое понимание, действительно.чувак, ты во всех случаях упускаешь одну и ту же мысль: невозможно разобраться глубоко, не поняв основ. И именно так и построено образование. Никто не запрещает тебе пользоваться Mathematica, никто не запрещает в реальной жизни пользоваться лопиталем или эйлером, но заменить ими основы нельзя.
да, свойство экспоненты (я это писал свойства четности косинуса/синуса тоже используются. Полный список я только предлагал выписать. Подозреваю, что мой полный список будет проще вашего.список аксиом на тригонометрические функции вводится на первом курсе, там 5-6 аксиом. То же, что и свойства комплексных чисел+экспонента. Ровно то же, ни больше, ни меньше. Ты отрицаешь просто опыт в тригонометрии.
Школьников уще мучают <бла-бла-бла>?
Есть же mathematica!
Есть же mathematica!
чувак, ты во всех случаях упускаешь одну и ту же мысль: невозможно разобраться глубоко, не поняв основ.где у меня написана мысль, что не надо понимать основы? Запоминание тригонометрических формул это основы? Я утверждаю, можно решать задачи без них.
где у меня написана мысль, что не надо понимать основы? Запоминание тригонометрических формул это основы? Я утверждаю, можно решать задачи без них.ну т.е. ты отрицаешь опыт. Т.е. ты хочешь сказать, что ты можешь решить те же задачи, что и опытный школьник, решивший их 100 и знающий формулы? Готов поспорить, что это не так. Ты вон целый тред раздул из тривиального факта, ладно бы что-нибудь интересное этой формулой показал.
А запомнить аксиоматику что через эйлера, что классическую, труда не составляет.
список аксиом на тригонометрические функции вводится на первом курсе, там 5-6 аксиом. То же, что и свойства комплексных чисел+экспонента. Ровно то же, ни больше, ни меньше.Можешь расписать, какие аксиомы используются при упрощении выражения
Т.е. ты хочешь сказать, что ты можешь решить те же задачи, что и опытный школьник, решивший их 100 и знающий формулы? Готов поспорить, что это не так.Да, могу. Если ты уверен в обратном, тебе, наверное, несложно будет привести один контр пример.
Ты вон целый тред раздул из тривиального факта, ладно бы что-нибудь интересное этой формулой показал.В 21 веке что-то новое из формулы Эйлера?
не новое, а интересное. А ты привел какую-то хуйню тривиальную для седьмого класса и поражаешься.
Школьников уще мучают <бла-бла-бла>?В принципе, да, надо учить с учетом того, что есть Mathematica. По большому счету довольно глупо в 21 веке абстрагироваться от таких пакетов как Mathematica.
Есть же mathematica!
аких пакетов как MathematicaХотя надо признать, интерфейс и язык у этих пакетов очень убог. А это уже следствие того, что нет большого спроса, нет развития. Вон на айфоны Стив сделал спрос, теперь эти отрасли развиваются.
В принципе, да, надо учить с учетом того, что есть Mathematica.Школьников? Ты идиот.
Да, могу.тогда было бы интересно узнать о твоих успехах, к примеру, в математических олимпиадах. Потому что помнится, у меня не только тригонометрические задачи там вызывали трудности.
А контрпример я приводить не обязан, это ты должен доказать свои способности и свою новую мега-теорию.
А про формулу эйлера я тебе так скажу, наоборот часто задачи с комплексными числами решаются через геометрические соображения, где надо как раз от числа переходить к записи через аргумент и модуль, а там как раз классической тригонометрией все делать. Без этого даже не объяснишь суть комплексного умножения. Тут вопрос курицы и яйца, а ты этого видимо не догоняешь совершенно.
Потому что помнится, у меня не только тригонометрические задачи там вызывали трудности.И?
А про формулу эйлера я тебе так скажу, наоборот часто задачи с комплексными числами решаются через геометрические соображения, где надо как раз от числа переходить к записи через аргумент и модуль, а там как раз классической тригонометрией все делать.Как это противоречит том, что я пишу?
ты этого видимо не догоняешь совершенно
Конструктивные аргументы у тебя кончились?
Ты успехи-то перечисли, вот и будет конструктив. Ты же в себе уверен.
Как это противоречит том, что я пишу?ну ты предлагаешь всё выводить из эйлера, значит и синус суммы выводить из эйлера, так?
ты не можешь обсуждать вопрос без выяснения авторитетности?
значит и синус суммы выводить из эйлера, так?Да.
дело не в авторитетности. Ты говоришь, что уверен, что решишь те же задачи, что и опытный школьник (на самом деле у тебя более сильное утверждение, что ты это еще и сделаешь одной формулой эйлера, но не будем этого касаться). Ну вот мне кажется тут хорошей мерой достоверности этого утверждения твои результаты хотя бы на уровне московской олимпиады.
Да.еще: для объяснения эйлера надо объяснить комплексные числа.
А теперь вопрос: как показать геометрический смысл умножения комплексных чисел в этом порядке изложения?
Т.е. что аргумент — это некий угол и что он складывается при умножении. Заметь, сначала числа, потом эйлер, а значит синуса еще нет.
Я довольно поздно плотно познакомился с формулой Эйлера. Но я не хочу сводить разговор к обсуждению меня.
Мне понадобилось упростить вот такое выражение . Как бы ты это делал?
Будет хорошо, если подход работает для человека, который не сталкивался с этой темой уже 10 лет.
Взяла бы вольфрамальфу/python sage и узнала бы всё, что нужно. Подходит даже для тех, кто вообще никогда не сталкивался.
Только причём здесь школа и школьники?
потом эйлер, а значит синуса еще нет.как это формула Эйлера есть, а синуса нет? Синус же входит в формулу Эйлера.
о том и речь 
Синус можно взять как определение из формулы эйлера, это не беда. Беда в том, что у тебя комплексные числа раньше синуса.
Нет, опять, же не беда, можно ввести комплексные числа на матрицах и оттуда плясать.
Еще можно начать с линейных дифуров и показать, откуда эта связь синуса и экспоненты на самом деле растет.
Но это не про школу все.

Синус можно взять как определение из формулы эйлера, это не беда. Беда в том, что у тебя комплексные числа раньше синуса.
Нет, опять, же не беда, можно ввести комплексные числа на матрицах и оттуда плясать.
Еще можно начать с линейных дифуров и показать, откуда эта связь синуса и экспоненты на самом деле растет.
Но это не про школу все.
Со мной была такая история. Я приехал в сунц в 11 класс. И так получилась, что я ничего не знал об экспоненте. Просто даже слова такого не знал. На первой лекции нам сразу дают определение сходимости ряда (формальное через эпсилон). Я приехал из обычной школы. О пределах слухом не слыхивал. Но то определение сходимости и не опиралось на понятие предела. Это было самодостаточное определение сходимости ряда. На той же первой лекции нам выписывают ряд, доказывают его сходимость и обозначают функцией exp(x). Причем именно так через три буквы записывают, и аргумент рядом, а не верхним индексом. Следом за лекцией семинар, где нам даются задачки: самостоятельно доказать, что exp(x+y)=exp(x)exp(y что 2<exp(1)<3 и т.д. Всё это надо сделать из определения через ряд. На одни из выходных я поехал к родителям. Рассказываю маме: “Вот такой замечательный ряд нам рассказали, и название у него такое необычное “экспонента”. Представьте мой шок, когда мама мне отвечает: “Это же е в степени x”. Да, я, наверное, ступил, можно было и самому догадаться из доказанных самостоятельно свойств. Но я даже не задумался об этом в то время. И мне никто не намекнул. Зато с тех пор я понял, что математику можно строить из любой точки. 

Помню в школе мучали запоминанием тригонометрических формул. Косинус суммы и т.п.вот ещё книжка есть по теме http://ilib.mccme.ru/pdf/tr.pdf
запомнить надо косинус и синус суммы, значение синуса и косинуса в нуле и пи пополам, основное тригонометрическое тождество. всё остальное выводится. вывод можно посмотреть в ильине-позняке. там эти равенства принимаются за определение, и из них выводятся все свойства синуса и косинуса
в учебнике Эдмунда Ландау тригонометрические функции вводятся как суммы рядов, и все свойства выводятся из них. тоже подход, но скорее для коллекции.
Зато с тех пор я понял, что математику можно строить из любой точки.но при первом знакомстве лучше выбирать наиболее лёгкий для освоения подход. затем, когда человек уже понял главные свойства объекта, познакомить его с альтернативными определениями и подходами к введению этого объекта. имхо.
запомнить надо косинус и синус суммыФормулу Эйлера проще запомнить. Вы с этим спорите?
но при первом знакомстве лучше выбирать наиболее лёгкий для освоения подход. затем, когда человек уже понял главные свойства объекта, познакомить его с альтернативными определениями и подходами к введению этого объекта. имхо."Наиболее легкий для освоения подход" по мнению преподавателя? А мнение преподавателя формируется той муштрой, через которую его самого пропустили. . Так и получается порочный круг, и никакого развития. В МГУ вроде ученых учат. У ученых должно быть стремление к познанию объективных законов природы.
Во всём-то ты, оказывается, специалист! И как (и какую) науку делать, и как детей учить. Ты просто хрестоматийная иллюстрация эффекта Даннинга — Крюгера.
Во всём-то ты, оказывается, специалист! И как (и какую) науку делать, и как детей учить. Ты просто хрестоматийная иллюстрация эффекта Даннинга — Крюгера.Следующий раз выделяй вот это
За это исследование авторам статьи была присуждена Шнобелевская премия по психологии за 2000 год[4].
Спокойно так выветриваются. Я вот недавно вспоминал формулу для решения квадратных уравнений. Проще вывести, чем вспомнить. Или вот, размышляя о расчёте ценников для нецелого количества литров, решил заменить деление на умножение. Разложил в ряд тейлора только для того, чтобы обнаружить, что получилась геометрическая прогрессия. Простые факты, но не фундаментальные, забываются быстро. Тем более что я никогда их особо не учил, потому что они легко выводимы. Пока пользовался - помнил.
За это исследование авторам статьи была присуждена Шнобелевская премия по психологии за 2000 год[4].Может тебе про Гейма тогда стоит почитать? Хотя, боюсь, ты не поймешь почему.
Может тебе про Гейма тогда стоит почитать? Хотя, боюсь, ты не поймешь почему.Что сказать то хотел? Всё какими-то полунамеками, кроме гнобления собеседника. Это научный стиль общения такой?
Это про то, что шнобелевская премия даётся не за плохие исследования, а за исследования со смешной, часто нелепой формулировкой.
Гейм тоже получал шнобелевскую премию. Не потому, что он днище, а потому что левитирующая лягушка на фоне серьёзной физики вызывает улыбку.
Гейм тоже получал шнобелевскую премию. Не потому, что он днище, а потому что левитирующая лягушка на фоне серьёзной физики вызывает улыбку.
запомнить надо косинус и синус суммынет
Формулу Эйлера проще запомнить. Вы с этим спорите?
Всё какими-то полунамекамиЯ же сказал, что не поймёшь. Видишь ли, мне мой диплом позволяет учить людей с нормальными когнитивными способностями. Дебилов обучают другие люди.
Ты бы не хамил так уж откровенно, в самом деле. Этим ты ничего не добьёшься, а только будешь терять уважение как в глазах оппонента, так и в глазах сторонних наблюдателей.
Определённо, все пишущие в этом треде - не дебилы. И если человек отстаивает (с твоей точки зрения) спорную или маргинальную точку зрения, он от этого дебилом не становится.
Определённо, все пишущие в этом треде - не дебилы. И если человек отстаивает (с твоей точки зрения) спорную или маргинальную точку зрения, он от этого дебилом не становится.
Гейм тоже получал шнобелевскую премию.Про Шнобелевскую премию Гейма я читал.
Это про то, что шнобелевская премия даётся не за плохие исследования, а за исследования со смешной, часто нелепой формулировкой.Спасибо КО. Но опять таки к чему это в этом треде?
...
Не потому, что он днище, а потому что левитирующая лягушка на фоне серьёзной физики вызывает улыбку.
Если ты хочешь оценивать когнитивные способности Шурика, то я рекомендую тебе взять более репрезентативную выборку, чем один тред. А именно, прочие продукты его жизнедеятельности на этом форуме, коих очень много в разделе Development.
Видишь ли, мне мой диплом позволяет учить людей с нормальными когнитивными способностями.Какой у тебя диплом? педагогический?
Еще один гнобер пришел. Что ж вы за мной ходите. Отвалите.
Да не хочу я оценивать когнитивные способности конкретно Шурика. В раздел Девелопмент я не захожу почти. Я хочу попросить вас не ругаться и не называть друг друга дебилами, потому что реальный дебил не поступил бы в МГУ. Побольше уважения к собеседнику и его точке зрения, хотя бы в Стади, было бы не лишним.
Ты бы не хамил так уж откровенно, в самом деле. Этим ты ничего не добьёшься, а только будешь терять уважение как в глазах оппонента, так и в глазах сторонних наблюдателей.Я никогда не хамлю людям, умеющим вести беседу. Сей же персонаж давно и напрочь зарекомендовал себя заносчивым и самовлюбленным дураком. Удивляюсь, что есть ещё люди, пытающиеся с ним вести осмысленную беседу. Полагаю, что либо они очень терпеливые люди, либо просто тренируют искусство риторики.
Да не хочу я оценивать когнитивные способности конкретно Шурика.А я хочу! Чем твои нехотелки лучше моих хотелок?!
Удивляюсь, что есть ещё люди, пытающиеся с ним вести осмысленную беседу. Полагаю, что либо они очень терпеливые люди, либо просто тренируют искусство риторики.просто не читаю треды про SQL

А я хочу! Чем твои нехотелки лучше моих хотелок?!Я просто внёс предложение. Ребят, да делайте что хотите, кто вам может помешать

Сабж (весь тред не читал).
1. Школьный курс алгебры построен так, чтобы всё по возможности доказывалось. Обосновать формулу с комплексной экспонентой непросто — много дополнительных сущностей. А данная с потолка, она вызывает больше вопросов, чем ответов.
2. Пригодились ли лично мне эти полтора десятка формул из школьной тригонометрии? Нет. Я помню только синус и косинус двойного угла, и в университете ни разу от этого не страдал: когда приспичит, можно загуглить или вывести (геомерически или из формулы Эйлера).
3. Стоит ли сократить тригонометрию в школе, направив освободившиеся часы на что-нибудь типа комбинаторики или теорвера? Не знаю. Я бы сократил, но, возможно, я преуменьшаю важность надрачивания на формальные преобразования.
1. Школьный курс алгебры построен так, чтобы всё по возможности доказывалось. Обосновать формулу с комплексной экспонентой непросто — много дополнительных сущностей. А данная с потолка, она вызывает больше вопросов, чем ответов.
2. Пригодились ли лично мне эти полтора десятка формул из школьной тригонометрии? Нет. Я помню только синус и косинус двойного угла, и в университете ни разу от этого не страдал: когда приспичит, можно загуглить или вывести (геомерически или из формулы Эйлера).
3. Стоит ли сократить тригонометрию в школе, направив освободившиеся часы на что-нибудь типа комбинаторики или теорвера? Не знаю. Я бы сократил, но, возможно, я преуменьшаю важность надрачивания на формальные преобразования.
Я просто внёс предложение. Ребят, да делайте что хотите, кто вам может помешать-а я вообще не знаю. Кажется, лишь вчера в Сосите пересекся. Какие у нас педагоги политизированные.

Спасибо КО. Но опять таки к чему это в этом треде?
Ты первым заострил внимание на шнобелевской премии, может быть, объяснишь, зачем?
Ты первым заострил внимание на шнобелевской премии, может быть, объяснишь, зачем?потому что это не серьезно
Что такое "это": исследование, посвящённое эффекту Даннинга — Крюгера, или твой комментарий?
Обосновать формулу с комплексной экспонентой непросто — много дополнительных сущностей.Это не очевидно. Есть доказательство того, что не существует способа ввести комплексные числа без большого количества сущностей?
но, возможно, я преуменьшаю важность надрачивания на формальные преобразования.
нужны более развернутые исследования важности надрачивания
Что такое "это": исследование, посвящённое эффекту Даннинга — Крюгера, или твой комментарий?Шнобелевская премия
Не смейтесь над учёными.
Иногда ученым приходится доказывать научными методами вещи, которые кажутся большинству здравомыслящих людей самоочевидными и не требующими доказательств. Такая необходимость возникает из-за того, что в биологии самоочевидность подчас не является серьезным аргументом. Интуиция и здравый смысл нередко нас подводят (см. главу «Жертвы эволюции», кн. 2). Кроме того, существует особая порода профессоров старшего поколения (особенно много их в психологии, этологии и смежных дисциплинах которые вполне способны отрицать и самоочевидные вещи, если они касаются биологической природы психики и поведения людей. Таких профессоров тоже нужно переубеждать. Поэтому не надо смеяться над учеными, всерьез доказывающими то, что и так «ежу понятно».
Смеяться не надо, но улыбаться не возбраняется. Действительно, трудно сдержать улыбку, когда читаешь научные выводы, подобные опубликованным недавно в уважаемом журнале Behaviour. Группа британских ученых обнародовала факты, позволяющие заключить, что ночные клубы используются (кто бы мог подумать!) как площадки для сексуальных демонстраций (Hendrie et al., 2009):
Молодые, достигшие половой зрелости люди Homo sapiens обоих полов часто собираются в определенных местах и танцуют… Такой тип поведения наблюдается у ряда животных… В настоящем исследовании изучалось это явление в условиях коммерческих ночных клубов. Полученные данные показывают, что более 80 % людей входят в клубы, не имея партнера, и поэтому являются потенциально доступными в сексуальном плане. Наблюдается также примерно 50 %-й рост числа парочек среди выходящих из клуба (по сравнению с входящими что свидетельствует о том, что данные конгрегации образуются с сексуальными целями. Внутри клубов свыше 80 % парных разнополых танцев были инициированы мужчинами, которые подходили к женщинам, а не наоборот. Как следствие, женщины конкурируют друг с другом за привлечение партнеров. Количественная оценка разных женских привлекающих тактик показала, что, хотя лишь 20 % женщин носили тесно облегающую одежду, демонстрирующую более 40 % поверхности их тела или 50 % площади груди и танцевали в сексуальной (sexually suggestive) манере, эти женщины привлекли почти половину (49 %) зарегистрированных нами мужских приглашений на танец. Эти данные указывают на эффективность одежды и танцевальных демонстраций для привлечения мужского внимания и являются веским доводом в пользу того, что ночные клубы представляют собой площадки для сексуальных демонстраций, где женщины соревнуются за мужское внимание. Женщины, осуществляющие наиболее успешные демонстрации, получают преимущество, которое состоит в возможности выбирать из ряда мужчин, проявивших к ним интерес.
запомнить надо косинус и синус суммы, значение синуса и косинуса в нуле и пи пополам, основное тригонометрическое тождество. всё остальное выводится. вывод можно посмотреть в ильине-позняке. там эти равенства принимаются за определение, и из них выводятся все свойства синуса и косинусаВы это что, серьезно, про заучивать?
Синус суммы и теорема Пифагора
Пифагор чуть ли не единственное, что надо помнить для тригонометрии, имхо.
Синус можно взять как определение из формулы эйлера, это не беда. Беда в том, что у тебя комплексные числа раньше синуса.
Обосновать формулу с комплексной экспонентой непросто — много дополнительных сущностей. А данная с потолка, она вызывает больше вопросов, чем ответов.
А всё же давайте попробуем поиграться с введением комплексных чисел.
Вводим комплексные числа просто как пары — стандартная модель (1).
Теперь как бы нам ввести степень с мнимым показателем?
Синус и косинус вводим геометрически, как отношение катетов к гипотенузе, и распространяем на другие значения.
Геометрически доказываем формулы
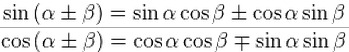 (2)
(2)Теперь обозначим: F(x) = cos(x) + i*sin(x x — вещественное.
Из (1) и (2) доказываем, что
F(x+y) = F(x)*F(y)
F^y(x) = F(x*y)
F(0) = 1
Таким образом, F обладает свойствами показательной функции.
Остается не доказанным, что e это именно 2.71..
Можно ли оставить это школьникам без доказательства? Для манипуляций с e это все равно не используется.
Вы это что, серьезно, про заучивать?А что ты предлагаешь? Заучивать эти геометрические построения по твоей ссылке?
Синус суммы и теорема Пифагора
Не смейтесь над учёными.Проебали вероятно государственные деньги на неважное исследование, это грустно, да.
Синус и косинус вводим геометрически, как отношение катетов к гипотенузе, и распространяем на другие значения.выше ты говорил, что синус суммы вводишь через формулу эйлера.
Геометрически доказываем формулы
выше ты говорил, что синус суммы вводишь через формулу эйлера.Я такого не говорил! Я с самого первого поста утверждаю лишь, что форма в виде формулы Эйлера является самой простой для запоминания и использования в задачках.
Точно, это же ты автор того . Да-да, твои денежки. Корчись.
Нет, их не надо заучивать, они или аналогичные легко придумываются, если школьная геометрия нормально освоена.
Не сложнее, чем решить какую-нибудь легко-олимпиадную геометрическую задачку. Их же решения не заучивают.
Не сложнее, чем решить какую-нибудь легко-олимпиадную геометрическую задачку. Их же решения не заучивают.
По-моему, корчитесь в этом треде вы.  Меня лишь вопросы, связанные с формулой Эйлера, интересуют.
Меня лишь вопросы, связанные с формулой Эйлера, интересуют.
 Меня лишь вопросы, связанные с формулой Эйлера, интересуют.
Меня лишь вопросы, связанные с формулой Эйлера, интересуют.Не сложнее, чем решить какую-нибудь легко-олимпиадную геометрическую задачку. Их же решения не заучивают.Можно пример такой задачи? Сложно представить, чтобы задача была каким-либо образом аналогична ситуации, когда с нуля доказывается фундаментальное свойство.
Я с самого первого поста утверждаю лишь, что форма в виде формулы Эйлера является самой простой для запоминания и использования в задачкахдокажи это утверждение
Проебали вероятно государственные деньги на неважное исследование, это грустно, да.и на твое образование еще проебали. Как думаешь, на что больше?
и на твое образование еще проебали. Как думаешь, на что больше?я сейчас плачу немаленькие налоги, до 650т.р в год — 50%, потом чуть меньше. Т.е. я сейчас треть своего рабочего времени отдаю государству. Этого мало за компенсацию моего образования?
докажи это утверждениеДаже если предположить, что формы формул одинаковы для запоминания, то для суммы косинуса/синуса такая форма:
xxx(a+b)=xxx(a)*xxx(b) +/- xxx(a)*xxx(b)
где xxx это либо косинус, либо синус. Получаем 6 мест, где надо выбирать одно из двух значений. В формуле Эйлера таких мест нет. Все эти места покрываются простым свойством мнимой единицы i.
Получаем 6 месту тебя просто нет "сети" в голове. Еще раз: если помнить про двойной угол, то все сразу становится на свои места
если cos 2x = cos^2 x - sin^2x, то сразу ясно, что cos(a+b) = cos a cos b - sin a sin b аналогично с синусом. Чувак, остановись.
у тебя просто нет "сети" в голове. Еще раз: если помнить про двойной угол, то все сразу становится на свои местаПока то, что ты рассказал про свою "сеть". Это ты дополнительно запоминаешь пару частных случаешь, чтобы не ошибаться при восстановлении по памяти общей формулы. Тест драйвен воспоминания так сказать.
если cos 2x = cos^2 x - sin^2x, то сразу ясно, что cos(a+b) = cos a cos b - sin a sin b аналогично с синусом.
 В случае формулы Эйлера эти усилия не требуются, великие люди уже придали этому более простую форму в виде мнимой единицы i. А ты пользуешься каким-то самосборным велосипедом с квадратными колесами. Но ты молодец в главном — ты об этом говоришь. Другие молчат в тряпочку о своих "сетях", или еще хуже кидаются какашками.
В случае формулы Эйлера эти усилия не требуются, великие люди уже придали этому более простую форму в виде мнимой единицы i. А ты пользуешься каким-то самосборным велосипедом с квадратными колесами. Но ты молодец в главном — ты об этом говоришь. Другие молчат в тряпочку о своих "сетях", или еще хуже кидаются какашками.Это не его "велосипед". Быть может он не очень удачно сформулировал мысль, но многие его поняли. Он говорит про то, что знания не являются набором фактов, которые надо просто запомнить, а образуют систему, между ними есть взаимосвязи. Если ты умеешь видеть эти взаимосвязи - то "запомнить" 6 формул тебе труда составит не больше, чем одну. Просто тебе их и запоминать-то не придется, они сами "возникнут" в голове в нужный момент из этих взаимосвязей. А вот если ты не организовал свои знания в систему - придется зубрить каждую формулу.
Ты в каком-то промежуточном состоянии находишься. Вроде какие-то связи видишь, но зачем они и почему - не понимаешь, и просто считаешь избыточностью.
Эти взаимосвязи, кстати, и есть та причина, почему нужно объяснять тригонометрию через геометрию, а не через комплексные числа. У синуса и косинуса есть вполне наглядная интерпретация, через которую они встраиваются в имеющуюся у школьника на тот момент систему знаний. Комплексную экспоненту там привязать не к чему. Определение ты дашь, но половина класса его забудет едва покинув кабинет математики. Ибо оно осталось висеть в вакууме.
Ты в каком-то промежуточном состоянии находишься. Вроде какие-то связи видишь, но зачем они и почему - не понимаешь, и просто считаешь избыточностью.
Эти взаимосвязи, кстати, и есть та причина, почему нужно объяснять тригонометрию через геометрию, а не через комплексные числа. У синуса и косинуса есть вполне наглядная интерпретация, через которую они встраиваются в имеющуюся у школьника на тот момент систему знаний. Комплексную экспоненту там привязать не к чему. Определение ты дашь, но половина класса его забудет едва покинув кабинет математики. Ибо оно осталось висеть в вакууме.
Так начнем с того, что я вас старше. В вашем положении я был, я помнил все эти формулы. А вот вы в моем положении вы еще не были. Поэтому я могу сравнивать.
Общие слова это, конечно, хорошо. Но у нас есть конкретный пример. Расскажи свою "сеть" на этом конкретном примере. Заодно покажи какие связи не вижу я, и чем это плохо.
Общие слова это, конечно, хорошо. Но у нас есть конкретный пример. Расскажи свою "сеть" на этом конкретном примере. Заодно покажи какие связи не вижу я, и чем это плохо.
Это не его "велосипед". Быть может он не очень удачно сформулировал мысль, но многие его поняли. Он говорит про то, что знания не являются набором фактов, которые надо просто запомнить, а образуют систему, между ними есть взаимосвязи. Если ты умеешь видеть эти взаимосвязи - то "запомнить" 6 формул тебе труда составит не больше, чем одну. Просто тебе их и запоминать-то не придется, они сами "возникнут" в голове в нужный момент из этих взаимосвязей. А вот если ты не организовал свои знания в систему - придется зубрить каждую формулу.Наверное вы относитесь вот к этим парням. Они похожим образом пытаются программировать, . Всё хорошо, но они не могут сказать, когда их процесс создания сети закончится, т.е. когда программа будет работать.

Пока то, что ты рассказал про свою "сеть". Это ты дополнительно запоминаешь пару частных случаешь, чтобы не ошибаться при восстановлении по памяти общей формулы. Тест драйвен воспоминания так сказать.Это просто пример, так устроены все знания, они проверяют друг друга. И формула эйлера тут не отрицается, она дополняет все эти знания.
Например, ты помнишь таблицу умножения? Не выводишь ее вручную из сложения? Или, например, не кажется ли тебе занимательным, что 7*9 = 63 = 8^2 - 1? Зачем запоминать эти произведения нечетных чисел, если все они — разности квадратов? 5 * 9 = 7^2 - 2^2 = 45. Школьников все еще мучают таблицами умножения?
В случае формулы Эйлера эти усилия не требуются, великие люди уже придали этому более простую форму в виде мнимой единицы i.Т.е. ты предлагаешь в уме перемножать многочлены с i? Это как мнемоническое правило куда слабее. Вывести-то можно что угодно, но еще надо как-то удобно запоминать. Вот у тебя выветривается. Может это о чем-то говорит?
Это просто пример, так устроены все знания, они проверяют друг друга.В смысле у формул есть частные случаи? Спасибо, КО.
И формула эйлера тут не отрицается, она дополняет все эти знания.
К тому же она является наиболее компактной формой, в которой содержатся упомянутые частные случаи.
Т.е. ты предлагаешь в уме перемножать многочлены с i?
Кто ж говорит в уме. Механические преобразования делаются на листочке. Сейчас некоторые в компе делают, но я пока по старинке.
Вывести-то можно что угодно, но еще надо как-то удобно запоминать.
Помнить надо только формулу Эйлера.
Вот у тебя выветривается. Может это о чем-то говорит?
Да, выветриваются. И чем это плохо? Да ничем. Моя способность решать задачи нисколько не пострадала. О чем это говорит? О том, что это были лишние узлы сети, время исправило эти излишки.
Примеры с умножением я запомнил в детстве так 7*9=70-7.
Примеры с умножением я запомнил в детстве так 7*9=70-7.да как ты посмел?! все выводится из сложения! 7 * 9 = 9 + 9 + 9 + 9 + 9 + 9 + 9! А число выводится из прибавления единицы!11111
И ты снова не заметил того, о чем я, только самый частный случай. 12*14 = 168 = 13^2 - 1, тоже вот. Я же говорю, гениальная формула, зачем учат таблицам умножения, достаточно помнить квадраты.
В смысле у формул есть частные случаи? Спасибо, КО.это у тебя в голове частный случай, ты только частности и замечаешь. Я тебе еще писал про выражение sin nx через полином, дифуры, собственные числа матрицы, умножение комплексных чисел, геометрию. А у тебя только частный случай...
И так, пошли найзды на мою голову, интерпретируем это, как аргументов больше нет. Поэтому зафиксируем то, что имеем на текущий момент. Для восстановления в памяти косинуса и синуса суммы пользователю требуется помнить:
xxx(a+b)=xxx(a)*xxx(b) +/- xxx(a)*xxx(b)
cos 2x = cos^2 x - sin^2x
sin 2x = 2*cos x * cos x
пользователю требуется
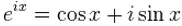
Вывод: пользователю требуется помнить меньше.
xxx(a+b)=xxx(a)*xxx(b) +/- xxx(a)*xxx(b)
cos 2x = cos^2 x - sin^2x
sin 2x = 2*cos x * cos x
пользователю требуется
Вывод: пользователю требуется помнить меньше.
А пользователю и школьникам достаточно помнить теорему Пифагора.
Пример задачки искать не буду, потому что не понимаю — как у конкретного примера сложность оценивать? Зато то, что вступительную стереометрию на мехмат образца 2004 года пользователь не осиливала, на олимпиадах по математике не блистала, а сумму синусов при необходимости выводила геометрически в школе и выводит, если надобится, по сей день — факт.
Если будет предложена какая-нибудь адекватная метрика сложности геометрического вывода, то могу и пример поискать.
Пример задачки искать не буду, потому что не понимаю — как у конкретного примера сложность оценивать? Зато то, что вступительную стереометрию на мехмат образца 2004 года пользователь не осиливала, на олимпиадах по математике не блистала, а сумму синусов при необходимости выводила геометрически в школе и выводит, если надобится, по сей день — факт.
Если будет предложена какая-нибудь адекватная метрика сложности геометрического вывода, то могу и пример поискать.
Вывод: пользователю требуется помнить меньше.мне достаточно помнить единичный круг. Но за счет дополнительных знаний я вспомню и выпишу быстрее, и ошибусь с меньшей вероятностью, а ты плюс на минус где-нибудь в перемножениях многочленов потеряешь и будешь говорить "ну идея-то верная, просто в вычислениях запутался, ща пересчитаю".
sin 2x = 2*cos x * cos xой
 это из формулы эйлера?
это из формулы эйлера? 
Прежде всего давай зафиксируем, что ты отвечаешь на мою цитату про "больше вопросов, чем ответов" применительно к преподаванию в школе.
У вдумчивого мальчика Васи сразу же возникают вопросы:
1) После того, как ты получил, что F(x) обладает свойствами показательной функции, ты вводишь обозначение F(x) = e^{i x}. Заметим, что сейчас ты с таким же успехом можешь положить F(x)=e^x. Но в такой математике возникнет противоречие: e^x + e^{- x} = 2 cos x. Кто обещает, что, подставляя вместо x какие-нибудь комплексные числа, мы не получим противоречия и при _твоём_ подходе?
2) Очевидно тождество e^(2 pi i) = 1. Давай обе части возведём в степень i. Слева будет e^(- 2 pi а справа будет 1^i. 1^i = 1, так как в какую степень единицу ни возводи, она же и получится. Что-то здесь нечисто, да? Как думаешь. сколько времени потребуется на объяснение того, почему на самом деле всё хорошо?
NB. Я критикую не мнимую экспоненту, а конкретно твой подход к её изложению.
У вдумчивого мальчика Васи сразу же возникают вопросы:
1) После того, как ты получил, что F(x) обладает свойствами показательной функции, ты вводишь обозначение F(x) = e^{i x}. Заметим, что сейчас ты с таким же успехом можешь положить F(x)=e^x. Но в такой математике возникнет противоречие: e^x + e^{- x} = 2 cos x. Кто обещает, что, подставляя вместо x какие-нибудь комплексные числа, мы не получим противоречия и при _твоём_ подходе?
2) Очевидно тождество e^(2 pi i) = 1. Давай обе части возведём в степень i. Слева будет e^(- 2 pi а справа будет 1^i. 1^i = 1, так как в какую степень единицу ни возводи, она же и получится. Что-то здесь нечисто, да? Как думаешь. сколько времени потребуется на объяснение того, почему на самом деле всё хорошо?
NB. Я критикую не мнимую экспоненту, а конкретно твой подход к её изложению.
Все эти места покрываются простым свойством мнимой единицы i.у мнимой единицы нужно помнить все арифметические и АЛГЕБРАИЧЕСКИЕ свойства, чтобы с ней нормально работать и не делать ошибок как в примере предыдущего поста.
Или вот пример e^(2*i*pi)=1, так и подмывает взять логарифм и упростить: 2*pi*i=ln(1)=0 - ой, что-то не так, формула Эйлера не работает.
А для алгебраических свойств с i нужен целый курс ТФКП
В общем, спасибо Форточке за удачную мысль. Думаю, наша сторона одерживает победу в этом споре.
У меня написано:
Заметь, я не выписал четвертое свойство показательной функции: a^x*b^x = (a*b)^x. Поскольку не хотел давать определение возведения произвольного действительного числа в комплексную степень. Я даже не доказывал, что e это действительное число. Обозначение F(x)=e^x, это просто обозначение. Считай, что е и ^ это просто символы, как, например, символ F в записи F(x). Т.е. просто сделали замену символов:
F -> e
-> ^
F(x) = cos(x) + i*sin(x x — вещественное.
Заметим, что сейчас ты с таким же успехом можешь положить F(x)=e^x.Не могу, поскольку значение F почти всегда комплексное по определению, см. выше.
Кто обещает, что, подставляя вместо x какие-нибудь комплексные числа, мы не получим противоречия и при _твоём_ подходе?Расширение области определения F на комплексные числа оставляем на потом. Нам это не требуется. Противоречий нет.
2) Очевидно тождество e^(2 pi i) = 1. Давай обе части возведём в степень i. Слева будет e^(- 2 pi а справа будет 1^i. 1^i = 1, так как в какую степень единицу ни возводи, она же и получится. Что-то здесь нечисто, да? Как думаешь. сколько времени потребуется на объяснение того, почему на самом деле всё хорошо?
Заметь, я не выписал четвертое свойство показательной функции: a^x*b^x = (a*b)^x. Поскольку не хотел давать определение возведения произвольного действительного числа в комплексную степень. Я даже не доказывал, что e это действительное число. Обозначение F(x)=e^x, это просто обозначение. Считай, что е и ^ это просто символы, как, например, символ F в записи F(x). Т.е. просто сделали замену символов:
F -> e
-> ^
ой это из формулы эйлера?Это из гугла->из википедии, там картинка, перебивал в ручную, поэтому ошибка. Я и сейчас долго тупил, не замечая два подряд идущих косинуса, чистой воды опечатка. Все опечатки не ловятся проверками, глаз замылмвается. И это факт, об этом в интернете пишут:
По рзелульаттам илссеовадний одонго анлигйсого унвиертисета, не иеемт занчнеия, в кокам пряокде рсапожолена бкувы в солве. Галвоне, чотбы преавя и пслоендяя бквуы блыи на мсете. Осатьлыне бкувы мгоут селдовтаь в плоонм бсепордяке, все-рвано ткест чтаитсея без побрелм. Пичрионй эгото ялвятеся то, что мы не чиатем кдаужю бкуву по отдльенотси, а все солво цликеом.
Так же и мне, верность формулы мне была не критична, мне нужно было просто обозначить ее присутствие.
) Опечатка: не e^x, а e^(ix).
2) Да, так можно выводить формулы тригонометрии. Но причём здесь комплексная экспонента и формула Эйлера? То, что ты сделал на самом деле — всего лишь описал геометрическую интерпретацию комплексных чисел: оператор поворота на угол x то же самое, что умножение на число (cos x + i sin x).
2) Да, так можно выводить формулы тригонометрии. Но причём здесь комплексная экспонента и формула Эйлера? То, что ты сделал на самом деле — всего лишь описал геометрическую интерпретацию комплексных чисел: оператор поворота на угол x то же самое, что умножение на число (cos x + i sin x).
1) Опечатка: не e^x, а e^(ix).
Да, спасибо.
Но причём здесь комплексная экспонента и формула Эйлера?При том, что если в показателе стоит сумма, выражение можно переписать как произведение. Поэтому вводим обозначение близкое к показателю степени. Причем каких-либо пересечений обозначений e^(i*x) и степеней для вещественных чисел, пока не обнаружено, поэтому доказывать пока нечего, вопросов нет.
1) Опечатка: не e^x, а e^(ix).Да. Замена символов такая:
F -> e
-> ^(i*)
Да. Замена символов такая:Сначала ввели некоторый символ i, потом ввели некоторый символ e^(i*). Пока нет пересечений с обозначениями степени вещественных чисел, второе введение символов не хуже первого. А пересечения пока не видно.
F -> e
-> ^(i*)
Так начнем с того, что я вас старше. В вашем положении я был, я помнил все эти формулы. А вот вы в моем положении вы еще не были. Поэтому я могу сравнивать.Эээ... У тебя типа уже старческий склероз наступил?
Общие слова это, конечно, хорошо. Но у нас есть конкретный пример. Расскажи свою "сеть" на этом конкретном примере. Заодно покажи какие связи не вижу я, и чем это плохо.Тебе эти взаимосвязи уже целый тред перечисляют. Ты хочешь чтобы я еще раз все это повторил?
Ну а эффективно это выливается в то, что я эти формулы помню, никаких дополнительных усилий от меня это не требует, и они не выветрились из головы едва я перестал их использовать. А тебе вон приходится "из гугла->из википедии" их перенабивать.
А тебе вон приходится "из гугла->из википедии" их перенабивать.Тебе их не надо перенабивать из своей памяти?
Ты хочешь чтобы я еще раз все это повторил?Да, выпиши.
Пока нет пересечений с обозначениями степени вещественных чисел, второе введение символов не хуже первого.Ну что, товарищи с "сетями", пошукайте там свои сети, есть там такая связь или нет? А я пока попытаюсь найти строгое доказательство, что такой связи нет.
Сначала ввели некоторый символ i, потом ввели некоторый символ e^(i*). Пока нет пересечений с обозначениями степени вещественных чисел, второе введение символов не хуже первого. А пересечения пока не видно.При этом бедные школьники работают с какими-то абстрактными символами, не понимают их сути и зачем всё это нужно
При этом бедные школьники работают с какими-то абстрактными символами, не понимают их сути и зачем всё это нужноА символы бывают не абстрактными?

Для чего понятно, чтобы не запоминать что стоит в местах xxx
xxx(a+b)=xxx(a)*xxx(b) +/- xxx(a)*xxx(b)
Ок, теперь проблема из математической области переходит в педагогическую.
1) Для твоих нужд запись a^x удобнее, чем e^(i x). Буква "а" здесь формальная переменная.
2) Ты предлагаешь использовать нотацию e^(ix при этом оговаривая, что это "специальная" степень, с которой можно делать не всё то же, что и с обычной степенью? Мне кажется, что это не очень эстетично. Какой толк писать букву "e", не рассказывая заговорщицким шёпотом, что это ТО САМОЕ е, и что у комплексной экспоненты есть СМЫСЛ в виде суммы сходящегося ряда? ИМХО.
1) Для твоих нужд запись a^x удобнее, чем e^(i x). Буква "а" здесь формальная переменная.
2) Ты предлагаешь использовать нотацию e^(ix при этом оговаривая, что это "специальная" степень, с которой можно делать не всё то же, что и с обычной степенью? Мне кажется, что это не очень эстетично. Какой толк писать букву "e", не рассказывая заговорщицким шёпотом, что это ТО САМОЕ е, и что у комплексной экспоненты есть СМЫСЛ в виде суммы сходящегося ряда? ИМХО.
А символы бывают не абстрактными?Да, синус и косинус имеют наглядную геометрическую интерпретацию. А твоя F(x) имеет? А комплексные числа как пара вещественных с довольно странным правилом умножения? Я имею в виду такую интерпретацию, которую можно доступно объяснить школьникам.
тред не читал.
мое виденье как проще запоминать(даже скорее выводить) тригонометрические формулы:
достаточно чтобы в голове устаканились следующие тезисы
1) тригонометрическое представление комплексного числа (где стоит косинус а где синус запоминать особо не надо поскольку это прямо следует из определний синуса\косинуса\комплексного числа)
2) при умножении комплексных чисел аргументы складываются(ну в этом факте вроде нет ничего сверхъестесственного)
3а)умножение комплексных чисел(тоже на уровне 5 класса—как умножить a+b на c+d)
3б) i^2=-1
мое виденье как проще запоминать(даже скорее выводить) тригонометрические формулы:
достаточно чтобы в голове устаканились следующие тезисы
1) тригонометрическое представление комплексного числа (где стоит косинус а где синус запоминать особо не надо поскольку это прямо следует из определний синуса\косинуса\комплексного числа)
2) при умножении комплексных чисел аргументы складываются(ну в этом факте вроде нет ничего сверхъестесственного)
3а)умножение комплексных чисел(тоже на уровне 5 класса—как умножить a+b на c+d)
3б) i^2=-1
Тебе их не надо перенабивать из своей памяти?Мне для этого не нужны ни гугл, ни википедия. А вот тебе понадобились.
Да, выпиши.Бесполезная трата времени. Более доступно, чем уже было написано, я объяснить не смогу.
Мне для этого не нужны ни гугл, ни википедия. А вот тебе понадобились.Ты так говоришь, как будто это что-то плохое.
1) Для твоих нужд запись a^x удобнее, чем e^(i x). Буква "а" здесь формальная переменная.Чем удобнее? Количество символов меньше? Этот критерий не всегда учитывается при выборе обозначений. Ты же не предлагаешь обозначать синус s, а косинус c.
2) Ты предлагаешь использовать нотацию e^(ix при этом оговаривая, что это "специальная" степень, с которой можно делать не всё то же, что и с обычной степенью? Мне кажется, что это не очень эстетично. Какой толк писать букву "e", не рассказывая заговорщицким шёпотом, что это ТО САМОЕ е, и что у комплексной экспоненты есть СМЫСЛ в виде суммы сходящегося ряда? ИМХО.
Если в школе проходят ряды, то, конечно, надо рассказать, не вопрос. Если же нет. Я доказал некоторое подмножество A свойств конструкции e^(ix). И предлагаю пользоваться этим подмножеством A. Есть некоторое другое подмножество свойств B. Оно пока не доказано. И пользоваться им пока не стоит. Никто ж не сетовал на то, что как не эстетично устроены числа пока теорема Ферма была не доказана. Наоборот хорошо, это разжигает в школьниках любопытство делать логичные продолжения и искать их доказательства, задавать правильные вопросы.
Да, синус и косинус имеют наглядную геометрическую интерпретацию. А твоя F(x) имеет? А комплексные числа как пара вещественных с довольно странным правилом умножения? Я имею в виду такую интерпретацию, которую можно доступно объяснить школьникам.Ты утверждаешь, что есть геометрическая интерпретация — хорошо, нет — плохо? Это тебе к древним грекам. Они протупили несколько веков, находясь в оковах геометрических трактовок. Наука продолжила развитие после того, как отказались от геометрических трактовок и перешли к абстрактным алгебраическим обозначениям.
Есть некоторое другое подмножество свойств B. Оно пока не доказано. И пользоваться им пока не стоит. Никто ж не сетовал на то, что как не эстетично устроены числа пока теорема Ферма была не доказана. Наоборот хорошо, это разжигает в школьниках любопытство делать логичные продолжения и искать их доказательства, задавать правильные вопросы.Давать школьникам строгую/обоснованную/непротиворечивую, но при этом не закрытую, а открытую систему знаний, имхо, это очень круто. Типа, поплавали тут, посмотрели интересные вещи, и оставили еще, вот туда можно путешествовать.
я говорю о том, что школьникам неинтересно и непонятно будет работать с абстрактными предметами. В науке - да, это необходимо.
я говорю о том, что школьникам неинтересно и непонятно будет работать с абстрактными предметами. В науке - да, это необходимо.Какой смысл ты вкладываешь в слово "абстрактными"? Геометрия сама по себе довольно абстрактная вещь. Это как-то связано с образным мышлением или что?
Давать школьникам строгую/обоснованную/непротиворечивую, но при этом не закрытую, а открытую систему знаний, имхо, это очень круто.в голове у школьников будет каша.
Именно то что школьная математика замкнута со своими косинусами как раз дает шанс школьникам в чем-то разобраться.
в голове у школьников будет каша.такая же как у меня?

А мне ок.
 А у вас попаболь.
А у вас попаболь.Именно то что школьная математика замкнута со своими косинусами как раз дает шанс школьникам в чем-то разобраться.
Обоснуй.
так ты еще не обосновал свое утверждение, а просто ушел от ответа. Ты же выдвинулся первый, тебе первому и доказывать
Но я пойду тебе на встречу и спрошу: какой у тебя опыт в преподавании?
Вот я преподаю с 2005 года, и прекрасно знаю что самое трудное для понимания учащимися - это абстрактные вещи. Я же приводил пример по треду. Что оператор дифференцирования осознается в виде практической таблицы (типа d:sin(x)->cos(x но очень трудно идет в символьном виде (d:f(x)->?). Ты же предлагаешь вводить абстрактные операторы умножения на i, и взятия "типа-экспоненты" e^(i*)
Но я пойду тебе на встречу и спрошу: какой у тебя опыт в преподавании?
Вот я преподаю с 2005 года, и прекрасно знаю что самое трудное для понимания учащимися - это абстрактные вещи. Я же приводил пример по треду. Что оператор дифференцирования осознается в виде практической таблицы (типа d:sin(x)->cos(x но очень трудно идет в символьном виде (d:f(x)->?). Ты же предлагаешь вводить абстрактные операторы умножения на i, и взятия "типа-экспоненты" e^(i*)
Даже вводя абстрактные обозначения, математики НЕ отказывались от геометрических трактовок.
Человеческий мозг так устроен, что лучше всего вычисляет на своей "видеокарте", поэтому геометрическая интерпретация хороша всегда.
Человеческий мозг так устроен, что лучше всего вычисляет на своей "видеокарте", поэтому геометрическая интерпретация хороша всегда.
математики НЕ отказывались от геометрических трактовок
Еще более сложные задачи умели решать с начала II тысячелетия до н.э. в Древнем Вавилоне: в математических текстах, выполненных клинописью на глиняных пластинках, есть квадратные и биквадратные уравнения, системы уравнений с двумя неизвестными и даже простейшие кубические уравнения. При этом вавилоняне также не использовали букв, а приводили решения «типовых» задач, из которых решения аналогичных задач получались заменой числовых данных. В числовой же форме приводились и некоторые правила тождественных преобразований. Если при решении уравнения надо было извлекать квадратный корень из числа , не являющегося точным квадратом, находили приближенное значение корня : делили на и брали среднее арифметическое чисел и .
Первые общие утверждения о тождественных преобразованиях встречаются у древнегреческих математиков, начиная с VI в. до н.э. Среди математиков Древней Греции было принято выражать все алгебраические утверждения в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, произведение двух чисел истолковывали как площадь прямоугольника, а произведение трех чисел – как объем прямоугольного параллелепипеда. Алгебраические формулы принимали вид соотношений между площадями и объемами. Например, говорили, что площадь квадрата, построенного на сумме двух отрезков, равна сумме площадей квадратов, построенных на этих отрезках, увеличенной на удвоенную площадь прямоугольника, построенного на этих отрезках. С того времени и идут термины «квадрат числа» (т.е. произведение величины на самое себя «куб числа», «среднее геометрическое». Геометрическую форму приняло у греков и решение квадратных уравнений – они искали стороны прямоугольника по заданным периметру и площади.
Большинство задач решалось в Древней Греции путем построений циркулем и линейкой (см. Геометрические построения). Но не все задачи поддавались такому решению. Например, «не решались» задачи удвоения куба, трисекции угла, задачи построения правильного семиугольника (см. Классические задачи древности). Они приводили к кубическим уравнениям вида , и соответственно. Для решений этих задач был разработан новый метод, связанный с отысканием точек пересечения конических сечений (эллипса, параболы и гиперболы).
Геометрический подход к алгебраическим проблемам сковывал дальнейшее развитие науки, так как, например, нельзя было складывать величины разных размерностей (длины и площади или площади и объемы нельзя было говорить о произведении более чем трех множителей и т.д. Отказ от геометрической трактовки наметился у Диофанта Александрийского, жившего в III в. В его книге «Арифметика» появляются зачатки буквенной символики и специальные обозначения для степеней неизвестного вплоть до 6-й. Были у него и обозначения для степеней с отрицательными показателями, обозначения для отрицательных чисел, а также знак равенства (особого знака для сложения еще не было краткая запись правил умножения положительных и отрицательных чисел. На дальнейшее развитие алгебры сильное влияние оказали разобранные Диофантом задачи, приводящие к сложным системам алгебраических уравнений, в том числе к системам, где число уравнений было меньше числа неизвестных. Для таких уравнений Диофант искал лишь положительные рациональные решения (см. Диофантовы уравнения).
http://sernam.ru/book_e_math.php?id=5
Greek mathematics got stuck because it remained a verbal, pictorial activity, Moslem "algebra", after a timid attempt at symbolism, died when it returned to the rhetoric style, and the modern civilized world could only emerge —for better or for worse— when Western Europe could free itself from the fetters of medieval scholasticism —a vain attempt at verbal precision!— thanks to the carefully, or at least consciously designed formal symbolisms that we owe to people like Vieta, Descartes, Leibniz, and (later) Boole.
http://www.cs.utexas.edu/users/EWD/transcriptions/EWD06xx/EW...
Таким образом, еще в Вавилоне и Египте появились элементы алгебры, потом тупнят греков в течении нескольких веков. Потом возврат к символьным обозначениям.
Почему греки пошли таким тупиковым путем? Они открыли несоизмеримость отрезков в рациональных числах, поэтому стали не доверять числам и всё делать на геометрических объектах.
Когда возвратились к символьным обозначениям, поняли, что то, что дают символьные преобразования, это круто. А понятие числа надо расширять.

Как бы история нам намекает, замкнутость может завести в тупик.

Как бы история нам намекает, замкнутость может завести в тупик.Еще пример из истории с квантовой механикой. Символьный аппарат для квантовой механики создали, а его строго математического обоснование доказали только спустя несколько десятилетий
http://alexandr4784.narod.ru/rid1/rid1_08_11.pdf
И до сих когда рассказывают квантовую механику не обращают внимание на математическую строгость.
ты не путай науку и учебу
Я вот слежу за данной дискуссией из-за кустов, и горячо поддерживаю сторонников укладки имеющейся информации в сеть понятий из более простых объектов, уже известных и хорошо осознаваемых школьниками. И формальная якобы простота запоминания одной, а не нескольких формул, здесь гарантированно мнимая. Так как у того же Шурика формула Эйлера как основание для вычисления соотношений синусов и косинусов осозналась уже пост фактум, после того, как он более-менее разобрался с экспонентой и экспонента сама образовала свою минисеть понятий в мозгу, в контекст которых синус с косинусом и легли. Но в силу случайности эта оказалась устойчивей, чем та, о которой говорит пользователь ункулункулункулу. А у большинства школьников этого не произойдёт именно потому, что это очень абстрактное понятие, которое останется в мозгу олгое время изолированным, а для большинства - изолированным навсегда. И это значит, что большинство его быстро не вспомнит, в отличие от более привычных геометрических зацепок. Физиологически вероятность попасть сигналу электрическому из области А в область Б тем выше (лёгкость вспомнить чем больше путей ведут из области А в область Б. И путь сторонников геометрического подхода педагогически и физиологически более оправданный. И формальное количество формул на запоминание здесь не имеет никакого значения - сложно вспоминается не количество, а более изолированное, чем менее изолированное понятие. А формула Эйлера и экспонента для 7-8-классника окажется гарантированно ОЧЕНЬ изолированным понятием, кодируемым клеточным ансамблем нейроном, не имеющим большого количества устойчивых связей сдругиим ансамблями мозга. Поэтому и вспоминаться, и использоваться (т.е. строить новые связи с другими элементами) у большинства школьников он будет с проблемами. И формальное количество элементов для запоминания не будет иметь в данном случае никакого значения.
У тех, кто успешно занимается наукой или в общем случае решением задач, основополагающим является как навык поиска связей между новым явлением и тем, что уже есть в голове, так и формирование этих связей с нуля на основе условных правил с помощью правил логики и т.д. Но большинство школьников последнему навыку нужно учить специально.
У тех, кто успешно занимается наукой или в общем случае решением задач, основополагающим является как навык поиска связей между новым явлением и тем, что уже есть в голове, так и формирование этих связей с нуля на основе условных правил с помощью правил логики и т.д. Но большинство школьников последнему навыку нужно учить специально.
А где тут наука и где учеба?
Пока новое это наука, потом превращается у учебу.
Пока новое это наука, потом превращается у учебу.
Пока новое это наука, потом превращается у учебу.однако учат чему-то совсем не так как до этого в свое время додумывались
вот, т.е. в некотором смысле можно сказать, что запомнить больше может быть проще, чем запомнить меньше  всегда это чувствовал
всегда это чувствовал 
 всегда это чувствовал
всегда это чувствовал 
уже известных и хорошо осознаваемых школьникамит.е. подход, который не обучает новому
Я вот слежу за данной дискуссией из-за кустов, и горячо поддерживаю сторонников укладки имеющейся информации в сеть понятий из более простых объектов, уже известных и хорошо осознаваемых школьниками. И формальная якобы простота запоминания одной, а не нескольких формул, здесь гарантированно мнимая. Так как у того же Шурика формула Эйлера как основание для вычисления соотношений синусов и косинусов осозналась уже пост фактум, после того, как он более-менее разобрался с экспонентой и экспонента сама образовала свою минисеть понятий в мозгу, в контекст которых синус с косинусом и легли. Но в силу случайности эта оказалась устойчивей, чем та, о которой говорит пользователь ункулункулункулу. А у большинства школьников этого не произойдёт именно потому, что это очень абстрактное понятие, которое останется в мозгу олгое время изолированным, а для большинства - изолированным навсегда. И это значит, что большинство его быстро не вспомнит, в отличие от более привычных геометрических зацепок. Физиологически вероятность попасть сигналу электрическому из области А в область Б тем выше (лёгкость вспомнить чем больше путей ведут из области А в область Б. И путь сторонников геометрического подхода педагогически и физиологически более оправданный. И формальное количество формул на запоминание здесь не имеет никакого значения - сложно вспоминается не количество, а более изолированное, чем менее изолированное понятие. А формула Эйлера и экспонента для 7-8-классника окажется гарантированно ОЧЕНЬ изолированным понятием, кодируемым клеточным ансамблем нейроном, не имеющим большого количества устойчивых связей сдругиим ансамблями мозга. Поэтому и вспоминаться, и использоваться (т.е. строить новые связи с другими элементами) у большинства школьников он будет с проблемами. И формальное количество элементов для запоминания не будет иметь в данном случае никакого значенияЭто повествование самоприменимо. То, чего нет в "сетевом" мозгу им не воспримется, точнее воспринимается с большим трудом. "Несетевому" мозгу такое повествование очень сложно читать, поскольку после каждого предложения вопросы: а это откуда? а это зачем? а это почему? "Сетевой" же мозг спокойно образовывает свою сеть, и не важно какую чушь в нее записывают, главное, чтобы связей было побольше.
А суть в том, что о человеческом мозге сейчас никто не знает. Поэтому логичнее пользоваться тем, что известно о реальных людях, о том что происходило в истории. А не строить высосанные из пальца и не имеющие никакого отношения к реальному мозгу человека модели.
Я не вижу ни одного примера отказа от геометрической интерпретации. Числа и по сей день можно представлять как длину отрезка или площадь квадрата.
В квантовой механике я также не вижу геометрическую интерпретацию, от которой был бы отказ. Более того, я сдавал спецкурс "геометрические методы квантовой механики".
В математике вообще чем больше способов взглянуть на вещь — тем лучше.
В квантовой механике я также не вижу геометрическую интерпретацию, от которой был бы отказ. Более того, я сдавал спецкурс "геометрические методы квантовой механики".
В математике вообще чем больше способов взглянуть на вещь — тем лучше.
"Сетевой" же мозг спокойно образовывает свою сеть, и не важно какую чушь в нее записывают, главное, чтобы связей было побольше.И да, и нет.
Сетевой мозг как концепция в настоящее время никем особо не оспаривается - есть множество фактов, которые им отлично объясняются.. И в свою очередь существует тонкая грань между мозгом параноика и нормального человека. У параноика он работает именно так, как ты сказал - он любую чушь укладывает в систему. Я тебе больше скажу - наш мозг физиологически заточен под то, чтобы из фактов строить систему. Именно из-за этого так живучи приметы (поиск закономерностей на основе случайно совпавших действий - мозг их отлично запоминает, фильтрует и цепляет новые факты на них - анекдот про слоновьи яйца! и считается,что именно это является основанием наличия религии. А дальше идёт баланс между лёгкостью\ сложностью верификации старых связей новой информацией и лёгкостью\сложностью перестройки связей на основании новой системы или подчинения старой системой новой информации. Качнуть в строну тяжёлой перестройки -получишь консерватора, с трудом усваивающего новое, не могущего взглянуть на явление под новым углом и плохо обучаемого. Качнуть в сторону лёгкости перестройки-получишь скорее всего вообще неадекватно работающий мозг или мозг психически ненормального человека.
Я не вижу ни одного примера отказа от геометрической интерпретации. Числа и по сей день можно представлять как длину отрезка или площадь квадрата.Это сейчас можно. А древним грекам нельзя было.
Числа у них были только рациональные. Буквы, обозначали именно рациональные числа. После открытия теоремы Пифагора они с ужасом осознали, что отрезки несоизмеримы в рациональных числах. Т.е. они построили два отрезка, которые не относятся как два числа. Это было очень печальное известие. Они подзабили на числа и, соответственно, на алгебру и стали всё решать и доказывать через геометрические построения.
В квантовой механике я также не вижу геометрическую интерпретацию, от которой был бы отказ. Более того, я сдавал спецкурс "геометрические методы квантовой механики".
Сейчас лейбл "геометрический" к чему только не приклеивают, но от такой геометричности обывателю или школьнику легче не станет. ОТО тоже геометрическая.

если тебе для упрощения твоего примера нужна формула Эйлера, ты феерический дебил
(1 - cos x) cos^2 x/2 = (1 - cos (2x)/2) cos^2 x/2,
дальше x/2 = t
(1 - cos 2t) cos^2 t = (1 - 1 + 2 sin^2 t) cos^2 t = 2 sin^2 t cos^2 t = sin^2 x / 2
(1 - cos x) cos^2 x/2 = (1 - cos (2x)/2) cos^2 x/2,
дальше x/2 = t
(1 - cos 2t) cos^2 t = (1 - 1 + 2 sin^2 t) cos^2 t = 2 sin^2 t cos^2 t = sin^2 x / 2
Качнуть в сторону лёгкости перестройки-получишь скорее всего вообще неадекватно работающий мозг или мозг психически ненормального человека.А это никак не связано с повышенным количеством ненормальных среди лиц определённых родов занятий?
т.е. подход, который не обучает новомуЭто подход, которые максимально облегчает построение мозгом школьника цельной связной математической системы, который обучает его выводить из одних свойств другие, не обедняя её искусственно малым числом связей с реальностью, из-за чего вопрос поиска сходства связей станет нерешаемым для большинства детей со средней скоростью перестройки связей с мозгу. Перестань всё мерить по себе! Невозможно всех детей обеспечить мозгом олимпиадника межнаровца и учителями равными Амонашвили. Но их нужно максимально научить оперировать простыми понятиями для получения сложных выводов. А это бессмысленно делать в оторванной от имеющейся у них в мозгу картине мира. Это лишает их мотивации, это не даёт стимула мозгу физиологически правильно работать, это не даёт НИЧЕГО кроме ложно ощущения чего-то нового. Намного хуже, когда в старших классах забивают на верификацию знаний предыдущих лет на основе новых знаний. Вот это точно необходимо делать для создания цельной картины мира. Иначе механика сама по себе, а курс дифференциального и интегрального исчисления сам по себе.
А это никак не связано с повышенным количеством ненормальных среди лиц определённых родов занятий?Думаю, что связано
 Это - плата человечества за мозг, за его возможности. Биологически трудно держать мозг на грани, поэтому явно будут флуктуации и в ту, и в другую сторону. Многие здесь, на форуме, не совсем адекватно, на мой взгляд, воспринимают способности как минимум половины человечества. IQ=100 лично я воспринимаю как тормознутость небольшую. Но 100 ведь отнормировано как среднее. Т.е. практически половина населения имеет IQ МЕНЬШЕ 100! И я (имея 6-летний опыт преподавания в обычной средней школе) глубоко сомневаюсь, что подход Шурика правильнее того, что сейчас реализован в математике 7-8 классов.
Это - плата человечества за мозг, за его возможности. Биологически трудно держать мозг на грани, поэтому явно будут флуктуации и в ту, и в другую сторону. Многие здесь, на форуме, не совсем адекватно, на мой взгляд, воспринимают способности как минимум половины человечества. IQ=100 лично я воспринимаю как тормознутость небольшую. Но 100 ведь отнормировано как среднее. Т.е. практически половина населения имеет IQ МЕНЬШЕ 100! И я (имея 6-летний опыт преподавания в обычной средней школе) глубоко сомневаюсь, что подход Шурика правильнее того, что сейчас реализован в математике 7-8 классов.В квантовой механике я также не вижу геометрическую интерпретацию, от которой был бы отказ. Более того, я сдавал спецкурс "геометрические методы квантовой механики".Об изображениях в квантовой механике на школьном уровне есть очень хороший ролик
В математике вообще чем больше способов взглянуть на вещь — тем лучше.

тред только сейчас прочитал и то самый конец по-диагонали
а я согласен с Шуриком в смысле, что для продвинутого юзера Эйлер рулит.Тем более комплексные числа - великий упроститель, а сам Эйлер он типа производящей функции в рядах - весь ряд в одном мешке по-образному выражению не помню кого.
Вот у меня в мозгу немеряное количество связей и сетей и всё что тут писали, я знаю и много чего ещё
Но Эйлер проще
Я даже своим продвинутым школьникам Эйлера даю иногда. Но в школе через Эйлера не введешь конечно - все в воздухе повиснет.
В школе Эйлера на самом деле дают фактически - это триг.окружность = комплексные числа по модулю 1, которые как известно из вуза предствимы в виде z = r exp(i\phi) при r=1
Вот чо тут к Шурику приставали с sin суммы
[math]$ \cos (a+b) + i \sin (a+b) = e^{i(a+b)} = e^{ia} e^{ib} = ( \cos a + i \sin a) (\cos b + i \sin b) = (\cos a \cos b - \sin a \sin b ) + i (\cos a \sin b + \sin a \cos b)$[\math]
вот и скажите мне, что проще [math]$e^{i(a+b)} = e^{ia} e^{ib}$[\math] + формула Эйлера и [math]$i^2=-1$[\math]
или
[math]$ \cos (a+b) = \cos a \cos b - \sin a \sin b$[\math] и [math]$\sin (a+b) = \cos a \sin b + \sin a \cos b$[\math]
вы скажете последнее, ну просто вы их помните, а если нет? Что у моих студентов довольно часто, а Эйлера, что при перемножении экспонент показатели складываются и что мнимая единица в квадрате это минус 1 они знают? И вот понадобилось мне это им срочно напомнить на занятии и чо? Мне это им это рассказать как в школе нарисовав триг окружность, два угла a и b один за другим и вперёд проектируем сначала на повернутую систему координат, а потом на исходные оси и воспользовавшись проекция суммы векторов равна сумме проекций? Так это я им правила перемножения комплексных чисел геометрически напоминаю. Это же не школа, когда это первый раз выводится, тут времени нет на занятии сопли жевать, а если не напомнить самым ничего не помнящим со школы, то у них и весь новый материал повиснет в воздухе.
а уж с двойным углом всё ещё проще
[math]$e^{i2a} = (e^{ia})^2 = ( \cos a + i \sin a)^2 = \cos^2 a +2i \cos a \sin a - \sin^2 a$[\math]
[math]$ \cos 2a = \cos^2 a - \sin^2 a$[\math]
[math]$ \sin 2a = 2 \cos a \sin a$[\math]
Ну для вас это изврат, потому что как говорится "он знал, он знал!" (с)
А для моих студентов, у которых со школьной тригонометрией проблемы всё офигенно просто - вся тригонометрия в одном флаконе
И это глубокая идея у Шурика кстати. Ведь это подход Декарта если чо, метод координат, когда геометрию свели к алгебре. Давайте линейную алгебру из высшей школы выкинем для чистоты.
Я не утверждаю вслед за Шуриком, что для школьников надо вводить всё именно так, а не как исторически сложилось. Хотя прикольный был бы эксперимент построить школьную математику с нуля шиворот-навыворот и сравнить результаты.
Но между тем геометрия Евклида если аккуратно строить 25 аксиом если не ошибаюсь в школьном учебнике вскользь упоминалось (и они там не упоминались в одном месте все явно - спроси школьника - только пятый постулат наверно вспомнит по номеру. потому что через точку не лежащую на прямой единственная прямая, параллельная данной - это всё-таки на слуху, типа 2 тыс лет пытались доказать а с векторов геометрию строить - 8 аксиом ЕМНИП.
И вектора вводят в школе и на том же ЕГЭ в части стереометрии вектора здорово упрощают школьникам жизнь.
без векторного произведения правда (хотя стоило бы. а то физика вся через жопу со всеми этими правилами буравчика и левой-правой руки и прочим исторически возникшим выяснением направлений векторов силы Лоренца какой-нибудь например)
Кстати в высшей школе стоило бы кватернионы рассказать, это ведь фактически скалярное и векторное произведение в одном флаконе, типа (2+i+3j+ki-j+4k) - знай перемножай, i^2=j^2=k^2=-1, только множители нельзя местами переставлять, т.к.
ij=k, jk=i, ki=j, но
ji=-k, kj=-i, ik=-j
векторное произведение ить.
PS вот ядро Дирихле - например \sum cos kx по n от 0 до n и то же для \sum sin kx, чтобы свернуть ряд ещё надо догадаться домножить на sin x/2 и формулы преобразования произведения триг функций в суммы помнить, и у студентов с этим верёвки обычно
А \sum_0^n exp(ikx) просто сумма геометрической прогрессии и дело в шляпе сразу и для синусов и для косинусов, нужна только Эйлера и сумма прогрессии, если у студентов и с суммой прогрессии проблемы - просто домножая на 1-e^{-ix} всё посокращается, если расписать
PPS Даже ряд Фурье в комплексной форме гораздо проще триг.формы хоть они эквивалентны, например при вычислении коэффициентов ряда Фурье \int от экспоненты легче чем от произведения синусов-косинусов, тем более \exp(inx)*\exp(imx) = \exp(i(n+m)x) периодическая и интеграл не 0 будет только при n+m=0 как интеграл от константы. Конечно я даже не парю студентов при вычислении \int cos^2 x dx по периоду даже переходом к двойному углу (некоторые не помнят из школы) - просто cos^2x + sin^2 x = 1 а график sin^2 из cos^2 получен сдвигом и интеграл будет половина от интеграла от константы по периоду, но комплексная форма проще
а я согласен с Шуриком в смысле, что для продвинутого юзера Эйлер рулит.Тем более комплексные числа - великий упроститель, а сам Эйлер он типа производящей функции в рядах - весь ряд в одном мешке по-образному выражению не помню кого.
Вот у меня в мозгу немеряное количество связей и сетей и всё что тут писали, я знаю и много чего ещё
Но Эйлер проще
Я даже своим продвинутым школьникам Эйлера даю иногда. Но в школе через Эйлера не введешь конечно - все в воздухе повиснет.
В школе Эйлера на самом деле дают фактически - это триг.окружность = комплексные числа по модулю 1, которые как известно из вуза предствимы в виде z = r exp(i\phi) при r=1
Вот чо тут к Шурику приставали с sin суммы
[math]$ \cos (a+b) + i \sin (a+b) = e^{i(a+b)} = e^{ia} e^{ib} = ( \cos a + i \sin a) (\cos b + i \sin b) = (\cos a \cos b - \sin a \sin b ) + i (\cos a \sin b + \sin a \cos b)$[\math]
вот и скажите мне, что проще [math]$e^{i(a+b)} = e^{ia} e^{ib}$[\math] + формула Эйлера и [math]$i^2=-1$[\math]
или
[math]$ \cos (a+b) = \cos a \cos b - \sin a \sin b$[\math] и [math]$\sin (a+b) = \cos a \sin b + \sin a \cos b$[\math]
вы скажете последнее, ну просто вы их помните, а если нет? Что у моих студентов довольно часто, а Эйлера, что при перемножении экспонент показатели складываются и что мнимая единица в квадрате это минус 1 они знают? И вот понадобилось мне это им срочно напомнить на занятии и чо? Мне это им это рассказать как в школе нарисовав триг окружность, два угла a и b один за другим и вперёд проектируем сначала на повернутую систему координат, а потом на исходные оси и воспользовавшись проекция суммы векторов равна сумме проекций? Так это я им правила перемножения комплексных чисел геометрически напоминаю. Это же не школа, когда это первый раз выводится, тут времени нет на занятии сопли жевать, а если не напомнить самым ничего не помнящим со школы, то у них и весь новый материал повиснет в воздухе.
а уж с двойным углом всё ещё проще
[math]$e^{i2a} = (e^{ia})^2 = ( \cos a + i \sin a)^2 = \cos^2 a +2i \cos a \sin a - \sin^2 a$[\math]
[math]$ \cos 2a = \cos^2 a - \sin^2 a$[\math]
[math]$ \sin 2a = 2 \cos a \sin a$[\math]
Ну для вас это изврат, потому что как говорится "он знал, он знал!" (с)
А для моих студентов, у которых со школьной тригонометрией проблемы всё офигенно просто - вся тригонометрия в одном флаконе
И это глубокая идея у Шурика кстати. Ведь это подход Декарта если чо, метод координат, когда геометрию свели к алгебре. Давайте линейную алгебру из высшей школы выкинем для чистоты.
Я не утверждаю вслед за Шуриком, что для школьников надо вводить всё именно так, а не как исторически сложилось. Хотя прикольный был бы эксперимент построить школьную математику с нуля шиворот-навыворот и сравнить результаты.
Но между тем геометрия Евклида если аккуратно строить 25 аксиом если не ошибаюсь в школьном учебнике вскользь упоминалось (и они там не упоминались в одном месте все явно - спроси школьника - только пятый постулат наверно вспомнит по номеру. потому что через точку не лежащую на прямой единственная прямая, параллельная данной - это всё-таки на слуху, типа 2 тыс лет пытались доказать а с векторов геометрию строить - 8 аксиом ЕМНИП.
И вектора вводят в школе и на том же ЕГЭ в части стереометрии вектора здорово упрощают школьникам жизнь.
без векторного произведения правда (хотя стоило бы. а то физика вся через жопу со всеми этими правилами буравчика и левой-правой руки и прочим исторически возникшим выяснением направлений векторов силы Лоренца какой-нибудь например)
Кстати в высшей школе стоило бы кватернионы рассказать, это ведь фактически скалярное и векторное произведение в одном флаконе, типа (2+i+3j+ki-j+4k) - знай перемножай, i^2=j^2=k^2=-1, только множители нельзя местами переставлять, т.к.
ij=k, jk=i, ki=j, но
ji=-k, kj=-i, ik=-j
векторное произведение ить.
PS вот ядро Дирихле - например \sum cos kx по n от 0 до n и то же для \sum sin kx, чтобы свернуть ряд ещё надо догадаться домножить на sin x/2 и формулы преобразования произведения триг функций в суммы помнить, и у студентов с этим верёвки обычно
А \sum_0^n exp(ikx) просто сумма геометрической прогрессии и дело в шляпе сразу и для синусов и для косинусов, нужна только Эйлера и сумма прогрессии, если у студентов и с суммой прогрессии проблемы - просто домножая на 1-e^{-ix} всё посокращается, если расписать
PPS Даже ряд Фурье в комплексной форме гораздо проще триг.формы хоть они эквивалентны, например при вычислении коэффициентов ряда Фурье \int от экспоненты легче чем от произведения синусов-косинусов, тем более \exp(inx)*\exp(imx) = \exp(i(n+m)x) периодическая и интеграл не 0 будет только при n+m=0 как интеграл от константы. Конечно я даже не парю студентов при вычислении \int cos^2 x dx по периоду даже переходом к двойному углу (некоторые не помнят из школы) - просто cos^2x + sin^2 x = 1 а график sin^2 из cos^2 получен сдвигом и интеграл будет половина от интеграла от константы по периоду, но комплексная форма проще
sin(x)/cos(x)=tg(x)
а как через формулу Эйлера?
а как через формулу Эйлера?
хренасе буря в стакане...
ты видимо не прочитал первое сообщение. Никто не спорит, что комплексные числа збс, лол. Кто с этим спорил, покажи?
Читай первое сообщение: "школьников все еще мучают тригономентрическими формулами?" Человек отрицает опыт решения тригонометрических задач. Ты вот сам пишешь, что напоминаешь студентам формулу синус суммы. Зачем? Шурик вообще пишет, что она не нужна, что все через эйлера.
Вот у тебя единая картина в этом вопросе, это сразу видно, это правильно и это так и должно быть, к этому стоит стремиться. А шурик предлагает однобокую: выкинуть тригонометрию, оставить эйлера.
Ну и это если не пытаться спорить, что студентам, которые не помнят основы тригонометрии вводят "deus ex machina" в виде экспоненты. Тоже опасно звучит. Но я не преподаватель, у меня опыта нет, не знаю, что потом с такими происходит. Может в универе и нормально все.
Читай первое сообщение: "школьников все еще мучают тригономентрическими формулами?" Человек отрицает опыт решения тригонометрических задач. Ты вот сам пишешь, что напоминаешь студентам формулу синус суммы. Зачем? Шурик вообще пишет, что она не нужна, что все через эйлера.
Вот у тебя единая картина в этом вопросе, это сразу видно, это правильно и это так и должно быть, к этому стоит стремиться. А шурик предлагает однобокую: выкинуть тригонометрию, оставить эйлера.
Ну и это если не пытаться спорить, что студентам, которые не помнят основы тригонометрии вводят "deus ex machina" в виде экспоненты. Тоже опасно звучит. Но я не преподаватель, у меня опыта нет, не знаю, что потом с такими происходит. Может в универе и нормально все.
вы скажете последнее, ну просто вы их помните, а если нет? Что у моих студентов довольно часто, а Эйлера, что при перемножении экспонент показатели складываются и что мнимая единица в квадрате это минус 1 они знают? И вот понадобилось мне это им срочно напомнить на занятии и чо? Мне это им это рассказать как в школе нарисовав триг окружность, два угла a и b один за другим и вперёд проектируем сначала на повернутую систему координат, а потом на исходные оси и воспользовавшись проекция суммы векторов равна сумме проекций? Так это я им правила перемножения комплексных чисел геометрически напоминаю. Это же не школа, когда это первый раз выводится, тут времени нет на занятии сопли жевать, а если не напомнить самым ничего не помнящим со школы, то у них и весь новый материал повиснет в воздухе.Я был бы просто счастлив, если бы при прохождении комплексных чисел такое в некоторый момент проложили бы. Т.е. четко и ясно указали эту связь геометрически и алгебраически. Хотя я знал все эти формулы. В универе о таком обычно мечтать не приходится, излагают последовательность, на глубокое понимание всем срать, приходится самому догонять.
Тут какая-то подмена понятий.
Есть две разных задачи
1) Позабыв всю тригонометрию, быстро быть способным вывести основные формулы.
2) Уметь решать задачи с помощью тригонометрии.
Первая задача, пожалуй, удобнее с помощью формулы Эйлера.
Для второй задачи формула Эйлера совершенно бесполезна. По сути задача 2 в том, чтобы в оперативной памяти хранился примерный вид всех основных формул. Тогда, увидя уравнение
4 x^3- 3x = 2x\sqrt{1-x^2}, человек воскликнет - ой, а по-моему слева стоит минус синус тройного арксинуса x, а справа синус двойного арксинуса x, составит уравнение на арксинусы и получит ответ.
В школе, афаик, скорее ко второму готовят, чем к первому. В таком случае все равно тебе придется держать в уме примерный вид всех основных формул.
Так или иначе, чтобы полноценно работать с тригонометрией все основные формулы придется иметь перед глазами или в уме.
При этом знать формулу Эйлера и глядеть на синусы-косинусы с комплексной стороны - приятный бонус, но никак не полноценная замена классическому подходу
Предыдущие попытки закончились известным итогом: "Я не знаю, сколько будет 3*4, но наверное столько же, сколько 4*3"
Что же про то, как комплексные числа облегчают жизнь. Тут есть и обратная сторона - тут довольно много поворотов, которые для евклидового глаза не привычны. Неоднозначность корней и логарифмов, проблемы при возведении в степень, нехорошести с заменой области интегрирования при комплексной замене. Если человек шапочно знаком с комплексными числами, то при попытках вычислять те же обратные преобразования Фурье в комплексной форме он будет делать замены типа y=ix, не осознавая, что область интегрирования при этом из вещественной прямой перешла в мнимую. Я каждый год в теорвере при подсчете хар. функций наблюдаю, как люди пытаются брать комплексные интегралы как вещественные и в итоге получают всякую фигню.
Есть две разных задачи
1) Позабыв всю тригонометрию, быстро быть способным вывести основные формулы.
2) Уметь решать задачи с помощью тригонометрии.
Первая задача, пожалуй, удобнее с помощью формулы Эйлера.
Для второй задачи формула Эйлера совершенно бесполезна. По сути задача 2 в том, чтобы в оперативной памяти хранился примерный вид всех основных формул. Тогда, увидя уравнение
4 x^3- 3x = 2x\sqrt{1-x^2}, человек воскликнет - ой, а по-моему слева стоит минус синус тройного арксинуса x, а справа синус двойного арксинуса x, составит уравнение на арксинусы и получит ответ.
В школе, афаик, скорее ко второму готовят, чем к первому. В таком случае все равно тебе придется держать в уме примерный вид всех основных формул.
Так или иначе, чтобы полноценно работать с тригонометрией все основные формулы придется иметь перед глазами или в уме.
При этом знать формулу Эйлера и глядеть на синусы-косинусы с комплексной стороны - приятный бонус, но никак не полноценная замена классическому подходу
Я не утверждаю вслед за Шуриком, что для школьников надо вводить всё именно так, а не как исторически сложилось. Хотя прикольный был бы эксперимент построить школьную математику с нуля шиворот-навыворот и сравнить результаты.
Предыдущие попытки закончились известным итогом: "Я не знаю, сколько будет 3*4, но наверное столько же, сколько 4*3"

Что же про то, как комплексные числа облегчают жизнь. Тут есть и обратная сторона - тут довольно много поворотов, которые для евклидового глаза не привычны. Неоднозначность корней и логарифмов, проблемы при возведении в степень, нехорошести с заменой области интегрирования при комплексной замене. Если человек шапочно знаком с комплексными числами, то при попытках вычислять те же обратные преобразования Фурье в комплексной форме он будет делать замены типа y=ix, не осознавая, что область интегрирования при этом из вещественной прямой перешла в мнимую. Я каждый год в теорвере при подсчете хар. функций наблюдаю, как люди пытаются брать комплексные интегралы как вещественные и в итоге получают всякую фигню.
Хотя прикольный был бы эксперимент построить школьную математику с нуля шиворот-навыворот и сравнить результаты.Эксперименты на людях запрещены, к несчастью

Всегда выводил тригонометрические формулы через Эйлера/ряды Тейлора и примерный вид формул. Доказательства простейших формул для решения задач ведь не нужны. Один раз лишь заглянул в учебник, чтобы прочитать как их выводят для обычных людей.
Почему никто другой так не делал? Наверно потому, что это очень сильное отклонение от обычного курса (плюс нужно понимать формулу Эйлера, которую по-моему все-таки в школе не проходят) и нужно иметь уверенность, что так можно делать и удастся выкрутится из любой ситуации. Этот подход ставит тригонометрию с ног на голову, когда вместо строгих обоснований используются эвристические рассуждения. Фактически это поощряет подгонку решения под ответ. Не все могут освоить этот метод и при этом сохранить строгость рассуждений во всем остальном. Учителя просто не рискнут встать на эту дорогу. Тем школьникам, кому не удастся освоить логические рассуждения, которые постоянно придется делать при таком методе, достанется полное замешательство в голове.
Почему никто другой так не делал? Наверно потому, что это очень сильное отклонение от обычного курса (плюс нужно понимать формулу Эйлера, которую по-моему все-таки в школе не проходят) и нужно иметь уверенность, что так можно делать и удастся выкрутится из любой ситуации. Этот подход ставит тригонометрию с ног на голову, когда вместо строгих обоснований используются эвристические рассуждения. Фактически это поощряет подгонку решения под ответ. Не все могут освоить этот метод и при этом сохранить строгость рассуждений во всем остальном. Учителя просто не рискнут встать на эту дорогу. Тем школьникам, кому не удастся освоить логические рассуждения, которые постоянно придется делать при таком методе, достанется полное замешательство в голове.
Формулу Эйлера проще запомнить. Вы с этим спорите?
Мне было проще формулы для суммы и разности. Отец показал мне формулу эйлера и как эти формулы из неё получаются (может даже заставил самого вывести но я этим не пользовался и вспомнил снова только в универе.
В школе применять формулы для синусов и косинусов суммы, разности, двойного и половинного аргумента требовалось очень быстро, небе до формулы эйлера было. Это также полезно было для решения уравнений "методом при стального взгляда".
Ну и да, сейчас через 15 лет, я не все из них не вспоминю так быстро (хотя полминуты должно хватить на любую а когда вспомню возможно буду проверять эйлером или четностью для уверенности. А может просто в интернете посмотрю, это быстрее.

ghytr0001
Помню в школе мучали запоминанием тригонометрических формул. Косинус суммы и т.п. Зачем их запоминать, если есть формула Эйлера? Я уже далек от этого всего, но тут вдруг понадобилось упростить выражение, в котором стоит