Задача олимпиадная по математике
что значит "врезать"? вырезать?
аа, он не обязательно правильный
аа, он не обязательно правильный
эээ...могу,конечно,ошибаться, но т.к. угол в пятиугольник между соседними сторонами 72гр, а у правильного треугольника 60гр, то...где лопата или доп.условие в задаче?
Спасибо, уже исправил опечатку.
Пятиугольник естественно не обязан быть правильным, в условии ВСЕ сказано.
Пятиугольник естественно не обязан быть правильным, в условии ВСЕ сказано.
Ну тогда найдутся стороны, между которыми больше чем 72 градуса, там и режем...
Равносторонний пятиугольник — не значит правильный пятиугольник.
Думал, что в условии такие мелочи не стоит писать.
Думал, что в условии такие мелочи не стоит писать.
,конечно,ошибаться, но т.к. угол в пятиугольник между соседними сторонами 72гр, а у правильного треугольника 60гр, то...где лопата или доп.условие
имеется ввиду периметр=1? или что? если все стороны по 1 см.выше
Ну это просто идея без реализации, а не доказательство.
В твоих рассуждениях нигде не присутствует то, что это нечетно-угольник
Таким же образом можно "доказать" задачу и для равностороннего шестиугольника, а он вырождаться может. Так что надо еще доказать, что треугольник не "зарежется".
Кстати, эта задача мне и понравилась тем, что одновременно важна выпуклость и нечетность.
Задачу можно обобщить на любой равносторонний нечетно-угольник.
В твоих рассуждениях нигде не присутствует то, что это нечетно-угольник
Таким же образом можно "доказать" задачу и для равностороннего шестиугольника, а он вырождаться может. Так что надо еще доказать, что треугольник не "зарежется".
Кстати, эта задача мне и понравилась тем, что одновременно важна выпуклость и нечетность.
Задачу можно обобщить на любой равносторонний нечетно-угольник.
Каждая сторона в данном выпуклом равностороннем пятиугольнике равна 1.
Возьмем любую сторону AE 5угольника ABCDE.
Если на ней нельзя построить правильного треугольника, врезанного в ABCDE, значит, угол A < 60 (все в градусах BE < 1.
Угол BEE'<120, где E' - продолжение луча AE за точку E.
EBB'<120 (аналогично)
угол D достигает минимума при D in AE' и превышает 60, т.к. A<60, AB=DC=CD=1/2AD.
Т.е. D>60
аналогично C>60
=> на DC можно построить правильный треугольник
Если на ней нельзя построить правильного треугольника, врезанного в ABCDE, значит, угол A < 60 (все в градусах BE < 1.
Угол BEE'<120, где E' - продолжение луча AE за точку E.
EBB'<120 (аналогично)
угол D достигает минимума при D in AE' и превышает 60, т.к. A<60, AB=DC=CD=1/2AD.
Т.е. D>60
аналогично C>60
=> на DC можно построить правильный треугольник
Если на ней нельзя построить правильного треугольника, врезанного в ABCDE, значит, угол A < 60 (все в градусах BE < 1.Почему? Может три оставшихся стороны твой треугольник пересекают?

Тогда пятиугольник не будет выпуклым
попробуй своё "доказательство" для ромба  условия те же
условия те же
 условия те же
условия те же
Возьмем любую сторону AE 5угольника ABCDE.
Если на ней нельзя построить правильного треугольника, врезанного в ABCDE, значит, угол A < 60 (все в градусах BE < 1.
Не значит, а значит дальше не читаем
Вообще-то я не обязан контр-примеры на все рассуждения приводить (в любом случае, каждое "значит" надо обосновывать).
Но приведу контр-примерчик для разминки.
Берем вырожденный (или очень близкий к нему) пятиугольник, так чтобы получился с виду равнобедренный треугольник (боковые ребра длины 2, а основание 1 берем сторону пятиугольника — с боковой стороны треугольника смежную с основанием треугольника — для нее не значит
Извиняюсь за текст — на картинке проще бы было.
что мне непонятно, так это зачем постить бояны, которым уже 30 лет? 
http://kvant.mccme.ru/1974/06/resheniya_zadachnika_kvanta_ma...

http://kvant.mccme.ru/1974/06/resheniya_zadachnika_kvanta_ma...
Не те же 
У ромба есть одна неприятная особенность: вырожденный "ромб" (треугольник) со сторонами 2-1-1 уже пересечет треугольник, в то время как вырожденный "пятиугольник" 2-1-1-1 - не пересечет

У ромба есть одна неприятная особенность: вырожденный "ромб" (треугольник) со сторонами 2-1-1 уже пересечет треугольник, в то время как вырожденный "пятиугольник" 2-1-1-1 - не пересечет
короче, вот эта строчка
гон
Если на ней нельзя построить правильного треугольника, врезанного в ABCDE, значит, угол A < 60 (все в градусах BE < 1
гон
думаю, идея такая:
1) должно быть два тупых угла, прилегающих к одной стороне
2) один из этих углов меньше 120 градусов (если оба больше, то оставшиеся две стороны не сомкнутся)
3) на этой стороне строим треугольник
1) должно быть два тупых угла, прилегающих к одной стороне
2) один из этих углов меньше 120 градусов (если оба больше, то оставшиеся две стороны не сомкнутся)
3) на этой стороне строим треугольник
берем сторону пятиугольника — с боковой сторонынеправильный контпример

в твоем "контрпримере" МОЖНО построить треугольник на этой стороне. И далеко не один.
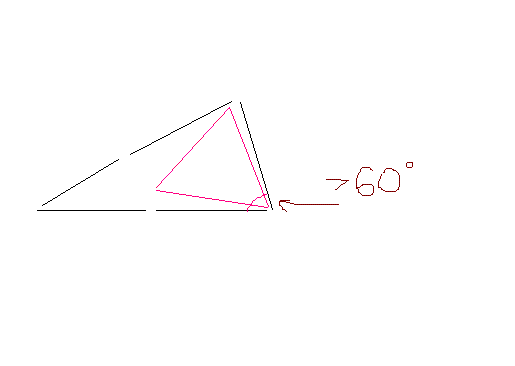
Опа, не знал 
Вообще-то мне эту задачу А.К.Ковальджи (директор лицея Вторая школа) рассказал...
Мы еще ее вместе решали...
А по какому запросу ты ее нашел в поиске — у меня не получилось
Вообще-то мне эту задачу А.К.Ковальджи (директор лицея Вторая школа) рассказал...
Мы еще ее вместе решали...
А по какому запросу ты ее нашел в поиске — у меня не получилось
тренинги по поиску у меня платные 

На стороне его построить нельзя, уголок заденет равнобедренный треугольник.
в твоем "контрпримере" МОЖНО построить треугольник на этой стороне. И далеко не один.
На стороне, если и можно построить, то только один треугольник.
да, ты прав. Если понимать "построить на стороне" так, как имел в виду я, то проблема тоже появляется.
только пункты 1) и 2) надо заменить на
1') существует сторона, к которой прилегают углы больше 60 и меньше 120 градусов
1') существует сторона, к которой прилегают углы больше 60 и меньше 120 градусов
не проходит построение.
пункты 1) и 2) надо заменить на
1') существует сторона, к которой прилегают углы больше 60 и меньше 120 градусов
контр-пример подходит
как раз все проходит
та сторона, что описывается в пункте 1') и есть основание этого вырожденного пятиугольника
как раз из-зи этого примера и надо заменить 1) и 2) на 1')
та сторона, что описывается в пункте 1') и есть основание этого вырожденного пятиугольника
как раз из-зи этого примера и надо заменить 1) и 2) на 1')
Есть три угла не меньше 60 градусов. Иначе - сумма углов < 180 * 2 + 60 * 30 = сумма углов 5иугольника.
Значит, какие-то 2 из них соседние. На стороне между ними, ясно-понятно, строится треугольник... вроде.
Значит, какие-то 2 из них соседние. На стороне между ними, ясно-понятно, строится треугольник... вроде.
ну вот и я про то же 

та сторона что описывается в моем примере, тоже подходит по описание 1').
Значит для нее твои рассуждения должны проходить тоже — но они не проходят...
Значит для нее твои рассуждения должны проходить тоже — но они не проходят...
Да опять тот же пример, та же сторона подходит под твои условия, а треугольник на этой стороне не строится...
бл$%ь, почему не проходят?
"выходит... и выходит... замечательно выходит! "
гыгы
"выходит... и выходит... замечательно выходит! "
гыгы
1) должно быть два тупых угла, прилегающих к одной стороне
2) один из этих углов меньше 120 градусов (если оба больше, то оставшиеся две стороны не сомкнутся)
3) на этой стороне строим треугольник
только пункты 1) и 2) надо заменить на
1') существует сторона, к которой прилегают углы больше 60 и меньше 120 градусов
Итого получаем:
1') существует сторона, к которой прилегают углы больше 60 и меньше 120 градусов
3) на этой стороне строим треугольник
Вот тот пример который я приводил схематично:
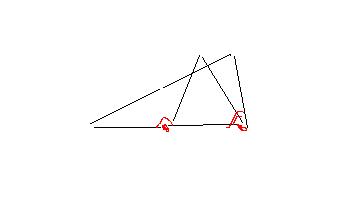
Условие 1') выполняется.
Да такая сторона существует, но так как ни чего не говорится о том случае когда таких сторон несколько, то можно выбрать любую.
Для приведенной мной стороны: с одной стороны угол в 180 градусов, а с другой тоже больше 60 градусов.
Ни чего на этой стороне не строится, а под условие она подходит. Значит этого условия не достаточно.
А то что это необходимое условие — это и так понятно, ни кто не спорит.
Не думаю, что задачка вот так просто решится, много народу пробовало найти короткое решение...
сорри, я думал, ты про основание говоришь 

Я не очень понял, с каких пор 180 < 120?
Да, это я не заметил (на вопрос то уже ответили, вот и расслабился но все равно не верю, что так просто решается.
Тогда не понятно без дополнительных рассуждений, почему условие 1') выполняется.
Тогда не понятно без дополнительных рассуждений, почему условие 1') выполняется.
условие 1' не всегда выполняется, к сожалению.
пример в студию
Нда. Действительно, всегда есть. Тогда задача решена
Нет, не решена.
Решена она будет, когда будет доказано что всегда выполняется условие 1')
Решена она будет, когда будет доказано что всегда выполняется условие 1')
Допустим не выполняется. Тогда есть 3 угла (не идущих подряд) каждый из которых либо >120 либо <60.
Пусть 5угольник ABCDE, A, B и D - соответствующие углы. A и B не могут быть одновременно >120 или <60 -
очевидно, поскольку тогда либо CE > 2 либо AE и BC пересекаются.
Пусть A < 60, B > 120. Будем увеличивать угол A, не меняя угол B. Тогда CE будет увеличиваться, значит
угол D - тоже. Будем увеличиваться, пока ситуация не нарушится (один из углов A или D не станет лежать между 60 и 120).
Поскольку оба угла увеличиваются, то есть только 2 варианта:
1. A стал равен 60. Тогда BCDE - ромб и угол CBE = углу CDE < 60. Угол ABE = 60, значит угол B (CBA) < 120. А он не менялся.
2. D стал равен 60. Тогда ABCE - ромб. Но угол AED < 180 (он не может стать больше - очевидно значит угол CBA = углу CEA < 120.
Всё плохо - противоречие.
Пусть 5угольник ABCDE, A, B и D - соответствующие углы. A и B не могут быть одновременно >120 или <60 -
очевидно, поскольку тогда либо CE > 2 либо AE и BC пересекаются.
Пусть A < 60, B > 120. Будем увеличивать угол A, не меняя угол B. Тогда CE будет увеличиваться, значит
угол D - тоже. Будем увеличиваться, пока ситуация не нарушится (один из углов A или D не станет лежать между 60 и 120).
Поскольку оба угла увеличиваются, то есть только 2 варианта:
1. A стал равен 60. Тогда BCDE - ромб и угол CBE = углу CDE < 60. Угол ABE = 60, значит угол B (CBA) < 120. А он не менялся.
2. D стал равен 60. Тогда ABCE - ромб. Но угол AED < 180 (он не может стать больше - очевидно значит угол CBA = углу CEA < 120.
Всё плохо - противоречие.
Да нет — 3 варианта!
Допустим не выполняется. Тогда есть 3 угла (не идущих подряд) каждый из которых либо >120 либо <60.
Пусть 5угольник ABCDE, A, B и D - соответствующие углы. A и B не могут быть одновременно >120 или <60 -
очевидно, поскольку тогда либо CE > 2 либо AE и BC пересекаются.
Пусть A < 60, B > 120. Будем увеличивать угол A, не меняя угол B. Тогда CE будет увеличиваться, значит угол D - тоже. Будем увеличиваться, пока ситуация не нарушится (один из углов A или D не станет лежать между 60 и 120).
Поскольку оба угла увеличиваются, то есть только 2 варианта:
...
Ты упустил случай, когда угол D > 120, но рассмотрел полностью случай когда угол D < 60.
Кроме того, в разобранных случаях угол A < 60 и угол D < 60 — но это невозможная конфигурация (не знаю как это проще доказать, быть может легче твой перебор привести, чтобы не париться при условии задачи.
Короткого доказательства в форуме пока не найдено!
А конструктивного тем более — в Кванте неконструктивно доказывается.
Последние 6 постов не читал, рассказываю то, что придумал ночью. Потом сравню с тем, что написали.
Итак. Два варианта: либо угла <60 нет, или есть.
1. Такого угла нет.
Тогда есть минимум два угла <120.
1а) они идут подряд. Два угла 60<угол<120 => на стороне между ними можно построить правильный треугольник, не пересекающийся с остальными сторонами.
1б) они чередуются. Тогда есть один угол >60, смежные углы с которым >120. В этом угле вырезаем 3угольник
2. есть угол < 60. // то есть меньше, конечно - здесь опечатка была
Тогда, как я показал выше (во втором моем посте в этом треде на противолежащей стороне можно построить треугольник.
Итак. Два варианта: либо угла <60 нет, или есть.
1. Такого угла нет.
Тогда есть минимум два угла <120.
1а) они идут подряд. Два угла 60<угол<120 => на стороне между ними можно построить правильный треугольник, не пересекающийся с остальными сторонами.
1б) они чередуются. Тогда есть один угол >60, смежные углы с которым >120. В этом угле вырезаем 3угольник
2. есть угол < 60. // то есть меньше, конечно - здесь опечатка была
Тогда, как я показал выше (во втором моем посте в этом треде на противолежащей стороне можно построить треугольник.
ну вот, застремал меня, а я был прав 

Не очень подробно написано, и возможно я упустил правильную трактовку.
Итак. Два варианта: либо угла <60 нет, или есть.
1. Такого угла нет.
Тогда есть минимум два угла <120.
1а) они идут подряд. Два угла 60<угол<120 => на стороне между ними можно построить правильный треугольник, не пересекающийся с остальными сторонами.
1б) они чередуются. Тогда есть один угол >60, смежные углы с которым >120. В этом угле вырезаем 3угольник
До пункта 1б) все правильно, вопросов нет.
В пункте 1б) можно по разному понять рассуждения:
[1]
Так как не упоминается, каким образом выбираются два угла < 120, в случае когда их больше двух, то их можно выбирать произвольно.
Если так, то берем правильный пятиугольник и любые два его не смежных угла.
Углов < 60 нет, так что мы в пункте 1.
Два угла выбрали — попали в пункт 1б но он логически не выполняется.
Может быть возможно подкорректировать формулировку пункта 1б).
[2]
Если подразумевается, что ровно два угла < 120 (все другие углы >= 120 тогда нужно рассмотреть оставшиеся случаи: 1в)...
Может я и не прав, но в любом случае, нужно пояснить что имеется ввиду.
В остальном пока разбираюсь.
Ты упустил случай, когда угол D > 120Этот случай не нужно рассматривать. Он увеличивается, но 180 равен быть не может. Значит,
он никогда не войдёт в "плохое" положение.
угла < 120`, но не смежные
Значит, если один из них A (A<120` то его соседи - В и Е - больше 120`
Тогда в A можно вырезать правильный треугольник:
построим его на стороне AB: ABK.
это можно сделать, т.к. A>60`
ABC>120` (на самом деле, достаточно, чтобы он был больше 60`)
AED>120` (достаточно условия AED > 60` + A / 2 ) => ED не пересекает AK.
AD, AC > AK, BK = CD => BK не пересекается стороной CD. Следовательно, по аксиоме кого-то на букву Ш, CD вообще не пересекает треугольник ABK. Итак, из всех сторон только AB пересекает треугольник, и она совпадает с его стороной.
Значит, если один из них A (A<120` то его соседи - В и Е - больше 120`
Тогда в A можно вырезать правильный треугольник:
построим его на стороне AB: ABK.
это можно сделать, т.к. A>60`
ABC>120` (на самом деле, достаточно, чтобы он был больше 60`)
AED>120` (достаточно условия AED > 60` + A / 2 ) => ED не пересекает AK.
AD, AC > AK, BK = CD => BK не пересекается стороной CD. Следовательно, по аксиоме кого-то на букву Ш, CD вообще не пересекает треугольник ABK. Итак, из всех сторон только AB пересекает треугольник, и она совпадает с его стороной.
Дальше, случай 2 все верно, вроде.
В ответ на:
Ты упустил случай, когда угол D > 120
Этот случай не нужно рассматривать. Он увеличивается, но 180 равен быть не может. Значит,
он никогда не войдёт в "плохое" положение.
Что значит "не нужно рассматривать" — это же доказательство, все случаи нужно рассматривать или объяснять, почему их стоит отбросить...
Объяснение тоже ни куда не годится.
Во первых, то что угол D не может достигнуть 180 можно было и доказать или хотя бы упомянуть. Но это понятно.
А во вторых, угол D не достигнет 180, но угол А достигнет 60, так что процесс остановится (да даже если бы и не остановился — с какой стати отсюда может делаться вывод о том, что можно вырезать треугольник и в этом случае ни какого противоречия не выходит.
Это все понятно.
Вопрос такой:
Случай 1б) подразумевает, что только два угла < 120, а все остальные углы >= 120?
Вопрос такой:
Случай 1б) подразумевает, что только два угла < 120, а все остальные углы >= 120?
Да. иначе бы получилась (минимум одна) пара смежных углов <120
А во вторых, угол D не достигнет 180, но угол А достигнет 60, так что процесс остановится, и в этом случае ни какого противоречия не выходитСм. пункт 1. A = 60.
не читал ваши решения, вы уже решили?
или мне свое решение запостить?
или мне свое решение запостить?
Я вроде как считаю, что решил... Но автор не согласен
Так что пость преспокойно
Так что пость преспокойно
) Пусть углов < 60 градусов ровно 2 (3 не может быть, будут соседние). Пусть A<60, C<60, тогда BE<1, BD<1, угол ABE>60, угол CBD>60 => угол EBD<60 => в треугольнике EBD сторона ED не наибольшая, но две другие стороны, как уже говорилось, меньше единицы => ED<1 - противоречие.
1) Пусть углов < 60 нет. Тогда
- либо есть >= 3 углов >120 градусов => среди них есть соседние => противоречие
- есть <= 2 углов > 120 градусов => есть >= 3 углов от 60 до 120 градусов => среди них есть соседние, на этой стороне и строим
2) Пусть теперь угол < 60 градусов есть.
а) Если углов больше 120 градусов не больше одного, то углов от 60 до 120 не меньше трех и все доказано.
б) Если углов больше 120 градусов 3 и больше, то есть соседние и противоречие
Итак, остался случай
в) Есть ровно один угол <60 и ровно два угла >120.
Пусть A>120, C>120. Если B <60, то углы E и D от 60 до 120 => сторона ED искомая.
Если же 60<B<120, то внутри угла B можно вписать треугольник. Объясню в след. посте
1) Пусть углов < 60 нет. Тогда
- либо есть >= 3 углов >120 градусов => среди них есть соседние => противоречие
- есть <= 2 углов > 120 градусов => есть >= 3 углов от 60 до 120 градусов => среди них есть соседние, на этой стороне и строим
2) Пусть теперь угол < 60 градусов есть.
а) Если углов больше 120 градусов не больше одного, то углов от 60 до 120 не меньше трех и все доказано.
б) Если углов больше 120 градусов 3 и больше, то есть соседние и противоречие
Итак, остался случай
в) Есть ровно один угол <60 и ровно два угла >120.
Пусть A>120, C>120. Если B <60, то углы E и D от 60 до 120 => сторона ED искомая.
Если же 60<B<120, то внутри угла B можно вписать треугольник. Объясню в след. посте

Интересный предельный случай:

Итак, A>120, C>120, 60<B<120.
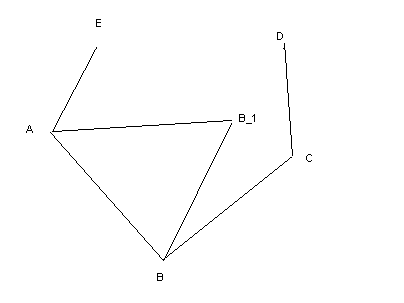
Строим правильный треугольник АВ В_1, надо доказать, что он внутрипятиугольника лежит. Ну это хз, подумать надо

Строим правильный треугольник АВ В_1, надо доказать, что он внутрипятиугольника лежит. Ну это хз, подумать надо

Я то как раз смотрел, не проходят, там такие же рассуждения, там используется то, что увеличенный угол D < 60...
См. пункт 1. A = 60.
А во вторых, угол D не достигнет 180, но угол А достигнет 60, так что процесс остановится, и в этом случае ни какого противоречия не выходит
Да, этот случай сводится к уже разобранному.
Решение принято.
Но я еще посмотрю, может пропустил чего.
Спасибо.
Решение принято.
Но я еще посмотрю, может пропустил чего.
Спасибо.
Хммм. Действительно... Тогда так. Угол D в этом случае <= 120, так как иначе угол CBE больше 120 И угол ABC > 180.
Чего быть не могло
Чего быть не могло
Ха, выкрутился
Решение принято.
Уже принято второе решение — кто нибудь может проверить их, а то я мог что то пропустить.
Сейчас третье решение почитаю.
Решение принято.
Уже принято второе решение — кто нибудь может проверить их, а то я мог что то пропустить.
Сейчас третье решение почитаю.
оно как раз и не доделано, если ты о моем 

похоже тоже решил.
Думаю, что можно доделать...
Всем спасибо.
Правда, за правильность решений не ручаюсь.
Так что, если кто найдет пробелы или ошибки в доказательствах, буду признателен.
еще осталась.
Кстати, когда учился — мы решали такие задачки на спор (символически) за шеколадку или бутылку пива (кому что больше нравится). Может возобновить традицию?
Например, я так представил евклидову плоскость в в виде дизъюнктного объединения отрезков длины 1 и 2. Правда потом кто-то сумел замостить плоскость отрезками длины 1.
Думаю, что можно доделать...
Всем спасибо.
Правда, за правильность решений не ручаюсь.
Так что, если кто найдет пробелы или ошибки в доказательствах, буду признателен.
еще осталась.
Кстати, когда учился — мы решали такие задачки на спор (символически) за шеколадку или бутылку пива (кому что больше нравится). Может возобновить традицию?
Например, я так представил евклидову плоскость в в виде дизъюнктного объединения отрезков длины 1 и 2. Правда потом кто-то сумел замостить плоскость отрезками длины 1.
чуть хитрее: отрезок - континуальное дизьюнктное обьединение канторовских множеств.

Tfrn
Дан выпуклый равносторонний, со стороной = 1, пятиугольник.Докажите, что из него можно вырезать правильный треугольник со стороной = 1.