Изобразить шестигранник, у которого 12 ребер и 8 вершин
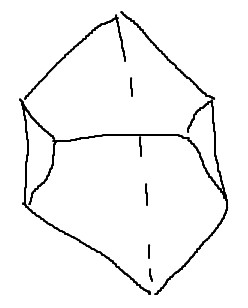- это он.все грани не четырехугольники.такого не бывает:
суммарное количество сторон рёбер останется тем же (24)
и граней столько же (6)
т.е. в среднем грань будет иметь 4 стороны
поскольку это 6-гранник, то 6-угольной грани быть не может (т.к. к ней примыкает ещё 6)
значит это 3 треугольника и 3 пятиугольника
каждый пятиугольник имеет общее ребро с каждой из остальных 5 граней
у треугольников всего 9 сторон
при этом каждый пятиугольник имеет общее ребро с каждым треугольником
т.е. все 3*3=9 сторон треугольников являются также сторонами пятиугольников
т.е. треугольники между собой не граничат
степень каждой вершины равна 3 (иначе рёбер не хватит)
значит треугольники даже не имеют общих вершин
значит вершин хотя бы 9
противоречие
от перестановки мест слагаемых сумма меняется (доказано Занусси):
"все грани не четырехугольники" non est "не все грани четырехугольники"
"все грани не четырехугольники" non est "не все грани четырехугольники"
Треугольная призма у которой вместо торцевых граней — треугольные пирамиды
Внимание, вопрос на засыпку: сколько сторон у боковых граней треугольной призмы?
Да и ребер там больше выходит
Да и ребер там больше выходит
Вместо граней пирамиды? 
да, более правильно "вместо грани — пирамида без грани"
пирамиды вытягивают носы не наружу, а внутрь.
все равно не получается 
а как от этого зависит число ребер и вершин?
ну ребро на две пирамидки можно наверно заюзать.
блин, хреново с воображенем, чую приду домой, сразу пластилин достану.
блин, хреново с воображенем, чую приду домой, сразу пластилин достану.
В + Г - Р = 2.
Это я так, на всякий случай.
Это я так, на всякий случай.
ну да 8 - 12 + Г = 2 => Г = 6.
Дальше что?
Дальше что?
Ну, вообще, не требовалась гомеоморфность сфере. Просто из этой формула она да, следует. К чему это?
Вопрос в том, что под многогранником понимать. Вроде многранники с дыркой иногда относят к многогранникам, иногда нет.
Если взять тетраэдр и из него изнутри удалить еще один тетраэдр, то будет 2*4 вершин, 2*6 ребер и все грани треугольники.
Если взять тетраэдр и из него изнутри удалить еще один тетраэдр, то будет 2*4 вершин, 2*6 ребер и все грани треугольники.
Может, у многогранника внутренность должна быть связная?
односвязная?
Зачем? Пусть просто связная, чтобы дырки, не касающиеся границы, допускать.
а, ну тогда пример подходит =)
Не, у него внутренность --- четыре несвязных тетраэдра, если я правильно его понял.
внутренность --- четыре несвязных тетраэдра, если я правильно его понял.вот я тебя вообще не понял =)
У него тетраэдр большой, из него вырезается маленький, целиком и полностью лежащий внутри большого.
Ну например возьми любой тетраэдр и сделай гомотетию с коэффициентом 2. Вот то, что между ними — и есть предложенный «многогранник».
Просто из этой формула она да, следуетда ладно? я всегда думал, что импликация в другую сторону.
Ну, если так, то потребуем еще чтобы и граница была связной 
Ну, то-есть чтобы многогранник (в смысле его внутренность) не разбивал пространство на куски
Ну, то-есть чтобы многогранник (в смысле его внутренность) не разбивал пространство на куски
да ладно? я всегда думал, что импликация в другую сторону.Ты неправильно понимайт его русский языка, йа-йа, натюрлих
Ну, если так, то потребуем еще чтобы и граница была связнойэто должно быть эквивалентно односвязности.
то-есть чтобы многогранник (в смысле его внутренность) не разбивал пространство на кускивот это уже в чистом виде односвязность =)
Ну например возьми любой тетраэдр и сделай гомотетию с коэффициентом 2. Вот то, что между ними — и есть предложенный «многогранник».Я вот думал, что он взял середины граней, соединил, и выкинул получившийся тетраэдр
это должно быть эквивалентно односвязности.Как это, а баранка многогранная?
Как это, а баранка многогранная?имхо нормально, нет?
То-есть многогранник --- такая фигулина, которую вылетев из любой точки пространства можно полностью осмотреть его поверхность. Ну и грани должны быть все плоские.
имхо нормально, нет?Так там же не все кривые можно деформировать в друг друга?
Так там же не все кривые можно деформировать в друг друга?да, я вспомнил, что путал
короче, мне засело в голову (одно из) определение односвязности для плоской области (внутренность простой кривой тоже принадлежит области и я думал, что там по аналогии. Да, это все левак. Связность границы — это то, что надо
Это эквивалентные штуки.
to ABC - афаик связность границы иногда требуют, иногда нет. Главное требование - чтобы ребро двум граням принадлежало. Но тут уж автору решать, подходит ли пример. Ну и геометры может меня зачмырят
Тор, боюсь, на 8 вершинах не построишь
to ABC - афаик связность границы иногда требуют, иногда нет. Главное требование - чтобы ребро двум граням принадлежало. Но тут уж автору решать, подходит ли пример. Ну и геометры может меня зачмырят
Тор, боюсь, на 8 вершинах не построишь
короче, мне засело в голову (одно из) определение односвязности для плоской области (внутренность простой кривой тоже принадлежит области и я думал, что там по аналогииЭто двумерно-односвязные области. То-есть любые две поверхности, натянутые на один и тот контур, можно непрерывно внутри продеформировать друг в друга. То, что я сказал, это линейно-односвязные. В последних справедлива теорема о точности 1-форм (условие полного дифференциала в первых --- теорема о точности 2-форм при условии дивергенции равной нулю (то-есть что соленоидальные поля есть роторы). Так что ты тоже прав по-своему.
to ABC - афаик связность границы иногда требуют, иногда нет. Главное требование - чтобы ребро двум граням принадлежало.Но странные же области, у которых граница несвязна
Так можно до такого сыра дойти, что мама не горюй!
Это эквивалентные штуки.это как? если мы рассматриваем только сферы, то в этом классе да. любая сфера, для которой верна эта формула, будет гомомеоморфна сфере.
А есть многогранники, не гомеоморфные сфере с каким-то числом ручек?
Листов Мебиуса захотел?
так вы сначала договоритесь, что такое многогранник
ладно, я понял, что имелось в виду
В твоем примере сколько граней?
Наверное, я все-таки фигню говорю и такую штуку называть многогранником плохо
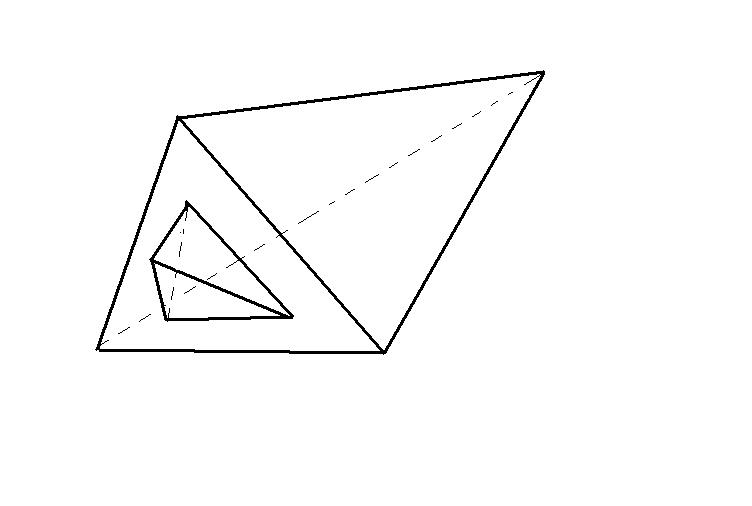
А вот такую?
заглянул в Хилтона-Уайли, пишут, что минимальное разбиение тора - 7 вершин, 21 ребро и 14 треугольников.
зы. минимальная триангуляция имелась виду.
зы. минимальная триангуляция имелась виду.
интуитивно ясно, что 8 вершин это очень много ребер
не покатит
Значение слова "Многогранник" в Большой Советской Энциклопедии:
Значение слова "Многогранник" в Большой Советской Энциклопедии:
Многогранник в трёхмерном пространстве, совокупность конечного числа плоских многоугольников, такая, что каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного называемого смежным с первым (по этой стороне); от любого из многоугольников, составляющих Многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, — к смежному с ним, и т. д. Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами Многогранника
http://bse.sci-lib.com/article077253.html ну и там дальше...в твоем рисунке нарушается "каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного)"
Приведённое определение Многогранник получает различный смысл в зависимости от того, как определить многоугольник. Если под многоугольником понимают плоские замкнутые ломаные (хотя бы и самопересекающиеся то приходят к первому определению Многогранник (вопросы, связанные с определяемыми таким образом Многогранник, будут рассмотрены в конце статьи). Основная часть статьи построена на основе второго определения Многогранник, при котором его грани являются многоугольниками, понимаемыми как части плоскости, ограниченные ломаными. С этой точки зрения Многогранник есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность некоторого геометрического тела, которое также называется Многогранник; отсюда возникает третья точка зрения на Многогранник как на геометрические тела, причём допускается также существование у этих тел «дырок», т. е. — что эти тела не односвязаны.
в твоем рисунке нарушается "каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного)"
Это где нарушается?
У меня 7 граней, 6 треугольников и один шестиугольник с дыркой. Каждая из сторон - место соприкосновения двух граней.
Когда я учился в школе, то такие шестиугольники с дыркой называли многоугольниками, ибо многоугольник - часть плоскости, ограниченная замкнутыми ломаными
Каждая из сторон - место соприкосновения двух граней.не каждая. посмотри на три ребра - место склейки маленькой пирамидки и большой
А вот такую?А тут сколько граней, каждый раз запутываюсь в подсчете
Ну да, у каждой две грани сходится. Шестиугольная и треугольная
Ну да, у каждой две грани сходится. Шестиугольная и треугольнаяНо в задаче просится шестигранник?
Я хотя бы многогранник хочу построить. 6гранников нет, уже доказали
Я хотя бы многогранник хочу построить. 6гранников нет, уже доказалиТак что, решения у исходной задачи не существует?
Странная тогда задача.
Автор треда, когда узнаешь решение, сообщи тут нам, какой ответ-то хоть!
Мне доказательство баштанова показалось убедительным, хотя я особенно над ним не думал
аа блин. точно. шестиугольная с дыркой. тогда сорри за наезд
Мне доказательство баштанова показалось убедительным, хотя я особенно над ним не думалА что, две грани могут только по двум ребрам соседничать, большим числом не могут по определению?
Я тоже не думал, надо внимательно просмотреть.
большим числом не могут по определению?Нет, могут, конечно, если многогранник невыпуклый...
Вот если так можно, то вот пример: пятиугольная пирамида, к которой на одно из ребер основания посадили еще две вершины.
Вроде 6 граней, 8 вершин, 12 ребер. Грани - 6угольник, 4 треугольника и пятиугольник
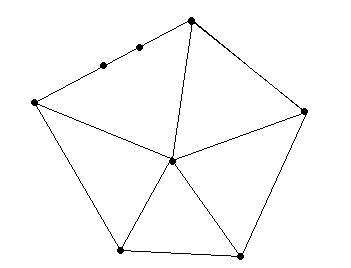
Вроде 6 граней, 8 вершин, 12 ребер. Грани - 6угольник, 4 треугольника и пятиугольник
Или нельзя брать два ребра на одной прямой?
Или нельзя брать два ребра на одной прямой?вот это точно любят запрещать.
Если взять тетраэдр и на одном ребре сделать зарубку - это как, считается?
ЗЫ. Грань есть плоская фигура, что делает устоявшееся выражение "тонкая грань" гораздо интереснее.
ЗЫ. Грань есть плоская фигура, что делает устоявшееся выражение "тонкая грань" гораздо интереснее.
Грань есть плоская фигурану, можно рассмотреть грани планарного графа на поверхности сферы.
Ой, да какая разница, третье измерение все равно не появится.
Если взять тетраэдр и на одном ребре сделать зарубку - это как, считается?имхо, не должно. Т.е. вершины не мы задаем, а они естественным образом образуются в месте пересечения ребер. А ребра — в месте пересечения граней. А если две грани лежат в одной плоскости, то не должны пересекаться. Мне кажется как-то так =) Ну можно и ребрам, лежащим на одной прямой, запретить пересекаться.
Вопрос в том, что под многогранником понимать.
есть неодносвязные шестигранники штоле?
я тормоз
кстати, а всё же сколько минимум граней (варианты: рёбер, вершин) у неодносвязного многоранника?
есть неодносвязные шестигранники штоле?а это-то тут причем? Это тут не утверждалось и не опровергалось.
кстати, а всё же сколько минимум граней (варианты: рёбер, вершин) у неодносвязного многоранника?
ээ, это минимум по всем трём параметрам?
кроме того, бывает же не тор а разность шаров например
кроме того, бывает же не тор а разность шаров например
кроме того, бывает же не тор а разность шаров напримертак вот меня выше убедили, что это какая-то другая односвязность.
ээ, это минимум по всем трём параметрам?В - Р + Г = 0
так вот меня выше убедили, что это какая-то другая односвязность.проглядел выше определения, мне они все кажутся левыми
а не левыми кажутся такие два как:
а) первая фундаментальная группа тривиальна
б) все фундаментальные группы тривиальны
нде, я знатно туплю
пожалуй, свалю из этого раздела от стыда подальше
можно и -2, тебя же не просят именно тору
т.е. у трехсвязной фигуры может меньше число вершин или ребер получиться?
Я формулу привел к тому, что на трех стульях не усидишь, т.е. все три параметра минимизировать не удастся.
Я формулу привел к тому, что на трех стульях не усидишь, т.е. все три параметра минимизировать не удастся.
насчет задачи:
задача со школьной олимпиады (московских школ) для 11 класса.
я решения не знаю.
задача со школьной олимпиады (московских школ) для 11 класса.
я решения не знаю.
задача со школьной олимпиады (московских школ) для 11 класса.Ничего себе над детишками измываются
В + Г - Р = 2 - 2g или 2 - a (вроде так, по памяти)
g - кол-во ручек, a - вол-во хуёвин (по-моему, это не точный термин) типа пришпандоренного к дырке листа мёбиуса.
Вроде бы этим исчерпываются 2-мерые односвязные многообразия, коими являются все компоненты связности
поверхности многогранника. А для многогранника (односвязного, но, возможно, с неодносвязной границей) эта величина - сумма эйлеровых характеристик для каждой компоненты связности границы.
То есть у нас, например, мог быть шар, а внутри тор или бутылка Клейна или и то и другое, либо проектвиная плоскость (a = 1 а внутри ещё одна,
но в этом случае на одну из границ всего <= 3 грани, чего явно недостаточно.
g - кол-во ручек, a - вол-во хуёвин (по-моему, это не точный термин) типа пришпандоренного к дырке листа мёбиуса.
Вроде бы этим исчерпываются 2-мерые односвязные многообразия, коими являются все компоненты связности
поверхности многогранника. А для многогранника (односвязного, но, возможно, с неодносвязной границей) эта величина - сумма эйлеровых характеристик для каждой компоненты связности границы.
То есть у нас, например, мог быть шар, а внутри тор или бутылка Клейна или и то и другое, либо проектвиная плоскость (a = 1 а внутри ещё одна,
но в этом случае на одну из границ всего <= 3 грани, чего явно недостаточно.
Взять деревянный тетраэдр и ударить несильно топором по ребру. Получится решение задачи.
Взять деревянный тетраэдр и ударить несильно топором по ребру. Получится решение задачи.А ведь действительно, подходит по всем параметрам
АФИГЕТЬ!
Так я неправильно понял сперва, подумал, что это шутка, типа расколоть надо
Респект!
Алексей всем запудрил мозги! Да! Ему тоже респект!
Так я неправильно понял сперва, подумал, что это шутка, типа расколоть надо
Респект!
Алексей всем запудрил мозги! Да! Ему тоже респект!
Кто ж знал, что грани могут соприкасаться по больше чем одному ребру!
Спасибо всем отметившимся в треде, повеселились
Спасибо всем отметившимся в треде, повеселились
Кто ж зналя знал, могли бы у меня спросить
это в какой-то конкретной школе было или во всех подряд?
Взять деревянный тетраэдр и ударить несильно топором по ребру. Получится решение задачи.нарисуйте, кому не лень, а?
Я как бы кое- что себе представил, но не могу это кое-что соотнести с
"Кто ж знал, что грани могут соприкасаться по больше чем одному ребру! "
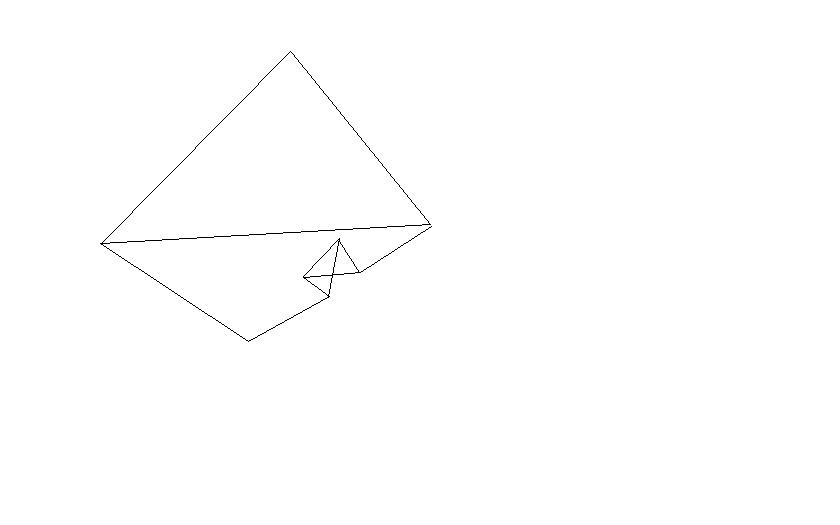
Тля... забыл одно переднее ребро дорисовать. Но, вроде понятно. Те грани исходного тетраэдра, которые были испорчены топором теперь, как видите, соприкасаются по двум ребрам.
bars70
Нужно изобразить шестигранник, у которого 12 ребер и 8 вершин(как у куба но каждая грань которого не является четырехугольником.Помогите, пожалуйста.
спасибо.