Средняя длина хорд в окружности
примерно радиус. чуть больше, конечно.
я б даже сказал пи вторых эр.
средняя арифметическая, геометрическая, еще какая?
Смело считайте и выигрывайте спор !
не-а
Вот что можно сказать:
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ ХОРДА - это частное от деления площади органов управления на их размах
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ ХОРДА - это частное от деления площади органов управления на их размах
в определении никак информация об окружности не задействована.
Мне кажется, более разумно следующее.
Начертить заранее окружность. Наловить несколько (сколько кто сможет до дед-лайна спора) представителей типа хордовых (включая людишек) , выделить хорду и поместить в окружность [если влезет целиком]. Затем в присутствии участников спора осуществить контрольные замеры, посчитать выборочное среднее и дисперсию (со Стъюдентом, естественно) и поделить вложенные в спор бабки (мне 10% за совет)
Мне кажется, более разумно следующее.
Начертить заранее окружность. Наловить несколько (сколько кто сможет до дед-лайна спора) представителей типа хордовых (включая людишек) , выделить хорду и поместить в окружность [если влезет целиком]. Затем в присутствии участников спора осуществить контрольные замеры, посчитать выборочное среднее и дисперсию (со Стъюдентом, естественно) и поделить вложенные в спор бабки (мне 10% за совет)
Когда-то в школе еще натолкнулся на эту задачу, причём читая биографию... Колчака. В своё время будущий адмирал и белый генерал тоже ее решал :-
Ответ (\frac{\pi} {2} r) уже был дан.
P.S. И если кто-то сможет посчитать эту величину в смысле отличном от среднего арифметического (среднее гармоническое и проч. то поделитесь, plz, - будет интересно посмотреть.
Ответ (\frac{\pi} {2} r) уже был дан.
P.S. И если кто-то сможет посчитать эту величину в смысле отличном от среднего арифметического (среднее гармоническое и проч. то поделитесь, plz, - будет интересно посмотреть.
[Средняя хорда * высоту (то есть диаметр)] есть площадь окружности => это площадь окружности, разделённая на диаметр, то есть (pi/2)*r, как правильно сказал Топ.
[Средняя хорда * высоту (то есть диаметр)] есть площадь окружности
1. что такое "Средняя хорда " ?
2. что такое "высота ?
3. с чего бы вдруг "[Средняя хорда * высоту (то есть диаметр)] есть площадь окружности " ?
1. что такое "Средняя хорда " ?
2. что такое "высота ?
3. с чего бы вдруг "[Средняя хорда * высоту (то есть диаметр)] есть площадь окружности " ?
хм получился ответ pi*r\4
обсчитался где-то, правильно 4r/ \pi
что значит
4r/\p?
4r/\p?
гораздо лучше (а то я уже устному счету в своем исполнении перестаю доверять)
(4*r / 3,141...) от твоего ответа отличается тем, что pi и 4 поменяны местами.
т.е.
(r*pi) / 4?
(r*pi) / 4?
есть еще вариант: r в знаменателе попробовать.
здесь пишут что pi*r/2
Там решение написано?
Если да, то пость сюда
Если нет, то считай интегралы сам внимательно.
Тогда теория меры была слабо разработана, поэтому то что там написано не есть истина в последней инстанции.
Если да, то пость сюда
Если нет, то считай интегралы сам внимательно.
Тогда теория меры была слабо разработана, поэтому то что там написано не есть истина в последней инстанции.
Если нет, то считай интегралы сам внимательно.Как я понял, автор вопроса пока никак не определил искомое понятие, и, следовательно, не знает, что (какие интегралы, и интегралы ли вообще) считать
нет автора трэда посчитал и получил пи р на 2
считал используя определение площади круга
и определение среднего арифмитического взятого в пределе по бесконечности.
считал используя определение площади круга
и определение среднего арифмитического взятого в пределе по бесконечности.
определение площади круга?
определение среднего арифмитического взятого в пределе по бесконечности.
?
Помимо "Вау!", хочется спросить: "среднего арифмитического " чего ?
автору треда.
Эта задача имеет несколько решений, взависимости от выбора "равномерной" меры на пространстве хорд.
Можно получить 4*r/ pi, можно получить \pi *r/ 4, это то что мне удалось получить, причем математически строго. Наверно, есть еще возможности.
Если автор знаком с основами теории вероятностей, то он, возможно, вспомнит парадокс Бертрана. В нем предлагается определить вероятность того, что хорда больше хорды отсекающей треть окружности. Взависимости от выбора вероятностного пространства, (сиречь меры) получались разные решения. Здесь ситуация аналогичная.
Эта задача имеет несколько решений, взависимости от выбора "равномерной" меры на пространстве хорд.
Можно получить 4*r/ pi, можно получить \pi *r/ 4, это то что мне удалось получить, причем математически строго. Наверно, есть еще возможности.
Если автор знаком с основами теории вероятностей, то он, возможно, вспомнит парадокс Бертрана. В нем предлагается определить вероятность того, что хорда больше хорды отсекающей треть окружности. Взависимости от выбора вероятностного пространства, (сиречь меры) получались разные решения. Здесь ситуация аналогичная.
все хорды можно разбить на семейства параллельных
каждое семейство получается из другого путём поворота,
т.е. достаточно посчитать среднюю хорду для одного семейства
если разбить диаметр на n щтрезков и через конец каждого провести хорду перпендикулярную диаметру
и теперь умножить каждую полученную хорду на длину отрезка разбиения и просуммировать эти произведения
взять сумму по n стремящегося к бесконечномти
получим сумму бесконечного множества площадей прямоугольников , что и есть площадь круга
отсюда найдём Сумму длин всех хорд (константа * n)
и теперь, поделив Сумму длин всех хорд на n, сократим n и получим pi*r/2
каждое семейство получается из другого путём поворота,
т.е. достаточно посчитать среднюю хорду для одного семейства
если разбить диаметр на n щтрезков и через конец каждого провести хорду перпендикулярную диаметру
и теперь умножить каждую полученную хорду на длину отрезка разбиения и просуммировать эти произведения
взять сумму по n стремящегося к бесконечномти
получим сумму бесконечного множества площадей прямоугольников , что и есть площадь круга
отсюда найдём Сумму длин всех хорд (константа * n)
и теперь, поделив Сумму длин всех хорд на n, сократим n и получим pi*r/2
с парадоксом Бертрана знаком, тоже думал сначала в этом направлении,но
всё таки , как верно здесь уже сказали
задача встретилась в биографии Деникина и именно его решение заинтересовало %)
так вот его ответ получен , спор решён
всё таки , как верно здесь уже сказали
задача встретилась в биографии Деникина и именно его решение заинтересовало %)
так вот его ответ получен , спор решён
Смил все правильно заметил насчет меры. В Вашем способе проведите хорды параллельно друг-другу - но не перпендикулярно диаметру - а под фиксированным углом. Получите ли Вы независимость решения от угла?
Эта задача имеет несколько решений
По определению, которое я дал выше, ср. геом. хорда фигуры - это площадь фигуры на ее размах (имеется в виду макс расстояние между двумя точками фигуры, т.е. "диаметр"). Размах окружности - диаметр без кавычек. Так что ответ топа единственный верный по определению
вистимо да на синус(косинус) угла как и на n тоже сократится
В том "определении", что дали Вы, длина хорды не может быть "средней" - это фиксированная для данной (наверное, односвязной) фигуры величина, если она существует.
По определению, которое я дал выше, ср. геом. хорда фигуры - это площадь фигуры на ее размах (имеется в виду макс расстояние между двумя точками фигуры, т.е. "диаметр"). Размах окружности - диаметр без кавычек. Так что ответ топа единственный верный по определениюЯ могу дать много разных определений. Собственно разные решения появляются из разных начальных определений. Твое лишь одно из многих.
в решении ошибка.
Вы слишком вольно играетесь с пределами. Вообще говоря, h зависит от n и делить на него нельзя.
Вы слишком вольно играетесь с пределами. Вообще говоря, h зависит от n и делить на него нельзя.
согласен так смело тут делить нельзя
мне вот интересно какими размышлениями руководствовался деникин получая ответ pi*r/2
мне вот интересно какими размышлениями руководствовался деникин получая ответ pi*r/2
Это не "мое" определение, а официальное определение из Народного Хозяйства!
Или вы хотите витать в облаках?
Или вы хотите витать в облаках?
Мы, конечно же ценим Ваше стремление прорекламировать Вашу компанию, - но вилите ли, если хорды проводить "под углом" - то не вся площадь круга охватывается, и если "высота" каждого "куска" будет изменяться как cos(x) - то охватываемая площадь как 2*pi-2*(2*x-1/2*sin(2x
или около того. Кроме того, и хорды можно проводить не на одинаковом расстоянии друг от друга - а по некоторому закону, могущему также служить плотностью распределения.
или около того. Кроме того, и хорды можно проводить не на одинаковом расстоянии друг от друга - а по некоторому закону, могущему также служить плотностью распределения.
это первый листок, который попался под руки, никакой рекламы %)
вообщем для чего брать хорды под углом? можно нашу систему координат повернуть ничего не поменяется
да и потом лезть в дебри со всякими "правильными понятиями" что такое средняя хорда и .т.д. я не буду
не эту цель перед собой ставил
ибо я думаю, что Деникину поставили 5 на арифметике в его школе за схожие рассуждения
вообщем для чего брать хорды под углом? можно нашу систему координат повернуть ничего не поменяется
да и потом лезть в дебри со всякими "правильными понятиями" что такое средняя хорда и .т.д. я не буду
не эту цель перед собой ставил
ибо я думаю, что Деникину поставили 5 на арифметике в его школе за схожие рассуждения
Бугага, только не Деникину, а Колчаку.
нименно деникину если верить инету %)
где-то выше я давал ссылку
где-то выше я давал ссылку
Да, но и внятного определения (помимо размаха крыл у Даже: сомневаюсь, что будущие белые генералы руководствовались определениями из энциклопеции Нархоза) не прозвучало. У Вас определение уже в методе решения, что не есть хорошё (посл. - с кавказским акцентом)
ну вообщем такого рода обсуждения,в нашем бескрайнем инете, есть в огромных количествах,
боюсь здесь начнётся что-то в таком роде,
поэтому думаю стоит закончить ибо вопрос исчерпан по-большому счёту.
боюсь здесь начнётся что-то в таком роде,
поэтому думаю стоит закончить ибо вопрос исчерпан по-большому счёту.
Еще можно проголосовать. Я - за ответ "Пи Р пополам".
Пи..Р - пополам.
-Так их, болезных !
имхо
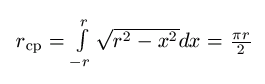
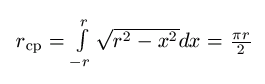
Видите ли, любезный, Ваша формула (левая часть) ничем не отличается от пол-площади и зависит от радиуса квадратично. Можно заключить, что у Вас слишком оригинальное имхо
Интеграл равен (\pi * r^2)/2. Чтобы получить среднее, нужно его пронормировать.
это и будут пол-хорды в понимании белых генералов
Эта задача имеет несколько решений, взависимости от выбора "равномерной" меры на пространстве хорд.+1.
Но с инженерной точки зрения средняя длина хорды (длина средней хорды?
) - это отношение площади фигуры к основанию (диаметру). И объясните, откуда там можно получить pi r / 4 ?P.S. Интересно-таки узнать, чьего имени всё-таки эта задача: Колчака или Деникина? Кто готов провести расследование? :-
согласен, именно пол-хорды.
ну я всего 2 минуты думал, может и не-а.
а нафига тут интегралы? ну есть ну нас бесконечное множество хорд, равно распределенных по длинне, то бишь равномерное распределение от 0 до 2*пи*р -> среднее равно (2*пи*р-0)/2= пи*р 
Это если бы окружность была бы треугольником, то они были бы равно распределены. а так хз как они распределены.
вообщем нашел в инете "Записки Боего Командира" или "Записки Белого Генерала"
не помню точно, вообщем биографию Деникина, там была задача из журнала "Математическое Общество" какого-то там года
какого-то там номера, которую Деникинскому классу предложили решить на уроке арифметики, никто кроме бравого будущего
генерала ее решить не смог, за что тот был с почестями награжден пятеркой по арифметике...
вот так
ответ Деникина: пи*эр пополам
не помню точно, вообщем биографию Деникина, там была задача из журнала "Математическое Общество" какого-то там года
какого-то там номера, которую Деникинскому классу предложили решить на уроке арифметики, никто кроме бравого будущего
генерала ее решить не смог, за что тот был с почестями награжден пятеркой по арифметике...
вот так
ответ Деникина: пи*эр пополам
а имел ли преподаватель юного Антоши, наградивший юного математика пятеркой, "свой" ответ?
об этом ни слова к сожалени.... но будем надееться что пятерку поставил не за просто так и не за командирские качества
Хм.
Я знаю три разумных способа перечислить все хорды.
1) Проводить перпедикулярно радиусу, параметр - расстояние от центра.
2) Зафиксировать один конец, параметр - угол между хордой и касательной в этой точке.
3) Зафиксировать один конец, параметр - высекаемая длина дуги.
Интересно, какая "средняя длина хорды" получится для каждого из этих способов?
Я знаю три разумных способа перечислить все хорды.
1) Проводить перпедикулярно радиусу, параметр - расстояние от центра.
2) Зафиксировать один конец, параметр - угол между хордой и касательной в этой точке.
3) Зафиксировать один конец, параметр - высекаемая длина дуги.
Интересно, какая "средняя длина хорды" получится для каждого из этих способов?
а может взять за параметр длину хорды?
тоже вариант :)
тоже вариант :)
пардон, имел ввиду
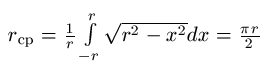
получается из
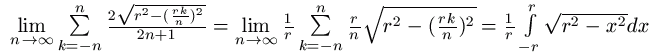
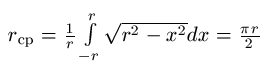
получается из
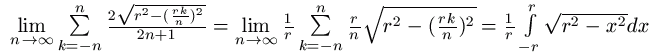
и 3 одно и то же.
я знаю еще один способ. Поместить центр окружности в начало координат. Далее рассматривать декартовы координаты центра хорды.
я знаю еще один способ. Поместить центр окружности в начало координат. Далее рассматривать декартовы координаты центра хорды.
я считал 1 способом
по второму получается 4r/pi
по второму получается 4r/pi
ботан 
(2/3) pi r
я знаю еще один способ. Поместить центр окружности в начало координат. Далее рассматривать декартовы координаты центра хорды
Тогда более сложный вопрос 
показать, в каких пределах может изменяться ответ в зависимости от выбранного метода
показать, в каких пределах может изменяться ответ в зависимости от выбранного метода(2/3) pi r
(2/3) pi r > 2r,
Ты забыл пронормировать.
у меня получилось (4/3) r
Лучше решите задачу, которую Чубариков когда-то рассказывал: Найти каблук наименьшей площади, которым можно накрыть нить длины l, бросаемую произвольным образом на плоскость
я забыл на 4 поделить
т.е. получается pi r / 6
т.е. получается pi r / 6
а что такое каблук?
Если считать "равномерной" всякую меру с массой 1, лишь бы она была инвариантной относительно группы поворотов окружности, то можно получать "средние" сколь угодно близкие к 0 и к диаметру.
Предложенные здесь методы хороши тем, что они получаются как бы "проецированием" равномерной меры на окружности, круге или диаметре.
Предложенные здесь методы хороши тем, что они получаются как бы "проецированием" равномерной меры на окружности, круге или диаметре.
Считай область, ограниченная жордановой спрямляемой кривой. Лучше, конечно, область с кусочно-гладкой границей. Можно ее двигать, чтобы накрыть нить.
Можно ее двигать, чтобы накрыть нить.Согласен, диаметр, делённый на пипополам.
Насчет естественного выбора меры. Достаточно естественно потребовать инвариантность меры относительно поворотов.
Единственная инвариантная мера на окружности -мера Лебега. Хорда задается 2-мя точками окружности, то есть точкой на торе с квадратом меры Лебега. Мне кажется, более естественную меру придумать для этой задачи нельзя.
Единственная инвариантная мера на окружности -мера Лебега. Хорда задается 2-мя точками окружности, то есть точкой на торе с квадратом меры Лебега. Мне кажется, более естественную меру придумать для этой задачи нельзя.
Если считать "равномерной" всякую меру с массой 1, лишь бы она была инвариантной относительно группы поворотов окружностиЕсли вы не знали, сообщаю - такая мера ровно одна. Так что слово " всякую" можно смело убирать
Если вы не знали, сообщаю - такая мера ровно одна.
1) Проводить перпедикулярно радиусу, параметр - расстояние от центра.
2) Зафиксировать один конец, параметр - угол между хордой и касательной в этой точке.
Или я чего-то не понимаю?
Дело вот в чем. Какие бы два параметра, однозначно определяющие хорду, вы не выбрали - через них можно найти и точки на окружности, определяющие хорду. Верно?
Далее, если в ВАШИХ параметрах определана мера, инвариантная относительно поворотов, то при переходе к точкам на окружности она обязательно перейдет в меру Лебега. Поскольку формулу замену переменной в определенном интеграле никто не отменял, то можно сразу считать параметрами точки на окружности, а мерой- меру Лебега на окружности.
Поэтому, какой бы метод подсчета среднего вы не выбрали - если он инвариантен относительно поворотов - он ОБЯЗАТЕЛьНО совпадет с ответом для меры Лебега на окружности и параметрами - пара точек на окружности. Ответ: 4 радиуса, деленные на пи.
ЛЮБОЙ другой ответ - НЕИНВАРИАНТЕН относительно поворотов, а значит неинтересен.
P.S.исправил на 4, поскольку сначала сосчитал среднюю длину ПОЛУхорды
Далее, если в ВАШИХ параметрах определана мера, инвариантная относительно поворотов, то при переходе к точкам на окружности она обязательно перейдет в меру Лебега. Поскольку формулу замену переменной в определенном интеграле никто не отменял, то можно сразу считать параметрами точки на окружности, а мерой- меру Лебега на окружности.
Поэтому, какой бы метод подсчета среднего вы не выбрали - если он инвариантен относительно поворотов - он ОБЯЗАТЕЛьНО совпадет с ответом для меры Лебега на окружности и параметрами - пара точек на окружности. Ответ: 4 радиуса, деленные на пи.
ЛЮБОЙ другой ответ - НЕИНВАРИАНТЕН относительно поворотов, а значит неинтересен.
P.S.исправил на 4, поскольку сначала сосчитал среднюю длину ПОЛУхорды
Тогда более сложный вопрос показать, в каких пределах может изменяться ответ в зависимости от выбранного методавопрос несложный: от нуля до двух радиусов. Никто не мешает брать дискретные меры.
Ну это вы зря. А если брать равномерную меру по площади в круге? Тоже что-ли получится четыре радиуса делить на пи? Тоже ж вроде случайно выбираем центр хорды!
Тоже ж вроде случайно выбираем центр хорды!На окружности такая мера ровно одна.
А я говорил про "равномерную" меру на множестве хорд. И на множестве хорд инвариантных относительно поворота мер много.
Собственно в треде было приведено 3 метода параметризации множества хорд, после чего утверждалось, что параметры распеределены равномерно и, таким образом, индуцировались разные "равномерные" меры. И все они инвариантны относительно поворотов. И все эти ответы интересны.
А я говорил про "равномерную" меру на множестве хорд. И на множестве хорд инвариантных относительно поворота мер много.
Собственно в треде было приведено 3 метода параметризации множества хорд, после чего утверждалось, что параметры распеределены равномерно и, таким образом, индуцировались разные "равномерные" меры. И все они инвариантны относительно поворотов. И все эти ответы интересны.
Нет, получится другой ответ, причем в этом треде ранее его даже написали.
Дело вот в чем. Какие бы два параметра, однозначно определяющие хорду, вы не выбрали - через них можно найти и точки на окружности, определяющие хорду. Верно?очень грубая ошибка в рассуждениях. хорде сопоставляются 2 точки на окружности, а не одна.
Далее, если в ВАШИХ параметрах определана мера, инвариантная относительно поворотов, то при переходе к точкам на окружности она обязательно перейдет в меру Лебега. Поскольку формулу замену переменной в определенном интеграле никто не отменял, то можно сразу считать параметрами точки на окружности, а мерой- меру Лебега на окружности.
s4d3v2g
вот возник спорный момент,надо посчитать среднюю длина хорд в окружности