Сложная задача по геометрии
Про случайность не понял к чему написано, почему не сказать прочто "произвольная точка на катете"?
Пусть рисонок такой:
|\
| \
|. \
|___\
. - шар.
Шар пойдёт до гипотенузы, отразится от неё вертикально вниз, отразится от катета вертикально вверх, отразится от гипотенузы и попадёт обратно в ту же точку.
Пусть рисонок такой:
|\
| \
|. \
|___\
. - шар.
Шар пойдёт до гипотенузы, отразится от неё вертикально вниз, отразится от катета вертикально вверх, отразится от гипотенузы и попадёт обратно в ту же точку.
Примечание. Единственное решение, которое я знаю, СУЩЕСТВЕННО использует случайность выбора точки.
То есть слова " точка выбрана случайно" стоят не просто так.
То есть слова " точка выбрана случайно" стоят не просто так.
Сложная но очень красивая задача по геометрии. ( $100)
Куда зайти получить $100?
Комментарий к решению. Бильярд из прямоугольного треугольнка можно заменить бильярдом из прямоугольника, составленного из двух таких прямоугольных треугольников, составленных по диагонали.
тебе бред такой не стыдно писать?
Про случайность не понял к чему написано, почему не сказать "произвольная точка на катете"?потому что я не знаю решения для произвольной точки на катете, а знаю только для случайной точки.
Шар пойдёт до гипотенузы, отразится от неё вертикально вниз, отразится от катета вертикально вверх, отразится от гипотенузы и попадёт обратно в ту же точку.это не верное рассуждение.
Куда зайти получить $100?пока никуда. написано геометрически неверное рассуждение
Комментарий к решению. Бильярд из прямоугольного треугольнка можно заменить бильярдом из прямоугольника, составленного из двух таких прямоугольных треугольников, составленных по диагонали.
Примечание. Единственное решение, которое я знаю, СУЩЕСТВЕННО использует случайность выбора точки.Тогда слова "шар обязательно вернётся в ту же точку" надо заменить на "с вероятностью 1 шар вернётся в ту же точку", то есть "мера Лебега таких точек катета, в которые шар не вернётся, равна нулю".
То есть слова " точка выбрана случайно" стоят не просто так.
Но твои слова о другом решении как-то наводит на мысль, что точки, в которые возвращение не произойдёт, всё же есть, а значит, в моём решении, похоже, кроется ошибка.
Если она есть - укажите мне на неё плиз, ибо я опять грешу тем, что читаю раздел в нетрезвом состоянии и мозг слишком уж напрягать, а тем более рисовать рисунок, выше моих сил.
это верно только для равнобедренного
тебе бред такой не стыдно писать?Неа! Вот протрезвею, тогда может и станет стыдно!
А что, правда ложанул?.. Сделаю-ка рисунок, заинтриговали блин.
А, точняк, получится не прямоугольник, а дельтоид, и лишь в случае прямоугольного треугольника этот дельтоид будет квадратом.
Признаю ошибку.
Признаю ошибку.
Задача красивая.
Но несложная
Смотри!
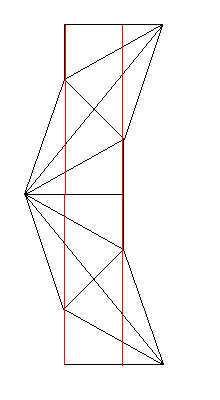
Если шар начинает свой путь между двух красных линий, то развёртка этого пути выглядит как вертикальная прямая. Которая, натурально, утыкается ровно в нужную точку.
Если же он начинает правее, то нужно нарисовать следующую картинку, в которой делается дополнительное отражение. Красивую такую, я её на бумажке нарисовал, а переносить в цифровой вид влом.
Там тоже всё совершенно очевидно.
Ну и наконец в общем случае картинка тоже рисуется, там вначале красиво так из треугольников составлена почти четверть окружности, сверху прилеплена симметричная, сверху прилеплена симметричная всей картинке. Ну, нарисуй на бумажке, мне влом опять же.
Может, я, конечно, какой крайний случай упустил. Но вроде бы всё довольно чисто. Сам себя я убедил во всяком случае.
PS: , вот именно поэтому я стараюсь не вылезать на форум в пьяном виде, чтобы с утра не стыдиться! Как бильярдный шар от стенок отражается, а?
Но несложная
Смотри!

Если шар начинает свой путь между двух красных линий, то развёртка этого пути выглядит как вертикальная прямая. Которая, натурально, утыкается ровно в нужную точку.
Если же он начинает правее, то нужно нарисовать следующую картинку, в которой делается дополнительное отражение. Красивую такую, я её на бумажке нарисовал, а переносить в цифровой вид влом.
Там тоже всё совершенно очевидно.
Ну и наконец в общем случае картинка тоже рисуется, там вначале красиво так из треугольников составлена почти четверть окружности, сверху прилеплена симметричная, сверху прилеплена симметричная всей картинке. Ну, нарисуй на бумажке, мне влом опять же.
Может, я, конечно, какой крайний случай упустил. Но вроде бы всё довольно чисто. Сам себя я убедил во всяком случае.
PS: , вот именно поэтому я стараюсь не вылезать на форум в пьяном виде, чтобы с утра не стыдиться! Как бильярдный шар от стенок отражается, а?
Если угол при катете, с которого запускается бильярдный шар, равен 30 градусам, то, замостив плоскость прямоугольными треугольниками, путем отражения треугольника относительно его катетов, мы получим замощение плоскости правильными шестиугольниками. А наша бильярдная траектория окажется лучом, параллельным стороне шестиугольника. Этот луч стартует из точки на перпендикуляре опущенном из центра шестиугольника на его сторону, параллельно этой стороне. Из геометрического рассмотрения видно, что луч пройдет через "аналогичную" точку на втором шестиугольнике от него.
Отсюда же можно получить оценку сверху на количество отражений бильярного шара от сторон треугольника, просто посчитав кол-во прямоуг. треугольников, через которые идет луч.
Отсюда же можно получить оценку сверху на количество отражений бильярного шара от сторон треугольника, просто посчитав кол-во прямоуг. треугольников, через которые идет луч.
Задача красивая.Ну да, идея-то ясна сразу: надо нарисовать развёртку. Только я её нарисовал в уме неправильно
Но несложная

До решения еще довольно далеко, но идея достроить до ромба верная. Но решение еще не близко.. сам подумай почему, если что - я попозже напишу.
Чо не близко-то?
Я ещё подумал, всё замечательно.
Ты не понял. Я не до ромба достраиваю. Вот ещё картинка, смотри!
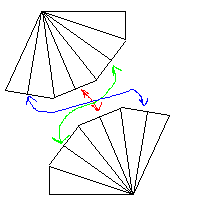
Я строю вот такую вот хрень, пока не получу более чем четверть окружности.
В зависимости от того, откуда вылетает шарик, я прилепляю симметричную хрень к нужной грани.
Потом просто и ненавязчиво отражаю всё от самой верхней стороны и получаю доказательство.
Кстати говоря, шарик везде проходит через грани правильно.
Далее, если он начинает лететь не с длинного, а с короткого катета, то тоже всё вполне очевидно. Вначале я прилепляю к треугольнику уже не четверть, а половину окружности, направленную в другую сторону. Дальше точно так же.
Я ещё подумал, всё замечательно.
Ты не понял. Я не до ромба достраиваю. Вот ещё картинка, смотри!

Я строю вот такую вот хрень, пока не получу более чем четверть окружности.
В зависимости от того, откуда вылетает шарик, я прилепляю симметричную хрень к нужной грани.
Потом просто и ненавязчиво отражаю всё от самой верхней стороны и получаю доказательство.
Кстати говоря, шарик везде проходит через грани правильно.
Далее, если он начинает лететь не с длинного, а с короткого катета, то тоже всё вполне очевидно. Вначале я прилепляю к треугольнику уже не четверть, а половину окружности, направленную в другую сторону. Дальше точно так же.
Собственно, вот для короткого катета картинка.
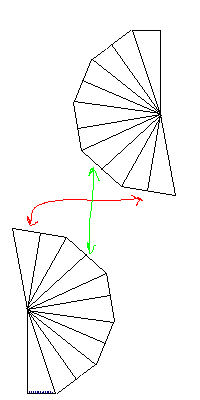
Хватит тупить, рассказывай лучше, как тебе удалось так извратиться, что стал важным вид распределения?
(EDIT: а, нет, гоню, тут ещё частный случай появляется, ща)

Хватит тупить, рассказывай лучше, как тебе удалось так извратиться, что стал важным вид распределения?
(EDIT: а, нет, гоню, тут ещё частный случай появляется, ща)
я понял, но в доказательстве есть существенный гэп, я серьезно. я могу написать где именно, но просто сам посмотри свежим взглядом.
Грубо говоря, тебе требуется равномерно ограниченное число отражений,независимо от точки. Это заведомо не так.
Грубо говоря, тебе требуется равномерно ограниченное число отражений,независимо от точки. Это заведомо не так.
Хватит тупить, рассказывай лучшеслушай, если так нервно будешь общатся, я просто буду отвечать что решение неверно, пока верное не напишешь. релакс.
Грубо говоря, тебе требуется равномерно ограниченное число отражений,независимо от точки. Это заведомо не так.Сейчас окажется, что алгебраическая природа радианной меры углов треугольника ир)рациональность, алгебраичность, скорость приближаемости рациональными) играет роль

И что мера тех углов, при которых рассуждение выше не проходит, равна нулю

И что мера тех углов, при которых рассуждение выше не проходит, равна нулюхитер сцуко) поздравляю, правда ты не до конца прав

Может быть шар, запущенный таким образом, "обстучит" все точки на катете? Если по времени его не ограничивать.
Всё, да, извини, я понял.
Да, он иногда может вылететь из построенной мной картинки. Ну, на вертикальной это особенно ясно видно, он может оказаться правее центра верхней фигни. Тогда её, верхнюю фигню, нужно ещё раз отразить, на этот раз от одной из диагоналек, а дальше я уже что-то не могу охватить внутренним взором.
Хм. С подвохом задачка!11
Да, он иногда может вылететь из построенной мной картинки. Ну, на вертикальной это особенно ясно видно, он может оказаться правее центра верхней фигни. Тогда её, верхнюю фигню, нужно ещё раз отразить, на этот раз от одной из диагоналек, а дальше я уже что-то не могу охватить внутренним взором.
Хм. С подвохом задачка!11
Может быть шар, запущенный таким образом, "обстучит" все точки на катетеЭто невозможно в принципе. Число отражений счетно.
Число отражений счетно.Зато видимо применима теорема Пуанкаре о возвращаемости, согласно которой траектория за конечное время вернётся в любую сколь угодно малую окрестность точки на трактории. Время этого возвращения будет, конечно, зависеть от размера окрестности и называется для данной окрестности временем возвращения Пуанкаре. Более того, можно построить в результате так называемое "отображение Пуанкаре", которое будет равно сдвигу вдоль траекторий на время Пуанкаре и будет отображать некую часть окрестности в себя.
тепло. не горячо, но тепло.
Сформулируй, плиз, задачу поточнее. Верно ли, что постановка задачи такова?
Определение. В прямоугольном треугольнике Т берется точка А на катете и запускается бильярдный шар из этой точки перпендикулярно катету. Говорят, что "точка А обладает свойством возвращаемости в треугольнике Т", если, испытав конечное число соударений со стенками, шар снова окажется в точке А.
Задача: доказать, что для любого прямоугольного треугольника множество точек катета, НЕ обладающих свойством возвращаемости, имеет меру Лебега, равную нулю.
Определение. В прямоугольном треугольнике Т берется точка А на катете и запускается бильярдный шар из этой точки перпендикулярно катету. Говорят, что "точка А обладает свойством возвращаемости в треугольнике Т", если, испытав конечное число соударений со стенками, шар снова окажется в точке А.
Задача: доказать, что для любого прямоугольного треугольника множество точек катета, НЕ обладающих свойством возвращаемости, имеет меру Лебега, равную нулю.
да, именно так.
Хорошо. Наконец-то появилась человеческая формулировка.
Я исправил несколько неточностей и опечаток в определении и постановке задачи. Суть не пострадала?
Я исправил несколько неточностей и опечаток в определении и постановке задачи. Суть не пострадала?
Суть не пострадала.
Ещё мыслишка пришла в голову.
Шарик летит от катета к гипотенузе и ударяется о неё. Давайте из точки соударения шарика выпустим другой шарик в сторону катета - он долетит до катета, отразится, и вернётся опять к гипотенузе, и далее полетит по пути первого катета. Получается, что траектория полёта шарика переходит в себя при сдвиге времени на константу, а именно, на время полёта шарика от катета к гипотенузе.
Шарик летит от катета к гипотенузе и ударяется о неё. Давайте из точки соударения шарика выпустим другой шарик в сторону катета - он долетит до катета, отразится, и вернётся опять к гипотенузе, и далее полетит по пути первого катета. Получается, что траектория полёта шарика переходит в себя при сдвиге времени на константу, а именно, на время полёта шарика от катета к гипотенузе.
[подсказка из зала]надо воспользоваться теоремой Пуанкаре о возвращаемости[/подсказка из зала]
Я уже упоминал об этой теореме выше в треде.
мопед не мой
Кстати, следующая задача, насколько мне известно, мировым сообществом ещё не решена:
Пусть есть треугольный биллиард. Доказать, что в нём существует по крайней мере одна периодическая траектория. То есть доказать, что найдётся хоть одна такая точка на стороне треугольника, что если из этой точки под нужным углом выпустить шар, то он после конечного числа соударений снова вернётся в эту точку и дальше полетит по пути, по которому он летел сразу после выстреливания.
Кажется, американский математик русского происхождения Анатолий Каток даже предлагает за решение сколько-то там денег, потму что ему очень интересно узнать решение, а сам он не придумал.
Пусть есть треугольный биллиард. Доказать, что в нём существует по крайней мере одна периодическая траектория. То есть доказать, что найдётся хоть одна такая точка на стороне треугольника, что если из этой точки под нужным углом выпустить шар, то он после конечного числа соударений снова вернётся в эту точку и дальше полетит по пути, по которому он летел сразу после выстреливания.
Кажется, американский математик русского происхождения Анатолий Каток даже предлагает за решение сколько-то там денег, потму что ему очень интересно узнать решение, а сам он не придумал.
применима теорема Пуанкаре о возвращаемости, согласно которой траектория за конечное время вернётся в любую сколь угодно малую окрестность точки на трактории.Причём под близким углом.
пойдет. сто баксов уже ближе.

Опять не мой мопед. Цитирую:
о теореме о возвращаемости точки фазовой траектории проходят в бесконечной близости от начальной точки. т.е бесконечно близко по координате и направлению скорости. в рациональном треугольнике возможно лишь конечное число направлений скорости. из этого следует, что в достаточно близких к начальной фазовых точках траектории направление движения будет совпадать с начальным.
теперь если запустить шарик как в условии, то он в какой-то момент будет двигаться параллельно начальному звену траектории. причем в обратном направлении. т.к. если уже сказано, что он должен двигаться в том же направлении, то ясно, что до соударения с начальным катетом но двигался в сторону этого катета. значит он после соударения начал проходить свой путь обратно и вернется в ту же точку.
что делать с нерациональными треугольниками - не ясно.
за деталями рассуждения - библиотечка квант №077.
неплохо. очень тепло.
что делать с нерациональными треугольниками - не ясно.Приблизить его рациональным.
Рациональный треугольник - это видимо такой, углы которого представляются в виде Пи умножить на рациональное число.
Приблизить его рациональным.вообще говоря жутко холодно. Если решишь, существенно это используя, дам $500. Но я бы не советовал терять время.
короче: непонятно, хз.
В посте Федечки поясняется, что траектория вернётся в малую окрестность исходной точки параллельно исходной выходящей из точки траетории. Но мне, например, не очевидно, почему она вернётся именно в саму точкук, а не просто в какую-то точку этой малой окрестности.
А ещё в гамильтоновой системе (т.е. у нас) фазовый объём сохраняется...
ладно, оставляю наедине с задачей. а то так неинтересно. буду подсказывать только если явно не в ту степь пойдешь
Кто ты, добрый филантроп и популяризатор математики на форуме МГУ?
добрый филантропты заблуждаешься. но ты пока еще этого не понял

теорема Ферма тоже просто формулируется
ты заблуждаешься. но ты пока еще этого не понялТипа твой гонорар за придуманное нами решение задачи сильно превысит и 100, и 500 баксов? Но ты же говоришь, что решение задачи тебе и так известно. Неужели ты врёшь и хочешь подзаработать на своих же мгушных товарищах?

Если честно, задор решать задачку как-то поубавился 

что-то у тебя дедукция сильно страдает, или нервы. скорее первое)
успокойся, никаких подлых мыслишек у меня нет
успокойся, никаких подлых мыслишек у меня нет

Но ты же говоришь, что решение задачи тебе и так известно. Неужели ты врёшьну если есть желание, в приват могу написать. естессно если пообещаешь никому не рассказывать. просто уже пара верных мыслей прозвучала, ну как знаешь в общем)
Просто неприятно как-то прозвучали вот эти твои слова
типа - ты дурачок и делаешь глупости, но пока ещё этого не понял, потому что дурачок
Ладно, проехали.
ты заблуждаешься. но ты пока еще этого не понял
типа - ты дурачок и делаешь глупости, но пока ещё этого не понял, потому что дурачок

Ладно, проехали.
Если правда знаешь решение, то не шли в приват - ещё немного подумаю перед сном.
Если правдатебя флокал что ли приучил к мысли что все вокруг врут?
 хотя да, немудрено
хотя да, немудреноПросто неприятно как-то прозвучали вот эти твои словакороче, правильно их нужно понимать так:
задаче непростая, но решабельная.
Человеку который ее решит мне нежалко подарить 100 баксов, потому что это явно будет не быдло.
Человеку который ее решит мне нежалко подарить 100 баксов, потому что это явно будет не быдло.Хорошо, теперь понятна мотивация твоего поста.
Давай чтоб тебе не скучно было тоже загадаю задачку. Решить обязательно школьными методами, а точнее - методами школьной геометрии. Задача довольно простая, но всё же забавная. Мне лично очень мешали её решать знания из матанализа, теории функций, топологии, и аналитической геометрии.
Определние. Окружность - все точки плоскости, удалённые от одной выбранной (центра) на расстояние R, точки, расстояние от которых до центра больше R, называются лежащими вне окружности, а меньше R - внутри окружности.
Задача. Доказать, что хорда лежит внутри окружности.
Мне известно 3 школьных решения этой задачи, одно из которых придумал я сам вчера, одно - мой товарищ-школьник, а одно сообил нам мой сокурсник, который и загадал задачу.
ну первое что в голову пришло - по теореме пифагора для точек хорды и тому факту что перпендикуляр является кратчайшим отрезком. Вроде все школьное?
Я, конечно, темный шо пипец, но, по-моему, факт, что
![[math]$|c \vec a +(1-c) \vec b|\leq r $[/math]](mathimg.php?math=%24%7Cc%20%5Cvec%20a%20%2B%281-c%29%20%5Cvec%20b%7C%5Cleq%20r%20%24) при всех неотрицательных c следует прямо из неравенства треугольника?
при всех неотрицательных c следует прямо из неравенства треугольника?
Да, теорема Пифагора используется в одном из решений.
Если хочешь, чтобы я проверил твоё решение, напиши плиз его подробно, с обозначениями и желательно рисунком. Но в общем-то задача достаточно простая, чтобы можно было проверить и самому.
Можешь поискать ещё решения Ещё есть решение, опирающееся на теорему косинусов, а я придумал решение, опирающееся на то, что в треугольнике против большей стороны лежит больший угол.
Ещё есть решение, опирающееся на теорему косинусов, а я придумал решение, опирающееся на то, что в треугольнике против большей стороны лежит больший угол.
Если хочешь, чтобы я проверил твоё решение, напиши плиз его подробно, с обозначениями и желательно рисунком. Но в общем-то задача достаточно простая, чтобы можно было проверить и самому.
Можешь поискать ещё решения
 Ещё есть решение, опирающееся на теорему косинусов, а я придумал решение, опирающееся на то, что в треугольнике против большей стороны лежит больший угол.
Ещё есть решение, опирающееся на теорему косинусов, а я придумал решение, опирающееся на то, что в треугольнике против большей стороны лежит больший угол.мне напомнило это реальный случай.
рассказываю уравнение окружности, и спрашиваю потом : "а как вы думаете, почему окружность действительно задается этим уравнением?"
Лес поднятых рук и все радостно говорят "потому что вы так сказали."
Стал обьяснять, нарисовал рисунок, теорема Пифагора итд. На первой парте сидит студентка и восхищенно покачивая головой говорит : - so smart...
рассказываю уравнение окружности, и спрашиваю потом : "а как вы думаете, почему окружность действительно задается этим уравнением?"
Лес поднятых рук и все радостно говорят "потому что вы так сказали."
Стал обьяснять, нарисовал рисунок, теорема Пифагора итд. На первой парте сидит студентка и восхищенно покачивая головой говорит : - so smart...
при всех неотрицательных cДаже если с огромно?
рассказываю уравнение окружности, и спрашиваю потом : "а как вы думаете, почему окружность действительно задается этим уравнением?"Чёрт возьми, если ты определил окружность как множество точек, координаты которых удовлетворяют какому-то там уравнению, то ребята с поднятыми руками абсолютно правы. Только вместо "вы так сказали" точнее было бы сказать "вы так определили", но в вольной речи "вы так сказали" куда уместнее.
Лес поднятых рук и все радостно говорят "потому что вы так сказали."
я ничто вообще не определял по правде говоря, потому что самый частый вопрос: "будет ли это на экзамене?". вообще по любому поводу. на экзамене только уравнение окружности было, а геометрического определения не было)
Определение. В прямоугольном треугольнике Т берется точка А на катете и запускается бильярдный шар из этой точки перпендикулярно катету. Говорят, что "точка А обладает свойством возвращаемости в треугольнике Т", если, испытав конечное число соударений со стенками, шар снова окажется в точке А.Я кажется доказал, что в любом треугольнике, а не только прямоугольном, на любой стороне множество точек, обладающих свойством возвращаемости, всюду плотно.
Задача: доказать, что для любого прямоугольного треугольника множество точек катета, НЕ обладающих свойством возвращаемости, имеет меру Лебега, равную нулю.
Но как извлечь из этого то, что нужно, пока не понимаю.
А где преподаёшь-то?
в любом треугольнике, а не только прямоугольном, на любой стороне множество точек, обладающих свойством возвращаемости, всюду плотно.Решения задачи Катка о существовании периодической траектории это, естственно, не даёт, поскольку траектория может возвращаться в точку под другим углом.
В посте Федечки поясняется, что траектория вернётся в малую окрестность исходной точки параллельно исходной выходящей из точки траетории. Но мне, например, не очевидно, почему она вернётся именно в саму точкук, а не просто в какую-то точку этой малой окрестности.Если мы вернулись перпердикулярно катету в другую точку на нём, то дальше мы проделаем тот же путь в обратном направлении и попадём в исходную точку. Так что можно следить только за направлением.
Если мы вернулись перпердикулярно катету в другую точку на нём, то дальше мы проделаем тот же путь в обратном направлении и попадём в исходную точку. Так что можно следить только за направлением.сильно, что я могу сказать.
Таким образом, для треугольников, углы которых выражаются рациональными долями Пи, задача решена.
да, совершенно верно. к сожалению это слабо помогает в общем случае. прямо скажем - никак не помогает 

Ты ничего не попутал? Рассмотри точки основания высот, запусти из одной в другую. Твой шар будет ровно по этим 3 точкам прыгать независимо от треугольника.
Пусть есть треугольный биллиард. Доказать, что в нём существует по крайней мере одна периодическая траектория. То есть доказать, что найдётся хоть одна такая точка на стороне треугольника, что если из этой точки под нужным углом выпустить шар, то он после конечного числа соударений снова вернётся в эту точку и дальше полетит по пути, по которому он летел сразу после выстреливания.
Чего?..
А случай тупоугольного треугольника?
Он и представляет основной интерес.
Я заметил, что с тупоугольным не работает. Правда после того, как спать пошел. Почему сразу в условии не написать, что это именно для тупоугольных наибольший интерес?
Почему сразу в условии не написать, что это именно для тупоугольных наибольший интерес?ну, могу так сказать( имхо) : разделение отдельно на остроугольный и тупоугольный случай в каком то смысле неестественно и сбивает с правильного пути.
Например для рациональных треугольников тоже все доказано, но думается что неправильно будет в задаче упоминать что нужно именно для иррациональных доказывать.

491593
В прямоугольном треугольнике случайно берется точка на катете ( случайно относительно меры Лебега) и запускается бильярдный шар из этой точки перпендикулярно катету. Шар обязательно вернется ровно в ту же точку.