Ответы на вопросы по дифференциальной геометрии
Какого из великих математиков следует считать родоначальником дифференциальной геометрии?
Когда этот раздел геометрии оформился в самостоятельное направление в математике?
Мне интересно
Когда этот раздел геометрии оформился в самостоятельное направление в математике?
Мне интересно

Гаусс безусловно.
В 18 веке.
Сейчас классическая дифф.геометрия плавно слилась с матанализом в новую науку - геометрический анализ, родоначальником которой стоит считать великого китайского математика Яу.
Но вообще я предолагал не исторический ликбез устроить а предметную по возможности свободного времени помощь - знаю что многим она дается с определенным трудом.
В 18 веке.
Сейчас классическая дифф.геометрия плавно слилась с матанализом в новую науку - геометрический анализ, родоначальником которой стоит считать великого китайского математика Яу.
Но вообще я предолагал не исторический ликбез устроить а предметную по возможности свободного времени помощь - знаю что многим она дается с определенным трудом.
Вот скажите, Учитель, обычно разного рода "хорошие" поточные интегралы. (например, в физике, к которой относится мой диплом о высшем образовании) ассоциируют с интегралом от какой-нибудь k-формы по соотв. поверрхности.
Например, импульс есть интеграл от тензора энергии импульса по пространственноподобной поверхности (простр. Минковского с сигнатурой +---... что обычно записывается как
P^{\mu}=\int T^{\mu \nu} dS_{\nu}
В случае, когда поверхность имеет "нормируемую" нормаль n_{\nu}, dS_{\nu} имеет смысл n_{\nu}*{площадь инфинитезимальной площадки}.
Допустим, я хочу вычислить поток от T^{\mu \nu} (симметр. тензор, гладкий всюду, где я интегрирую) по светоподобной гиперповерхности (световому конусу для определенности). Там квадрат "нормали" равен нулю.
Вопрос простой: можно ли корректно ассоциировать запись \int T^{\mu \nu} dS_{\nu} (\mu — фиксированная координата) с интегралом от формы, т.е. корректно определить эту запись?
Например, импульс есть интеграл от тензора энергии импульса по пространственноподобной поверхности (простр. Минковского с сигнатурой +---... что обычно записывается как
P^{\mu}=\int T^{\mu \nu} dS_{\nu}
В случае, когда поверхность имеет "нормируемую" нормаль n_{\nu}, dS_{\nu} имеет смысл n_{\nu}*{площадь инфинитезимальной площадки}.
Допустим, я хочу вычислить поток от T^{\mu \nu} (симметр. тензор, гладкий всюду, где я интегрирую) по светоподобной гиперповерхности (световому конусу для определенности). Там квадрат "нормали" равен нулю.
Вопрос простой: можно ли корректно ассоциировать запись \int T^{\mu \nu} dS_{\nu} (\mu — фиксированная координата) с интегралом от формы, т.е. корректно определить эту запись?
спасибо за вопрос, я его пока совершенно не понял, дайте мне время 'вьехать' , попозжа отвечу 

Вот скажите, Учитель, обычно разного рода "хорошие" поточные интегралы. (например, в физике, к которой относится мой диплом о высшем образовании) ассоциируют с интегралом от какой-нибудь k-формы по соотв. поверрхности.
Например, импульс есть интеграл от тензора энергии импульса по пространственноподобной поверхности (простр. Минковского с сигнатурой +---... что обычно записывается как
![[math]$P^{\mu}=\int T^{\mu \nu} dS_{\nu}$[/math]](mathimg.php?math=%24P%5E%7B%5Cmu%7D%3D%5Cint%20T%5E%7B%5Cmu%20%5Cnu%7D%20dS_%7B%5Cnu%7D%24)
В случае, когда поверхность имеет "нормируемую" нормаль![[math]$n_{\nu}, dS_{\nu}$[/math]](mathimg.php?math=%24n_%7B%5Cnu%7D%2C%20dS_%7B%5Cnu%7D%24) имеет смысл
имеет смысл ![[math]$n_{\nu}$[/math]](mathimg.php?math=%24n_%7B%5Cnu%7D%24) *{площадь инфинитезимальной площадки}.
*{площадь инфинитезимальной площадки}.
Допустим, я хочу вычислить поток от![[math]$T^{\mu \nu}$[/math]](mathimg.php?math=%24T%5E%7B%5Cmu%20%5Cnu%7D%24) (симметр. тензор, гладкий всюду, где я интегрирую) по светоподобной гиперповерхности (световому конусу для определенности). Там квадрат "нормали" равен нулю.
(симметр. тензор, гладкий всюду, где я интегрирую) по светоподобной гиперповерхности (световому конусу для определенности). Там квадрат "нормали" равен нулю.
Вопрос простой: можно ли корректно ассоциировать запись![[math]$\int T^{\mu \nu} dS_{\nu}$[/math]](mathimg.php?math=%24%5Cint%20T%5E%7B%5Cmu%20%5Cnu%7D%20dS_%7B%5Cnu%7D%24) (\mu — фиксированная координата) с интегралом от формы, т.е. корректно определить эту запись?[/quote]
(\mu — фиксированная координата) с интегралом от формы, т.е. корректно определить эту запись?[/quote]
Например, импульс есть интеграл от тензора энергии импульса по пространственноподобной поверхности (простр. Минковского с сигнатурой +---... что обычно записывается как
В случае, когда поверхность имеет "нормируемую" нормаль
Допустим, я хочу вычислить поток от
Вопрос простой: можно ли корректно ассоциировать запись
При первом зафиксированном индексе тензорное поле ![[math]$ T^{\mu \nu} $[/math]](mathimg.php?math=%24%20T%5E%7B%5Cmu%20%5Cnu%7D%20%24) становится векторным. Если в пространстве есть обьем ( кососимметрическая 4-форма то это векторное поле сворачивается по одному индексу с обьемом и получается 3 форма, которая и интегрируется по 3-мерной границе 4-мерного тела. Именно это и происходит при скалярном умножении вектора на нормаль.
становится векторным. Если в пространстве есть обьем ( кососимметрическая 4-форма то это векторное поле сворачивается по одному индексу с обьемом и получается 3 форма, которая и интегрируется по 3-мерной границе 4-мерного тела. Именно это и происходит при скалярном умножении вектора на нормаль.
В случае 4-мерного пространства Минковского проблема ни в том, что иногда нет нормали, а в том что нет обьема. Не с чем свертывать векторное поле. Поэтому я не вижу как придать корректный смысл последнему интегралу.
В случае 4-мерного пространства Минковского проблема ни в том, что иногда нет нормали, а в том что нет обьема. Не с чем свертывать векторное поле. Поэтому я не вижу как придать корректный смысл последнему интегралу.
можно ли причесать Ежа, о Учитель!
Не совсем тогда понятно (точнее, совсем не понятно почему в минковском нет формы объема? Как это следует из определений и чем попытка ее построения отличается от 4-евклида?
Как же тогда основное понятие в лагранжевом подходе к теории поля — действие — как интеграл от скаляра (гордо именуемого лагранжианом) по 4-объему, вообще бессмысленно ?
Вот, например, запись физиков действия действителного скалярного поля:
S=1/2*\int \partial_{\nu}\phi(x) \partial^{\nu}\phi (x) d^4 x
(инт. по всему минковскому)
Как же тогда основное понятие в лагранжевом подходе к теории поля — действие — как интеграл от скаляра (гордо именуемого лагранжианом) по 4-объему, вообще бессмысленно ?
Вот, например, запись физиков действия действителного скалярного поля:
S=1/2*\int \partial_{\nu}\phi(x) \partial^{\nu}\phi (x) d^4 x
(инт. по всему минковскому)
угу, вопрос(ы) понял, щас пока занят, чуть позже отвечу.
to Шерстяной: Ежа причесать - Нельзя! Ключевые слова - индекс векторного поля, эйлерова характеристика.
to Шерстяной: Ежа причесать - Нельзя! Ключевые слова - индекс векторного поля, эйлерова характеристика.
эйлерова характеристикаа подробнее, плиз!
что такое эйлерова хар-ка для ежа?
Не совсем тогда понятно (точнее, совсем не понятно почему в минковском нет формы объема? Как это следует из определений и чем попытка ее построения отличается от 4-евклида?Обьем в пространстве Минковского определен, но никак не связан с метрикой Минковского. Он определяется просто если отождествить пространство Минковского с 4-мерным Евклидовым, забыв про псевдометрику вообще.
Метрический обьем в евклидовом пространстве определяется так : рассмотрим базис из 4 ортонормальных векторов. Форма обьема взятая от этой четверки равна единице. То есть определение существенно использует евклидову метрику.
Однако этот евклидов обьем будет хорошо определен и на пространстве Минковского, в силу того что группа преобразований Лоренца будет его сохранять( определитель матриц Лоренца по модуля равен единице).
Просто мне внутренне не нравится, что в определении не используется псевдометрика.
Далее, возвращаясь к первому вопросу про тензор энергии- импульса, 'нормаль' определена будет не всегда, но подынтегральное выражение можно понимать как свертку векторного поля с 4-обьемом, что даст 3-форму, которую можно интегрировать по 3-мерной границе, как уже было сказано. Но, повторюсь, метрики Минковского здесь нет.
Вот, например, запись физиков действия действителного скалярного поля:Здесь, в отличие от первого случая, все хорошо. Метрика Минковского скрыта в подынтегральном выражении. В нем идет свертка по верхним и нижним индексам, но в членах с верхними индексами оные были предварительно подняты из нижних путем свертки с метрическим тензором Минковского.
(инт. по всему минковскому)
Попытался написать подробно как мог, уточню что-либо по написанному если возникнут вопросы.
что такое эйлерова хар-ка для ежасчитаем лысого ежа сферой.

в определении не используется псевдометрикаПочему же, используется:
где
Просто в случае метрики Минковского, как и в случае евклидовой,
в отличие от ОТО, например.
Хм, спасибо за уточнение, не знал. Да, это по сути означает что вместо четверки ортонормальных векторов берем четверку псевдоортонормальных как элемент единичного обьема.
пока новых вопросов нет, запощу немного развлекательного ликбеза.. Ведущий современный специалист по дифференциальной геометрии, единственный китайский филдсовский лауреат Шин-Тун Яу


что ты этим хотел сказать?
Топик подразумевает присутствие людей, у которых есть вопросы по диффгему по учебе или из личного интереса к науке. Знаменитые геометры прошлого Гаусс, Риман, Пуанкаре и так многим известны. Но нужно знать и героев нашего времени.
(1) Дайте, пожалуйста, простое, наглядное и инвариантное определение (G,X)-согласованности связности на (G,X)-расслоении p:E->B, где G, X, E, B - соответственно группа рассоения, слой, пространство рассл-я и база рассл-я.
(2) Прозрачное и инвариантное определение кривизны связности локально тривиального расслоения.
(2) Прозрачное и инвариантное определение кривизны связности локально тривиального расслоения.
спасибо за вопрос, сейчас занят, развернуто отвечу попозже.
вкратце:
1) Связность - это способ 'связать' (соединить) друг с другом различные слои расслоения. Отсюда и слово.
2) Кривизна связности - это тензор, который показывает, насколько локальный параллельный перенос в слоях зависит от выбранного пути.
Оба вопроса позволяют дать очень наглядный, геометрически ясный ответ, который напишу попозже.
вкратце:
1) Связность - это способ 'связать' (соединить) друг с другом различные слои расслоения. Отсюда и слово.
2) Кривизна связности - это тензор, который показывает, насколько локальный параллельный перенос в слоях зависит от выбранного пути.
Оба вопроса позволяют дать очень наглядный, геометрически ясный ответ, который напишу попозже.
Связность - это способ 'связать' (соединить) друг с другом различные слои расслоения.интересная этимология

Жду Вашего ответа.
расскажи основную идею суперструн.
расскажи основную идею суперструн.вообще это скорее к rogdin-у ( касательно физического смысла ). Дифференциально-геометрический set up чуть позже напишу.
Как наглядно представить себе пространство Минковского (например, R_{1,1} особенно искривлённое? Аналогии интервала с евклидовым расстоянием не хватает: объекты, отличающиеся на поворот в евклидовом пространстве, естественно воспринимаются как равные, а для пространства Минковского - хрен.
Может есть какие-то ещё "картинки"?
(всё главным образом в контексте СТО и ОТО)
Может есть какие-то ещё "картинки"?
(всё главным образом в контексте СТО и ОТО)
постараюсь ответить попозже. рад такому кол-ву вопросов.
Поскольку несколько вопросов уже прозвучало, связанных с псевдоевклидовым пространством, то нужно запостить для общей эрудиции. Немецкий математик русского происхождения Герман Минковский.


А ведь раньше аспиранты устраивали консультации в читалке 6-ого корпуса ФДС  Сейчас опустились до форума
Сейчас опустились до форума 

 Сейчас опустились до форума
Сейчас опустились до форума 

А ведь раньше аспиранты устраивали консультации в читалке 6-ого корпуса ФДСя физически не могу там быть

Если ты серьезно хочешь сделать тред, в котором можно будет обсуждать диф. геом., то это круто. Предлагаю тогда снести имеющийся и сделать новый, удобный и обсуждаемый. Соответственно поднятые темы сделать там в качестве нескольких вопросов. Прикреплять его не стоит, но я его по-крайней мере кипну и мб, если появятся желающие сделать аналогичное по другим дисциплинам - закину ссылки в ФАК
ПС Отключать ПМки от модераторов - не очень разумно, тем паче, что я тебе в ПМ не флудил вроде никогда...
ПС Отключать ПМки от модераторов - не очень разумно, тем паче, что я тебе в ПМ не флудил вроде никогда...
Я понял, я предлагаю сначала оставить все как есть на некоторое время, а потом, если появятся более-менее регулярные посетители, устроить голосовалку как удобнее - обсуждаемый тред или нет.
Обсуждаемый тред удобен когда есть четко разделяемые по смыслу посты ( напр. фотографии или анекдоты а в дифф. геометрии многие вопросы сильно пересекаются.
Обсуждаемый тред удобен когда есть четко разделяемые по смыслу посты ( напр. фотографии или анекдоты а в дифф. геометрии многие вопросы сильно пересекаются.
Дайте, пожалуйста, простое, наглядное и инвариантное определение (G,X)-согласованности связности на (G,X)-расслоении p:E->B, где G, X, E, B - соответственно группа рассоения, слой, пространство рассл-я и база рассл-я.Предположим, что есть расслоение p:E-->B и Г - некое сечение этого расслоения, то есть неформально говоря гладкая функция, заданная на базе расслоения, со значениями в слоях.
Также предположем, что у нас есть некий вектор V в касательном пространстве к точке 'x' в базе расслоения и мы хотим продифференцировать Г вдоль вектора V.
Но что значит продифференцировать - это в частности означает вычислить изменение значений Г при малом смещении вдоль V. Но ведь значения Г лежат в разных слоях, как их сравнить? Значит нужно уметь отождествлять (связывать) слои вдоль вектора V. Причем отождествление разумно сделать линейным ( по слою расслоения и по вектору ) и удовлетворяющим формуле Лейбница. Способ отождествления ( он неединственен) и называется связностью.
Предположем теперь, что на слоях (Х) расслоения задана некая дополнительная структура ( евклидова, псевдоевклидова, симплектическая итд..) которая сохраняется при действии группы G. Связность вполне разумно назвать (G,Х) - согласованной, если то самое отождествление слоев, описанное выше, тоже сохраняет эту дополнительную структуру.
Пример. На Римановом многообразии так называемая связность Леви-Чивита на касательном расслоении сохраняет дополнительную структуру - а именно риманову метрику, то есть является ( (О(n R^n)-согласованной.
(2) Прозрачное и инвариантное определение кривизны связности локально тривиального расслоения.Пусть
Так же рассмотрим следующий линейный оператор на слоях в этой окрестности, в каждой точке билинейно зависящий от векторов X и Y:
Если бы наше расслоение и связность было тривиальными, то оператор
Однако расслоение и связность нетривиальны, или, иными словами искривлены, а значит оператор
Аналогии интервала с евклидовым расстоянием не хватает: объекты, отличающиеся на поворот в евклидовом пространстве, естественно воспринимаются как равные, а для пространства Минковского - хрен.Предположим мы находимся на евклидовой плоскости или в трехмерном евклидовом пространстве. Возмите любой вектор и рассмотрите его орбиту под действием группы изометрий пространства, то есть все вектора такой же длины ( если группа на них действует транзитивно). На плоскости вы получите окружность, в пространстве сферу.
Проделайте такую же операцию на псевдоевклидовой плоскости - вы получите расслоение плоскости на гиперболы - псевдосферы. Поупражняйтесь с ними мысленно - как бы ' погуляйте' по ним. Посмотрите например что будет происходить с какой нибудь точкой пространства под действием степеней какого нибудь одного отображения из группы Лоренца ( это соответствует прыжкам по окружности на один и тот же угол в евклидовой плоскости). Hope this helps.
расскажи основную идею суперструн.про физический смысл лучше безусловно спросить у rogdin-а. Математически - вместо точки элемантарным обьектом считаем окружность или отрезок. Значит вместо одномерной траектории точки мы получим двумерную поверхность в качестве аналога мировой линии частицы.
Чтобы этот обьект изучать нужно задать действие, а потом его минимизировать. Такое действие задается двуя эквивалентными способами - действие Намбу-Гато и действие Полякова. Если интересно более подробно, то можешь посмотреть действие Намбу-Гато или Полякова в гугле и если что-нибудь будет непонятно, я попробую помочь.
Небольшой развлекательный ликбез в связи с вопросом про связности. Математик, внесший существенный вклад в концепцию связности - Тулио Леви-Чивита.


Спасибо ! 
Ваш ответ прояснил мне смысл понятия связности как того, посредством чего задается дифференцирование сечений лок. трив. расслоения.

Ваш ответ прояснил мне смысл понятия связности как того, посредством чего задается дифференцирование сечений лок. трив. расслоения.
пока вопросов нет, развлекательный ликбез.. великий российский геометр, специалист в дифференциальной геометрии Григорий Перельман. Отказался от Филдсовской медали по неизвестным причинам.


может, я чего-то не догоняю в принципе. Как я понял, форма объема в Минковском все же может быть построена.
Что радует. Свертка вект.поля с нормалью меняет лишь знак слагаемых, а не что-то концептуально.
Тогда практический вопрос: Можно ли (и как, если можно) определить поток от Т^{\mu\nu} (или от векторного поля A^{\nu}, если в Т зафиксировать мю)
1) через пространственноподобную гиперповерхность
2) через светоподобную гиперповерхность
например, по свет.конусу (можно с исключенной вершиной напр. в будущее (2) и его крышке (1)
Например (если можно в обоих случаях) для определенности, если свет.конус с вершиной в точке x есть C={x'|(x-x')^2=0}, то "нормаль" (точнее, ненормируемая "ортогональ") к С будет состоять из касательного же вектора (x-x'). Если векторное поле имеет вид A^{\nu}=B*(x-x')^{\nu} — то понятно, что при любом определении будет ноль в свертке. Интересует поток для произвольного (гладкого) поля A^{\nu}
Что тогда с чем нужно сворачивать?
Что радует. Свертка вект.поля с нормалью меняет лишь знак слагаемых, а не что-то концептуально.
Тогда практический вопрос: Можно ли (и как, если можно) определить поток от Т^{\mu\nu} (или от векторного поля A^{\nu}, если в Т зафиксировать мю)
1) через пространственноподобную гиперповерхность
2) через светоподобную гиперповерхность
например, по свет.конусу (можно с исключенной вершиной напр. в будущее (2) и его крышке (1)
Например (если можно в обоих случаях) для определенности, если свет.конус с вершиной в точке x есть C={x'|(x-x')^2=0}, то "нормаль" (точнее, ненормируемая "ортогональ") к С будет состоять из касательного же вектора (x-x'). Если векторное поле имеет вид A^{\nu}=B*(x-x')^{\nu} — то понятно, что при любом определении будет ноль в свертке. Интересует поток для произвольного (гладкого) поля A^{\nu}
Что тогда с чем нужно сворачивать?
Дело вот в чем. В евклидовом случае элемент обьема определяется любой четверкой ортонормальных векторов и любое векторное поле можно свернуть с элементом обьема, используя скалярное произведение с нормалью, какой бы эта нормаль не была. Это обеспечивается транзитивностью действия группы на пространстве всех направлений. Иными словами, имея нормаль в данной точке, можно легко найти элемент обьема, содержащий эту нормаль. И свертку векторного поля с этим элементом обьема можно выразить через скалярное произведение вектора с нормалью ( а можно и не выражать, а просто свернуть).
В псевдоевклидовом случае элемент обьема просто совпадает с евклидовым ( как будто метрики Минковского нет и в помине). Поэтому векторное поле можно что просто сворачивать с элементом обьема, либо тоже самое выражать через скалярное произведение с евклидовой ( а не псевдоевклидовой нормалью).
То есть суть в том, что псевдометрику ввести можно, но вот псевдообьем концептуально отличаться от обьема не будет..
Скалярное произведение с нормалью - это лишь способ выразить свертку векторного поля с элементом обьема, который что в евклидовом, что в псевдоевклидовом случае один и тот же.
В псевдоевклидовом случае элемент обьема просто совпадает с евклидовым ( как будто метрики Минковского нет и в помине). Поэтому векторное поле можно что просто сворачивать с элементом обьема, либо тоже самое выражать через скалярное произведение с евклидовой ( а не псевдоевклидовой нормалью).
То есть суть в том, что псевдометрику ввести можно, но вот псевдообьем концептуально отличаться от обьема не будет..
Скалярное произведение с нормалью - это лишь способ выразить свертку векторного поля с элементом обьема, который что в евклидовом, что в псевдоевклидовом случае один и тот же.
Поскольку прозвучал вопрос по теории струн.. небольшой развлекательный ликбез. Один из ведущих в мире специалистов по теории струн Лиза Рэндалл.


Поскольку прозвучал вопрос по теории струн.. небольшой развлекательный ликбез. Один из ведущих в мире специалистов по теории струн Лиза Рэндалл.Рэндалл вроде как не является специалистом в струнах, а известна большей частью по работам о braneworlds и космологии. К струнам относить всех подряд конечно можно, но нежелательно.
вроде как не является специалистом в струнахНу хорошо, для тех кому нужен настоящий специалист, развлекательный ликбез.. один из ведущих в мире специалистов по теории струн, Филдсовский лауреат Эдвард Виттен

не является специалистом в струнах, а известна большей частью по работам о braneworldsа браны это типа не многомерные струны
Пока вопросы иссякли, немного классики.. Карл Фридрих Гаусс
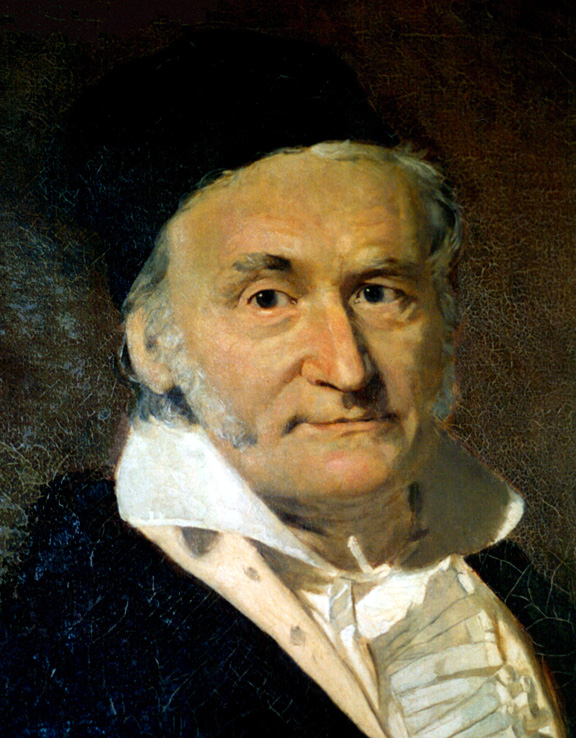
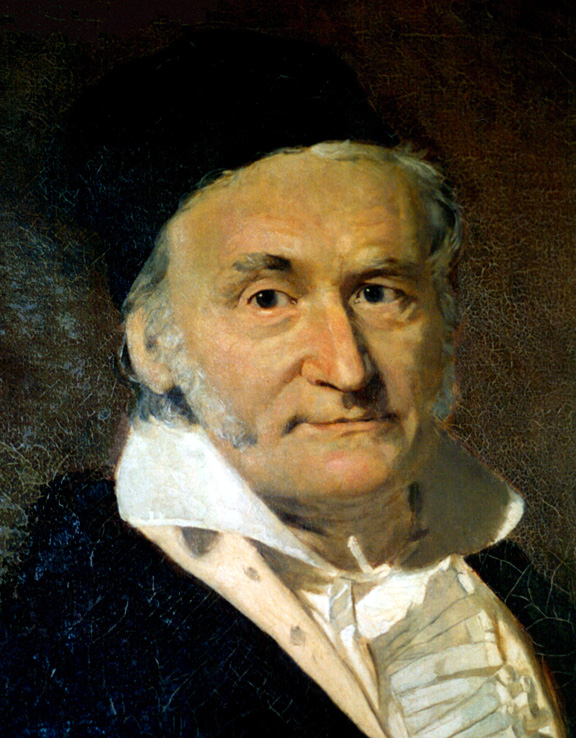
Заметьте какой проницательный, глубокий взгляд у людей на всех фотографиях. Разгадка проста - математика сильно развила интеллект этих людей, то есть то, чем человек отличается от обезьяны.
И напоследок перед отьездом.. гордость мехмата, один из ведущих специалистов мира по теории струн, Филдсовский лауреат Максим Концевич


гордость мехмата,Элементов всех таблицу
Кто увидел в страшном сне?
Кем Россия вся гордится,
А евреи — так вдвойне? /И.Иртеньев/
А с чего это мехмат им гордится? Он что, на нем работает?
А с чего это мехмат им гордится?ну я искренне теряюсь что ответить на этот вопрос, поэтому оставлю без ответа.
У человека со стороны может возникнуть естественный вопрос - тред посвящен дифференциальной геометрии, а постятся фотки учОных из теории струн..
Все просто -эти две науки очень глубоко пересекаются и можно сказать в первом приближении совпадают.
Все просто -эти две науки очень глубоко пересекаются и можно сказать в первом приближении совпадают.
немного ликбеза.. один из центральных дифференциально-геометрических обьектов современной теоретической физики, многообразие Калаби-Яу.
Предполагается, что эта многомерная поверхность имеет непосредственное отношение к структуре нашего с Вами пространства..

Предполагается, что эта многомерная поверхность имеет непосредственное отношение к структуре нашего с Вами пространства..

Отказался от Филдсовской медали по неизвестным причинам.вроде ему две филдсовских медали присуждали - нет?
нет, две филдсовских никогда никому не присуждали, Перельману готовы дать приз института Клэя - миллион долларов, но он не очень заинтересован и в принципе я могу понять почему
Немного классики, Бернгард Риман


Меня уже несколько человек с разных факультетов в привате спросили, как улучшить свои навыки в математике или просто развить математическое мышление..
Я рекомендую для начального уровня решать задачи из задачника Демидовича
Я рекомендую для начального уровня решать задачи из задачника Демидовича
а что делать дальше? когда все прорешаны и не вызывают трудностей?
пояснишь, почему? //правда, интересно:)
Я рекомендую для начального уровня решать задачи из задачника ДемидовичаЭто хороший совет, но немного школярский, если честно.
Я рекомендую тем, кто еще в МГУ или в окрестностях, у кого есть время и кому это
нужно/интересно, просто ходить на мехмат и слушать там любые лекционные курсы
на свой вкус. Благо, пускают бесплатно, и фэйс-контроль не устраивают.
Про эту возможность Lin в параллельном треде как раз говорила.
Потом можно походить и на спецкурсы, и на спецсеминары, пообщаться с людьми.
Не только на мехмат, к другим факультетам это тоже относится.
Лекции слушать - дело хорошее, но, в основном, лишь для расширения кругозора. Без хотя бы какой-то практики далеко не уйдешь.
Практика подразумевается.
В смысле - если у человека не просто интерес ко всему интересному,
а конкретный запрос. Те-то и те-то методы нужны в его области. Идет,
осваивает, применяет.
А если и просто интерес - без практики - тоже ничего плохого, математика
вполне самодостаточная дисциплина, ум дисциплинирует, всё такое...
А дальше уж как сложится.
ЗЫ Лично знаком с выпускниками других факультетов МГУ, которые занялись
впоследствие математикой - просто начали ходить, а потом понравилось...
В смысле - если у человека не просто интерес ко всему интересному,
а конкретный запрос. Те-то и те-то методы нужны в его области. Идет,
осваивает, применяет.
А если и просто интерес - без практики - тоже ничего плохого, математика
вполне самодостаточная дисциплина, ум дисциплинирует, всё такое...
А дальше уж как сложится.
ЗЫ Лично знаком с выпускниками других факультетов МГУ, которые занялись
впоследствие математикой - просто начали ходить, а потом понравилось...
>Практика подразумевается.
>В смысле - если у человека не просто интерес ко всему интересному,
>а конкретный запрос. Те-то и те-то методы нужны в его области. Идет,
>осваивает, применяет.
Это не совсем та практика, которую я имел в виду.
Для понимания лекционного курса обычно требуется
способность более-менее свободно оперировать с теми
математическими объектами, которые рассматриваются
в курсе. Для развития этой способности требуется
решать небольшие модельные задачи, например, задачи
из "демидовича".
Без решения задач прослушивание курса даст лишь
представление о том, чем занимаются в той
или иной области.
>В смысле - если у человека не просто интерес ко всему интересному,
>а конкретный запрос. Те-то и те-то методы нужны в его области. Идет,
>осваивает, применяет.
Это не совсем та практика, которую я имел в виду.
Для понимания лекционного курса обычно требуется
способность более-менее свободно оперировать с теми
математическими объектами, которые рассматриваются
в курсе. Для развития этой способности требуется
решать небольшие модельные задачи, например, задачи
из "демидовича".
Без решения задач прослушивание курса даст лишь
представление о том, чем занимаются в той
или иной области.
Ну все зависит от базового уровня, конечно.
Кому-то и с Демидовича надо начать.
А на естественных факультетах, где
студенты проходят анализ хоть в каком-то
объеме, дифференцировать-интегрировать
мало-мальски учат. Это как бы базовый ликбез.
Дальше, если человек ликбез освоил, и его
интересуют уже какие-то более продвинутые курсы,
он может и сам решить, в каком объеме ему что
нужно/интересно. Необязательно, чтобы тебя именно
вызывали к доске и заставляли что-то решать.
Пишу и вспоминаю - однажды уже была эта тема...
Кажется, про психологию с кем-то говорил, примерно
в том же ключе.
Кому-то и с Демидовича надо начать.
А на естественных факультетах, где
студенты проходят анализ хоть в каком-то
объеме, дифференцировать-интегрировать
мало-мальски учат. Это как бы базовый ликбез.
Дальше, если человек ликбез освоил, и его
интересуют уже какие-то более продвинутые курсы,
он может и сам решить, в каком объеме ему что
нужно/интересно. Необязательно, чтобы тебя именно
вызывали к доске и заставляли что-то решать.
Пишу и вспоминаю - однажды уже была эта тема...
Кажется, про психологию с кем-то говорил, примерно
в том же ключе.
Дело вовсе не в уровне и даже не в "демидовиче".
Я отвечал на конкретное предложение:
>Я рекомендую тем, кто еще в МГУ или в окрестностях, у кого есть время и кому это
>нужно/интересно, просто ходить на мехмат и слушать там любые лекционные курсы
>на свой вкус. [...]
>
>Потом можно походить и на спецкурсы, и на спецсеминары, пообщаться с людьми.
Тут предлагается просто ходить и слушать/смотреть.
Я говорю, что этого не достаточно. Нужно еще решать
модельные задачи по тематике курсов, чтобы
на собственном опыте почувствовать, о чем речь.
P.S. Думаю, вы это понимали, просто не озвучили
Я отвечал на конкретное предложение:
>Я рекомендую тем, кто еще в МГУ или в окрестностях, у кого есть время и кому это
>нужно/интересно, просто ходить на мехмат и слушать там любые лекционные курсы
>на свой вкус. [...]
>
>Потом можно походить и на спецкурсы, и на спецсеминары, пообщаться с людьми.
Тут предлагается просто ходить и слушать/смотреть.
Я говорю, что этого не достаточно. Нужно еще решать
модельные задачи по тематике курсов, чтобы
на собственном опыте почувствовать, о чем речь.
P.S. Думаю, вы это понимали, просто не озвучили

Ок 

Нужно еще решатьЕсть книжка Пойа Д. Математика и правдоподобные рассуждения
модельные задачи по тематике курсов, чтобы
на собственном опыте почувствовать, о чем речь.
Там есть такие вещи, которых на мехмате не рассказывают. Когда я прочитал, то был сильно удивлён.
Самое интересное, там показаны такие идеи, с помощью которых, возможно, великие математики прошлого делали свои открытия. Понимание таких идей позволяет почувствовать, что такое математическое мышление.
Ещё есть книга с задачками для решения в уме, типа там задачки-пятиминутки, и автор пишет в предисловии, что вся фишка - решить задачу не пользуясь ручкой и бумагой, иначе слишком просто. Книга не требует начальной подготовки, офигенно подходит для решения задач в метро и здорово развивает мозг.
К сожалению, не могу вспомнить название этой книги, но почему-то мне кажется, что верно хотя бы одно из следующего:
1) Автор - Льюис Кэрролл
2) книга выходила в серии "Библиотека КВАНТ".
Под эти условия подходит "Логическая игра", но это точно не оно. Может быть, эта книга - "История с узелками" Кэрролла. Если нет, значит я что-то напутал.
Но книга такая точно была

Вернулся, задавайте вопросы
Может и был такой вопрос... Что по Вашему мнению является самым главным достижением в этой области науки и почему? Конечно понимаю, что выделять что-то одно не совсем корректно, но всё же интересен ответ на этот вопрос...
Ну.. по моему мнению фантастическим достижением является не какой-то конкретный результат, а постепенное ' результативное' слияние с физикой высоких энергий и просто с физикой.
Раньше математика помогала решать физические задачи, а сейчас происходит наоборот и это по-настоящему круто.
Например очень технически сложные работы Дональдсона по 'ложному R^4' ( многообразие гомеоморфное, но не диффеоморфное R^4) были проинтерпретированы и сильно прояснены Виттеном в терминах магнитного монополя.
Очень глубокая, и еще не доказанная 'гипотеза о зеркальной симметрии' пришла в математику из некоторых моделей теории суперструн.
Недавний результат Перельмана основан на изучении свойств потока Риччи для тензора кривизны, который по сути описывается аналогом уравнения теплопроводности для кривизны, то есть основан на аналогии кривизна-тепло. ( Если изогнуть железную балку, то сильнее всего она нагреется в месте изгиба)
Так же я слышал краем уха, что некие физические соображения позволяют ' начинать подбираться' к ВТ Ферма, хотя объективно это пока только мечты. Но, конечно, я бы очень хотел застать тот день когда ВТФ будет доказана ' физически'.
Раньше математика помогала решать физические задачи, а сейчас происходит наоборот и это по-настоящему круто.
Например очень технически сложные работы Дональдсона по 'ложному R^4' ( многообразие гомеоморфное, но не диффеоморфное R^4) были проинтерпретированы и сильно прояснены Виттеном в терминах магнитного монополя.
Очень глубокая, и еще не доказанная 'гипотеза о зеркальной симметрии' пришла в математику из некоторых моделей теории суперструн.
Недавний результат Перельмана основан на изучении свойств потока Риччи для тензора кривизны, который по сути описывается аналогом уравнения теплопроводности для кривизны, то есть основан на аналогии кривизна-тепло. ( Если изогнуть железную балку, то сильнее всего она нагреется в месте изгиба)
Так же я слышал краем уха, что некие физические соображения позволяют ' начинать подбираться' к ВТ Ферма, хотя объективно это пока только мечты. Но, конечно, я бы очень хотел застать тот день когда ВТФ будет доказана ' физически'.
немного развлекательного ликбеза..
Один из ведущих российских специалистов по дифференциальной геометрии, историк, и, добавлю от себя, замечательный лектор, академик РАН Анатолий Тимофеевич Фоменко.

Один из ведущих российских специалистов по дифференциальной геометрии, историк, и, добавлю от себя, замечательный лектор, академик РАН Анатолий Тимофеевич Фоменко.

Предлагаю переименовать тред в
"Популярно о том, чего вы так боялись" (для ММ или "Популярно о том, о чем сложно даже спросить".
"Популярно о том, чего вы так боялись" (для ММ или "Популярно о том, о чем сложно даже спросить".
пока вопросов нет, продолжаем классику.. Грегорио Риччи.. основатель важнейшего дифф.геометрического понятия - тензора Риччи


искренняя рекомендация студентам и аспирантам мехмата - друзья, если в будущей своей карьере хотите быть в математическом мейнстриме, то не затягивайте с изучением алгебраической геометрии . лучше поздно, чем никогда.
я в свое время забил, сейчас приходится полуаврально наверстывать.
я в свое время забил, сейчас приходится полуаврально наверстывать.
Грегорио РиччиЗапости плиз краткую биографию для безынетных вроде меня.
А что в тензоре Риччи "важнейшего" и того, что "можно было основывать"? Я не знаю хронологию открытий — но сейчас (в учебниках) тензор Риччи — не более, чем свертка тензора кривизны (Римана)?
Запости плиз краткую биографиюГрегорио Риччи-Курбастро (итал. Gregorio Ricci-Curbastro; 12 января 1853, Луго — 6 августа 1925, Болонья) — итальянский математик.
С 1880 г. — профессор в университете в Падуе. Его важная научная заслуга заключается в создании «абсолютного дифференциального исчисления» (тензорного исчисления)..
больше ничего особо не нашел..

я попробую пояснить..
В математике важность какой-либо концепции обьекта НЕ ВСЕГДА пропорциональна сложности его построения.
Пример - есть весьма сложно определяемая и нудная конструкция так называемого интеграла Курцвейля-Хенстока. Чтобы просто дать определение этого интеграла и доказать его простейшие свойства ( типа аддитивности нужно потратить приличные усилия.
А есть такое простейшее понятие, как собственное значение матрицы.
В итоге имеем, что интеграл Курцвейля-Хенстока нужен тока специалистам в нем ( ибо в математике все функции либо гладкие, либо интегрируются по Лебегу а про собственные значения матрицы разговор излишен.
Касательно тензора Риччи - это очень удобный обьект.. именно эволюцию этого тензора исследовал Перельман в док-ве гипотезы Пуанкаре.
В математике важность какой-либо концепции обьекта НЕ ВСЕГДА пропорциональна сложности его построения.
Пример - есть весьма сложно определяемая и нудная конструкция так называемого интеграла Курцвейля-Хенстока. Чтобы просто дать определение этого интеграла и доказать его простейшие свойства ( типа аддитивности нужно потратить приличные усилия.
А есть такое простейшее понятие, как собственное значение матрицы.
В итоге имеем, что интеграл Курцвейля-Хенстока нужен тока специалистам в нем ( ибо в математике все функции либо гладкие, либо интегрируются по Лебегу а про собственные значения матрицы разговор излишен.
Касательно тензора Риччи - это очень удобный обьект.. именно эволюцию этого тензора исследовал Перельман в док-ве гипотезы Пуанкаре.
А ещё уравнения Эйнштейна через него записываются, если не путаю ничего.
Однако и я не могу ответить на вопрос - "а что дал тебе тензор Риччи?" Мне как будто бы ничего. Можно ещё пояснений на тему важности и полезности этого объекта в народном хозяйстве?
Однако и я не могу ответить на вопрос - "а что дал тебе тензор Риччи?" Мне как будто бы ничего. Можно ещё пояснений на тему важности и полезности этого объекта в народном хозяйстве?

а еще, например, такоей фундаментальный объект современной математики и физики как многообразие Калаби-Яу обладает нулевым тензором Риччи, причем это свойство заложено в его определение.
Я думаю, хотя бы эти три причины ( док-во гипотезы Пуанкаре, уравнения Эйнштейна, многообразие Калаби-Яу) как то оправдывают введение тензора Риччи?
Я думаю, хотя бы эти три причины ( док-во гипотезы Пуанкаре, уравнения Эйнштейна, многообразие Калаби-Яу) как то оправдывают введение тензора Риччи?

Объективный толк от доказательства (уже теперь) теоремы Пуанкаре мне кажется сомнительным, хотя я не геометр конечно. Имхо гипотеза Римана (о нулях дзета-функции) куда полезнее: на неё хоть криптография завязана. А на теорему Пуанкаре - что завязано? Я не знаю. Расскажи плиз, если знаешь?
Уравнения Эйнштейна - ну наверное они полезны. Наверное. Космологи наверное плакать будут, если вдруг уравнения Эйнштейна запретят писать. Но вот ОТО и СТО вроде как можно и без них ввести, так что зачем они простому смертному? Я не знаю. Расскажешь?
Многообразия Калаби-Яу - тоже хз на самом деле, что из них выйдет. Сейчас это модно, а что будет через 50 лет - время покажет. Спорить о теории струн - смысла нет, потому что её полезность хотя бы в том, что она привлекает талантливых людей заниматься наукой, а не чем-то другим, потому что очень уж амбициозна. Что, правда теория струн без тензора Риччи совсем-совсем никак не может, да?
Прошу понять мой пост правильно: это не критика или спор, нет, я просто спрашиваю, прошу пояснить. Ты же обещал отвечать на вопросы по ДГ в этом треде
Уравнения Эйнштейна - ну наверное они полезны. Наверное. Космологи наверное плакать будут, если вдруг уравнения Эйнштейна запретят писать. Но вот ОТО и СТО вроде как можно и без них ввести, так что зачем они простому смертному? Я не знаю. Расскажешь?
Многообразия Калаби-Яу - тоже хз на самом деле, что из них выйдет. Сейчас это модно, а что будет через 50 лет - время покажет. Спорить о теории струн - смысла нет, потому что её полезность хотя бы в том, что она привлекает талантливых людей заниматься наукой, а не чем-то другим, потому что очень уж амбициозна. Что, правда теория струн без тензора Риччи совсем-совсем никак не может, да?
Прошу понять мой пост правильно: это не критика или спор, нет, я просто спрашиваю, прошу пояснить. Ты же обещал отвечать на вопросы по ДГ в этом треде

ну это вопросы по сути из серии " нужна ли домохозяйкам ВТФ ?" . Не нужна, но who cares..

искренняя рекомендация студентам и аспирантам мехмата - друзья, если в будущей своей карьере хотите быть в математическом мейнстриме, то не затягивайте с изучением алгебраической геометрии . лучше поздно, чем никогда.По какой литературе посоветуешь изучать?
я в свое время забил, сейчас приходится полуаврально наверстывать.
Для таких как я, НЕспециалистов в алгебраической геометрии, но кому необходимо хорошее ее знание ( ибо она используется очень много где рекоммендовал бы хорошо написанные книжки:
1) David Mumford " Algebraic geometry"
2) David Eisenbud, Joe Harris " The Geometry of Schemes"
3) Gunter Tamme " Introduction to Etale Cohomology"
Там нет глубокого погружения в узкоспециальные аспекты, интересные лишь специалистам, но в то же время дают общее хорошее представление о предмете.
1) David Mumford " Algebraic geometry"
2) David Eisenbud, Joe Harris " The Geometry of Schemes"
3) Gunter Tamme " Introduction to Etale Cohomology"
Там нет глубокого погружения в узкоспециальные аспекты, интересные лишь специалистам, но в то же время дают общее хорошее представление о предмете.
Короткий вопрос.
Откуда взялось и как доказать равенство для символов леви чивиты .....
заранее спасибо!
http://upload.wikimedia.org/math/4/2/1/421a37e6d8c1feb69dc10...
Откуда взялось и как доказать равенство для символов леви чивиты .....
заранее спасибо!
http://upload.wikimedia.org/math/4/2/1/421a37e6d8c1feb69dc10...
это координатное представление одной тензорной операции - так называемой 'звездочки Ходжа'. Сейчас занят, подробнее напишу попозже
нет глубокого погруженияВот про погружение вопрос:допустим, оно есть (многообразия буду называть "поверхность" — вложенное и "пространство" — объемлющее, координаты латинские для пов. и греч. — для пр-ва тогда ур-я Вайнгартена
— это просто определения соответствующих сверток в терминах объемлющего ск.произведения (обозначаемого просто точкой)
В то же время если отвлечься от погружения и посчитать внутренние символы Кристоффеля
и выписать $h_{ab}$ как индуцированную метрику
то получится
Если же расписать ковариантную производную D от $\partial_{a}z$ то получится
,т.е. симметричное по $a$ и $b$ выражение (cd-во *т.е. $z^{\mu}$ ведет седя вдоль поверхности как скаляр)отсюда получается сразу
—а это определение
Это же получается просто из свойства (* если пытаться создать трехиндекную $\gamma_{abс}$, симметричную по первой паре и антисимметричную по второму и третьему индексам
Вопрос: если нет нигде у меня ошибки — нафига пишут связность $\gamma_{abс}$. Если есть ош. — то где?
спасибо за вопрос. седня у меня сильно занятой день, я чуть позже выкрою время и отвечу
to
прочитал и вообще ничего не понял.
 не привыкну я к твоему стилю изложения никак. так что дай мне время понять, что написано
не привыкну я к твоему стилю изложения никак. так что дай мне время понять, что написано 
прочитал и вообще ничего не понял.

 не привыкну я к твоему стилю изложения никак. так что дай мне время понять, что написано
не привыкну я к твоему стилю изложения никак. так что дай мне время понять, что написано 
Короткий вопрос.сначала откуда взялось.
Откуда взялось и как доказать равенство для символов леви чивиты .....
заранее спасибо!
http://upload.wikimedia.org/math/4/2/1/421a37e6d8c1feb69dc10...
для пространства со скалярным произведением, как известно, пространство естественно отождествляется с сопряженным. Оказывается, это же отождествление можно естественным образом продолжить и на все внешние степени. То есть каждую k-форму можно представить как формальную линейную комбинацию нескольких k-плоскостей, а действие этой k-формы на набор из k векторов (k-параллелограм) как взвешенную сумму площадей проекций этого параллелограма на заданные k-плоскости. Это основы так называемой теории Ходжа.
Символ Леви-Чивита это не что иное как коэффициенты кососимметрической n-формы в ортогональном базисе. Естественно он кососимметричен, ведь при перестрановке любых двух векторов базиса форма поменяет знак.
Теперь как доказать формулу. Выражения слева и справа кососимметричны по индексам (i,j,k) и (l,n,m значит их можно перестановками индексов можно привести к виду (1,2,3) (1,2,3).. тем самым матрица справа станет единичной, что и докажет формулу.
Возможно не все понятно рассказал, задавай вопросы если что.
Первая формула (Вайнгартен) — это просто разложение ков.производной по базису {е_a; n_j} где e — касательный ортонормированный базис, n — ортоноримрованный базис "дополнения" в каждой точке.
Если метрика индуцированная — то касательные вектора будут $e_a=\partial_a z^{\mu}$.
Вопрос заключается в том, почему у меня при индуцированной метрике получается тождественный ноль для связностей $\gamma_{abc}$ (которые определяются как $\gamma_{abc}=D_a e_b \cdot e_c$ )?
Если метрика индуцированная — то касательные вектора будут $e_a=\partial_a z^{\mu}$.
Вопрос заключается в том, почему у меня при индуцированной метрике получается тождественный ноль для связностей $\gamma_{abc}$ (которые определяются как $\gamma_{abc}=D_a e_b \cdot e_c$ )?
ага, ок, попозже отвечу. я щас на работу подаюсь и рассылаю аппликации, времени мало
отвлечься от погруженияя не проверял твои выкладки досконально, но это первое что бросилось в глаза. В уравнениях Вайнгартена нельзя отвлечься от погружения. Они описывают так называемую внешнюю кривизну, которая НЕ является внутренним инвариантом поверхности, а зависит от того, как именно поверхность вложена в обьемлющее пространство.
Кстати по этому поводу вот вспомнилось.
Однажды мне заметили, что хаусдорфова (она же фрактальная) размерность тоже никак не описывает топологию самого пространства, а описывает способ его вложения в![[math]$\mathbb{R}^n$ [/math]](mathimg.php?math=%24%5Cmathbb%7BR%7D%5En%24%20) .
.
То есть топология, например, на острове Коха - это стандартная топология окружности.
Однажды мне заметили, что хаусдорфова (она же фрактальная) размерность тоже никак не описывает топологию самого пространства, а описывает способ его вложения в
То есть топология, например, на острове Коха - это стандартная топология окружности.
хочу немного пофилософствовать. заметил, что многие глубокие матем. результаты, где так или иначе фигурирует понятие гладкости, ну там гладкая функция или диффеоморфизм итд. используют от этой самой гладкости по сути только правило Лейбница d(fg)=d(f)g+fd(g ну то есть просто концепцию алгебры с дифференцированием.
в общем почему то кажется что анализ как таковой отмирает, то есть в будущем 'выживут' только алгебраизируемые обьекты, а всякие гладкие, обобщенные функции, ряды Фурье, Тейлора, разбиения единицы отойдут в раздел " история математики".
в общем почему то кажется что анализ как таковой отмирает, то есть в будущем 'выживут' только алгебраизируемые обьекты, а всякие гладкие, обобщенные функции, ряды Фурье, Тейлора, разбиения единицы отойдут в раздел " история математики".
в общем почему то кажется что анализ как таковой отмирает, то есть в будущем 'выживут' только алгебраизируемые обьекты,Если принять концепцию Вербицкого, то есть "нет математики кроме алгебраической геометрии" - то может и так, судить не возьмусь, ибо не специалист в АГ.
Если же не зашориваться до такой степени, то я уверен, что ты ошибаешься. Ряды Тейлора никак не выкинешь из численных методов вычислений, преобразование Фурье вовсю использует инжереная физика и от спектров частот сигнала она не откажется ну никак, гладкие функции нужны для рядов Тейлора, ну и так далее.
Разве что вот насчёт обобщённых функций я х.з. Понятие это неоднозначное, потому что ясное дело они многое дают, но есть с ними проблемы (например, проблема умножения). Несомненно, что какие-то примитивные обобщённые функции, глубоко вошедшие в культуру, типа Дельта Дирака как плотность массы материальной точки, ясное дело, не исчезнут. А вот теория обобщённых функций вообще, может быть, и сменится со временем чем-то более удачным.
В любом случаем, я бы не стал ограничиваться поклонением только одной ветви математики - алгебра будь то или анализ, или геометрия, или, например, компьютерная математика. Математика едина, и она не раз доказывала людям это.
Всё написанное выше - моё имхо.
Так я и не отвлекался: с одной стороны сравнивал ур-я Вайгартена (где фигурировали связности $\gamma$ и внешняя кривизна К а с другой — рассматривал чисто вложенную поверхность КАК НЕЗАВИСИМОЕ ПРОСТРАНСТВО С МЕТРИКОЙ, ИНДУЦИРОВАННОЙ из объемлющего (после чего забываю, откуда метрика пришла и рассматриваю ее независимо, как "богом данное нам в ощущениях" т.е. рассматривал конкретное, фиксированное вложение. И в нем считал Кристоффели $\Gamma$ и т.д. внутренним образом, по известным формулам (лучше даже не представлять это в терминах скал.пр-ия внешнего пр-ва, даже если оно естественным образом получается). Т.е. Вайнгартен тут уже не при чем. [Можно ли это делать? — я считаю, почему нет!, например, если вычислять кривизны шара по его индуцированной метрике, вложенного в плоское пр-во, мы можем независимо это делать]
Но поскольку я двумя способами выражал одно и то же (вторые производные я их и приравниваю и из симметрий получается то, что получается. Получается странно — но я пока не вижу явной ошибки
Но поскольку я двумя способами выражал одно и то же (вторые производные я их и приравниваю и из симметрий получается то, что получается. Получается странно — но я пока не вижу явной ошибки
вычислять кривизны шара по его индуцированной метрике, вложенного в плоское пр-во, мы можем независимо это делатьА вот такие вот вещи не смущают?
Между прочим, если верить тому, что пишет Арнольд в одной научно-популярной брошюрке, Лейбниц изначально допустил ошибку, написав, что d(f*g)=df*dg, т.е. что d - гомоморфизм. Причина его ошибки была как раз в том, что он рассуждал именно как отвлеченный алгебраист, но не как "эмпирик" типа Ньютона. Ньютон рассмотрел бы приращение площади прямоугольника со сторонами f и g при бесконечно малых приращениях длин этих сторон, и получил бы правильный результат, состоящий из площадей двух узких полосок f*dg+g*df, а величиной df*dg , несомненно, пренебрег бы. Мораль в том, что чрезмерное увлечение формально-алгебраическими построениями, т.е. бурбакизация, чревато потерей непосредственного (здравого) смысла.
чрезмерное увлечение формально-алгебраическими построениями, т.е. бурбакизация, чревато потерей непосредственного (здравого) смысла.+1
(офф-топ: ну, вообще-то, имхо, формализация теории множеств порождает много аналогичных проблем, типа тех, которые мы обсуждали недавно). Удивительно другое, что даже сами геометры стремятся к отказу от чертежей, если образно выражаться. Мэйнстрим?
да, я тебя понял.. хм, я подумаю. я не задумывался над таким, но вопрос понятен.
А вот такие вот вещи не смущают?он рассматривает индуцированную метрику, а она уже учитывает способ погружения по определению. Тут встает вопрос, достаточно ли знания индуцированной метрики, чтобы восстановить вложение, с точностью до ортогональных преобразований.
Вопрос интересный, я никогда не задумывался, но думаю он легко выясняется. Я чуть с делами разберусь и отвечу.
чревато потерей непосредственного (здравого) смысла.по такой логике ( опираться на 'здравый' смысл) не было бы теории относительности, квантовой механики и много еще чего.
Вопрос интересный, я никогда не задумывался, но думаю он легко выясняется. Я чуть с делами разберусь и отвечу.Спасибо

по такой логике ( опираться на 'здравый' смысл) не было бы теории относительности, квантовой механики и много еще чего.Не, он говорит о том, что ЧЕРЕСЧУР отказываться от зравого смысла и верить в алгебру одну лишь великую - плохо, потому что ошибки детектировать сложно, если не видишь геометрических образов хоть каких-то за формулами. Так-то понятно, что математика - вещь абстрактная, кто ж спорить будет.
достаточно ли знания индуцированной метрики, чтобы восстановить вложение, с точностью до ортогональных преобразований.а этого НЕдостаточно, например у обычной кривой в R^3, кроме кривизны есть еще и кручение, которое в определенном смысле независимо, от внутренне метрике. Все, скоро детально рассмотрю выкладки силиконца и найду ошибку.

даже сами геометры стремятся к отказу от чертежей, если образно выражаться.Не уверен, что это так.
Что скажут сами геометры?
все, я тут сам с собой рассуждая, придумал модельный пример - нужно рассмотреть кусок плоскости ( линейно вложенный в R^3) и кусок цилиндра. Индуцированная метрика будет одна и та же, поведение нормалей очевидно разное. Напишу в деталях позже.
Поскольку я сам занимаюсь всякими приложениями квантов, я не считаю кванты противоречащими здравому смыслу.  А вообще, мысль у Арнольда про другое была.
А вообще, мысль у Арнольда про другое была.
 А вообще, мысль у Арнольда про другое была.
А вообще, мысль у Арнольда про другое была.мысль у Арнольда про другое была.Ну, мое резюме мыслей Арнольда ( по результатам его многочисленных выступлений в разных местах ) : " взять бы всех Бурбаков да на Колыму"

Меня позабавила его классификация "право-" и "левополушарных" математиков. Наверное, в этом что-то есть.
Ну, мое резюме мыслей Арнольда ( по результатам его многочисленных выступлений в разных местах ) : " взять бы всех Бурбаков да на Колыму"http://www.mccme.ru/edu/index.php?ikey=viarn_burbaki
ВЕСТНИК РОССИЙСКОЙ АКАДЕМИИ НАУК
том 72, N 3, с. 245-250 (2002)
© В.И. Арнольд
Материал скопирован с сайта Vivos Voco
МАТЕМАТИЧЕСКАЯ ДУЭЛЬ ВОКРУГ БУРБАКИ
В. И. Арнольд
Арнольд Владимир Игоревич - академик, гл. н. с.
Математического института им. В.А. Стеклова РАН.
На дуэль меня вызвал Ж.-П. Серр, мотивировавший свой вызов так: "Я хочу рассказать о влиянии Бурбаки на математику. Но если все будут говорить одно и то же, да еще панегирически, то это будет скучно. Поэтому я стал искать, кто бы мог высказать наиболее противоположное моему мнение. И, перелистав справочник математиков мира, понял, что это ты".
Дуэль состоялась 13 марта 2001 г. в Институте А. Пуанкаре. Каждый из нас говорил по часу. В заключительном слове Серр сказал: "Теперь мы еще раз убедились, какая это замечательная наука - математика. Люди со столь противоположными мнениями, как мы двое, могут в ней сотрудничать, уважать друг друга, знать и использовать результаты друг друга, сохраняя при этом свои противоположные мнения... И, смотрите - мы оба остались живы...". Ниже я постараюсь описать эту дискуссию.
Первым выступил Серр. Он рассказал об основных достижениях Бурбаки и его школы. Поскольку очень многое из этого хорошо известно, я остановлюсь только на том, что меня особенно поразило в выступлении Серра.
Прежде всего - об особенной роли нуля. Оказывается, нуль - положительное число. Действительно, для Бурбаки все общие понятия важнее их частных случаев, поэтому все нестрогие неравенства являются фундаментальными, а строгие - маловажными специальными случаями, примерами. В соответствии с этим во Франции слово "больше" в математике означает то, что мы называем "больше или равно". Например, каждое вещественное число больше самого себя, а значит, нуль больше нуля и, следовательно, положителен!
По этому поводу я прочел в инструкции для студентов первого курса Парижского университета Орсэ: "В англо-саксонских учебниках, которые (к сожалению? - В. А.) еще сохранились в библиотеке, вы можете встретить другую точку зрения на неравенства, что особенно неприятно при работе с e-d-определениями в теории непрерывности и пределов, в частности, при попытках сформулировать отрицание сходимости. Но не забывайте, что вы учитесь во Франции, и поэтому пользование англо-саксонскими неравенствами может сильно повредить вам на экзаменах". Мои французские коллеги сказали мне, что они считают русские книги "англо-саксонскими". Впрочем, в русских книгах "встречаются и своеобразные другие нелепости": в них "линейными пространствами" называются многомерные векторные пространства, в то время как всякому известно, что слово "линейный" означает "одномерный" (как линия). С тех пор "линейное пространство" я стал везде заменять "векторным", хотя и не смог заставить себя считать нуль положительным числом.
Кроме положительности нуля, то же рассуждение устанавливает и его отрицательность (ибо нуль меньше нуля по французско-бурбакистской терминологии). Мои коллеги и ученики разъяснили мне, что нуль входит также и в множество неположительных чисел, а заодно и в множество неотрицательных чисел. Но Серр, кроме указанных неравенств, доказал еще одно свойство нуля: он оказывается вдобавок числом натуральным.
Вот это (поразительное, на мой взгляд) доказательство:
"Некоторые (намек на Арнольда. - В. А.) считают, что натуральные числа - это те, которые участвуют в натуральном (то есть естественном) счете: "один, два, три...". Но такой экспериментаторский подход ненаучен. С точки зрения нашей высокой науки, "естественный счет" никакого отношения к теории не имеет. Научное определение таково: "Натуральные числа - это мощности конечных множеств". А какое из конечных множеств - самое главное? Разумеется, пустое! Значит, его мощность, то есть нуль, - натуральное число!".
В уже упомянутом руководстве для первокурсников все это используется для определения факториала. Вот это определение: во-первых, 0! = 1; во-вторых, для любого натурального числа n имеет место равенство (n + 1)! = (n + 1)n!.
Если не знать, что нуль - натуральное число, то ни одного факториала невозможно ни определить, ни понять, ни вычислить. Кстати, обычное определение n! = 1* 2 * ... * n, во-первых, не фигурирует в этом тексте нигде, и, во-вторых, считается ошибочным. А именно: во-первых, участвующие в этом определении три точки не определены, а во-вторых, определение не годится ни для n = 0, ни для n = 1.
Раз уж я стал разбирать это руководство, процитирую из него еще одно место. Речь идет теперь об определении науки математики, чтобы студенты знали, что им предстоит:
"Математика есть наука о доказательствах, доказательства это цепочки импликаций: (из А вытекает В, из В вытекает С) - цепочка; вывод: доказано, что из А вытекает С. Итак, самое главное - понять, что такое одна импликация. Вот ее определение. Пусть А и В - два произвольных высказывания. Если оба они верны, то говорят, что из А вытекает В".
На мой непросвещенный взгляд, такая точка зрения на импликации (а следовательно, и на доказательства, и на математику) - чистое мракобесие. При таком определении из того, что дважды два четыре, следует, что Земля вращается вокруг Солнца. Студента, понимающего выводы и доказательства подобным образом, уже бесполезно учить какой-либо естественной науке: мракобесие уничтожает естествознание как таковое. По этой мракобесной логике Галилея поделом наказывали: он ведь говорил о своих доказательствах вращения Земли и других подобных фактов совсем в другом смысле.
Авторы инструкции для младшекурсников, видимо, чувствовали, что они что-то не договорили, а потому добавили к своему определению импликации примечание.
"Пусть опять даны два утверждения A и В, но на этот раз утверждение А ложно. Тогда тоже говорят, что имеет место импликация "из А вытекает В", даже независимо от того, верно В или нет".
Впрочем, авторы обещают в дальнейшем этим примечанием не пользоваться.
Из других бурбакистских принципов, упомянутых Серром, назову еще утверждение о полной независимости математики от физики. В одном своем письме ко мне Серр уже заявил, что "у математики и физики нет ничего общего", но он добавил тогда, что "не станет публиковать этого утверждения, потому что нам, математикам, не следует высказываться по философским вопросам, ибо самые лучшие из нас способны высказать здесь совершеннейшую чушь".
Я считаю это письмо бумерангом (бумеранг - оружие, убивающее самого охотника подобно другому письму Серра, где он отказался участвовать в подготовке книги Международного математического союза (Mathematics: Frontiers and Perspectives, IMU-AMS, 2000 подводящей математический итог столетию, мотивируя это тем, что, по его опыту, "в математике все коллегиальные предприятия - сплошные неудачи". У Бурбаки не бывает официального лидера, но Серр, я думаю, фактически был лидером этого коллегиального предприятия пару десятков лет.
Первый же бумеранг Серра неожиданным образом повлиял на школьную реформу в России. Осенью 2000 г. в Москве проводилось большое заседание по вопросу "нужно ли преподавать математику в гуманитарных вузах (экономистам, историкам, юристам, филологам, психологам и т.д. и если нужно, то какую?". Несколько часов я слушал на этом заседании выступления тех, кто ее уже преподает. В основном я понял такую идею: для гуманитарных наук важнее всего сейчас компьютеризация, поэтому нужна та математика, какую использует компьютер. Следовательно, самым главным должен быть солидный (уж не помню, годовой или двухгодовой) курс теории пустых множеств, видимо, для понимания булевой алгебры, в которой работает компьютер.
Затем слово взял один настоящий математик, который заявил:
"Я хочу выступить здесь против Арнольда" (последний к этому моменту ничего еще не говорил. - В.А.). А именно, Арнольд в одной своей статье писал, что Гильберт в 1930 г. в статье "Математика и естествознание" утверждал, что геометрия - часть физики, в то время как один крупнейший французский математик сейчас утверждает, что математика и физика не имеют ничего общего. Арнольд делает вывод, что эти два утверждения противоречат друг другу. Но противоречие получается только у тех, кто в силу своей недостаточной интеллектуальной подготовки не читал Аристотеля (или не понял его). Я же Аристотеля понял, и поэтому просто прихожу из этих двух утверждений к выводу: геометрия не имеет с математикой ничего общего и потому должна быть исключена из всех математических курсов - от средней школы до университетов".
Через пару месяцев я получил от министра просвещения проект нового школьного образования с указанием числа часов на каждый предмет в каждом классе. И геометрия была исключена вовсе (видимо, под влиянием выступавшего математика, который, вдобавок, был ранее по моей инициативе избран Отделением математики РАН своим представителем в министерстве). Ученый совет Математического института им. В.А. Стеклова РАН в ответ на исключение геометрии из министерского плана написал министру письмо, указывая на необходимость геометрии для полноценного среднего образования, причем не только как части математики, но и как части общей культуры, как тренировки мышления, а также ради использования в физике, технике и т.д. Через несколько недель геометрию вернули на место. Позже коллеги из Дубны говорили мне, что, кроме Математического института, протестовали также представители оборонных предприятий: "без геометрии не будет ни бомб, ни ракет".
Антифизические идеи в математике давно популяризируются самыми разными ее представителями. Г. Харди, например, объяснял (в недавно изданной по-русски "Апологии математика") слова Гаусса "теория чисел - королева математики" сходством теории чисел с королевой: это сходство заключается, согласно Харди, в полной бесполезности обеих. Недавно эта бурбакистская идея получила новую формулировку, принадлежащую одному из крупнейших математиков Германии, содиректору Математического института им. М. Планка в Бонне Ю.И. Манину (опубликована в той же книжке о перспективах математики, в которой отказался участвовать Серр).
Теория Манина состоит из трех частей.
Во-первых, он определяет математику как раздел филологии или лингвистики: это наука о формальных преобразованиях одних наборов символов некоторого конечного алфавита в другие при помощи конечного числа специальных "грамматических правил". Отличие математики от живых языков состоит, по Манину, лишь в том, что в ней больше грамматических правил. Например, имеется правило, позволяющее заменять символы "1+2" на "3".
Второй тезис Манина основан на том, что любому человеку с непредвзятым мышлением ясно: подобным переливанием из пустого в порожнее нельзя открыть ничего нового. Если все же в конце и получается что-то интересное, то это означает просто, что оно содержалось уже в исходных данных. Поэтому общество, правительства и т. п. не хотят оплачивать все это бессмысленное переливание из пустого в порожнее. Но математики хотят получать стипендии, гранты и тому подобное. Для этой цели они изобрели университеты и факультеты, где студентов обучают претендовать на открытия (которые им недоступны в силу самого характера их деятельности, как объяснено выше). В этом, по Манину, состоит сущность математического образования: это просто обучение претенциозности.
Третий тезис был добавлен к двум первым после того, как я (во время Международного математического конгресса 1998 г. в Берлине) оспорил первые два. "Некоторые, - пишет Манин, не называя меня, - возражают, утверждая, будто математика полезна в физике, технике и вообще для прогресса человеческой цивилизации. Но они заблуждаются. Чем математика действительно полезна, так это своим огромным вкладом в решение основной проблемы современного постиндустриального человечества. Проблема же эта состоит вовсе не в том, чтобы, как думают некоторые, ускорять прогресс человечества, а напротив, в том, чтобы этот прогресс всемерно тормозить. Математика отвлекает умных людей от действительно опасных для человечества занятий. Если бы вместо проблемы Ферма умники усовершенствовали бы автомобили или самолеты, вреда человечеству было бы больше".
Многие спрашивают меня, не шутка ли все это. Но речь идет о серьезной теории, завершающейся следующим рассуждением. Проблема Ферма более не способна отвлекать: она решена Э. Уайлсом. Поэтому следует указать новые столь же бесполезные и малоинтересные вопросы, чтобы отвлечь следующие поколения математиков. Исходя из этого, Манин посвящает заключительные 90% своей статьи перечню подобных задач.
Вернусь к своему дуэльному докладу.
Я его начал с упоминания старого русского (а возможно, даже византийского?) обычая: "о покойниках плохо не говорят", и хотя вся дискуссия была озаглавлена "Вокруг Бурбаки", я продолжил: "поэтому о Бурбаки я говорить не буду" (о его смерти официально было объявлено несколько лет назад). Мой доклад назывался "Математика и физика", и его я здесь пересказывать не стану, так как моя статья "Математика и физика: родитель и дитя или сестры?" опубликована в "Успехах физических наук" (1999, N 12). Ради юбилея Академии наук редакция поместила в этом выпуске несколько необычных для физического журнала статей, в том числе статьи К. Вейерштрасса и К. Якоби.
Одну фразу из этой своей статьи я все же упомяну, потому что физики настолько обиделись на меня за нее, что не включили ее в русское издание (в английской версии она есть). Статья начинается с пары эпиграфов, описывающих обе науки. Первый принадлежит Стендалю: "Я любил и теперь еще люблю математику ради нее самой, как не допускающую лицемерия и неясности, которые мне отвратительны". Второй (выкинутый редакцией) эпиграф подчеркивает кардинальное отличие точки зрения физиков на лицемерие: "t us put a = 0, though it does not make any sense and is not quite correct from the viewpoit of quantum mechanics" (E. Schroedinger. "Statistical thermodynamics") *.
* "Давайте примем a = 0, хотя это не имеет какого-либо смысла и не является корректным с точки зрения квантовой механики" (Э. Шредингер. Статистическая термодинамика"). - Ред.
В своем дуэльном докладе я упомянул о большом влиянии на Бурбаки идеологии Декарта, четыре принципа которого состояли в следующем.
Не следует экспериментально проверять исходные положения наших теорий: это просто произвольные аксиомы, и их отношение к реальности отношения к науке не имеет.
Столь же бессмысленно сравнивать с реальностью и окончательные выводы: вряд ли они согласуются с ней лучше исходных аксиом.
Что действительно важно - это по строгим правилам логики преобразовывать аксиомы в конечные результаты, избегая всякого участия воображения. Чтобы сделать геометрию наукой, необходимо изгнать из нее чертежи - это следы экспериментов, с одной стороны, и пища для воображения - с другой. Вместо кривых и поверхностей нужно рассматривать идеалы и модули, делая геометрию чисто аналитической.
Нужно немедленно запретить все другие методы преподавания, кроме моего (Декарта. - В. А. ибо он один является политически корректным: при этом методе самые посредственные умы продвигаются столь же быстро, как и самые блестящие.
Интересно, что "Оптика" Декарта - его основная книга, где он, в соответствии со своими принципами, обнаружил, что скорость света в воде на 30% больше, чем в воздухе (вопреки теориям Ферма, Гюйгенса и других, из которых получается противоположный вывод: скорость света в воде на 30% меньше) - впервые была опубликована в 1996 г. Думаю, что Декарт, хотя и опровергал мнения своих предшественников и современников, все же опасался их возражений. (Отмечу, что уже упомянутая статья К. Якоби в "Успехах физических наук" называется "О жизни Декарта и его методе направлять ум правильно и изыскивать в науках истину".)
Упомяну еще некоторые удивительные сведения из истории математики и физики, которые я сообщил совершенно незнакомой с ними французской аудитории. Начну с того, что восхищение ролью Евклида и Пифагора в развитии геометрии основано на своеобразных преувеличениях. Историкам уже больше сотни лет известны факты, о которых я расскажу, но математики никогда о них не знали.
Много тысячелетий назад (заведомо до Моисея) в Египте жил замечательный математик, сделавший массу открытий. Он был землемером (отсюда "геометрия") фараона, и известно лишь имя, которое он получил при посмертном обожествлении, - Тот (в функции этого бога на том свете входила перевозка душ умерших в лодке через Стикс или Лету древнего Египта). Первое его математическое открытие - натуральный ряд: он обнаружил, что самого большого целого числа нет (идея актуальной бесконечности до него числа исчерпывались суммой налога фараону. Тот научился проводить доказательства, основанные на факте существования актуальной бесконечности.
Вторым я назову не вполне математическое открытие: изобретение первого фонетического алфавита. До этого письменность в Египте была только иероглифической. Тот же уменьшил число символов до нескольких десятков, сообразив, что, скажем, звук "с" можно всегда изображать упрощенным иероглифом, ранее означавшим слово "собака".
В диалоге Платона "Федр" описано обсуждение Тотом и главным египетским богом Аммоном изобретения алфавита. Тот утверждает, что способность записывать информацию сделает людей гораздо умнее, так как им не придется все запоминать, а можно будет тратить ум на размышления. Аммон же возражает, говоря, что, хотя люди восхищены изобретением, умнее они не станут. "Напротив, - говорит он, - они станут глупее, так как отвыкнут думать, полагаясь на свои записи". (Компьютеризацию тогда еще не обсуждали.) Финикийский и еврейский алфавиты произошли от египетского алфавита Тота, а от финикийского - греческий, а от него впоследствии - и римская латиница, и наша кириллица.
Третье изобретение Тота - геометрия. Он придумал (ради измерения площадей участков, чтобы знать и ожидаемый урожай, и налог, и нужное для полива количество нильской воды) и аксиомы, и теоремы, и определения, и построения. Единственное, в чем он не дошел до современного уровня, было то, что он совершенно не интересовался независимостью своих аксиом. Например, вместо аксиомы параллельных Евклида, он ввел, кажется, четыре или пять разных аксиом, каждая из которых на самом деле влечет за собой все остальные. Но он этого не доказывал, а просто пользовался всеми "аксиомами", и честь выбрать из этих аксиом одну ("пятый постулат" а остальные превратить в теоремы принадлежит Евклиду.
Среди геометрических достижений того времени (если не самого Тота, то его учеников) - замечательное измерение радиуса земного шара. От Фив до Мемфиса караваны верблюдов шли почти по меридиану, и посчитать число шагов (то есть расстояние) не составляло труда. Измерить разность высот Солнца в полдень в один и тот же день в обеих столицах Египта тоже сумели. После этого радиус легко вычислить; удивительно, однако, что относительная ошибка этого измерения составляла всего 1% (по сравнению с современными измерениями).
Греки провели измерение Земли заново (через пару сотен лет). Не располагая Нилом, они решили использовать Средиземное море и проплыли на север от устья Нила до острова Родос. Расстояние они измерили, умножив "скорость корабля при ветре средней силы" на время путешествия. Размер Земли при этом получился вдвое больше правильного (считать верблюжьи шаги легче, чем оценивать, средней ли силы ветер).
Интересно, что много столетий спустя один генуэзский капитан пришел к католической королеве с просьбой отправить его в Индию западным путем (вместо восточного, впоследствии пройденного Васко де Гамой). Королева тотчас назначила экспертную комиссию и вскоре отказала капитану, потому что, дескать, "невозможно построить корабль, который вместил бы столько бочек пресной воды, сколько нужно, дабы доплыть так далеко". Но капитан спорил, и после нескольких туров дискуссий с экспертами ему позволили рискнуть умереть от жажды (говорят, вся дискуссия основывалась на том, что эксперты верили греческой оценке размеров Земли, а капитан - египетской). Вот как была (случайно) открыта Америка.
Тот основал в Египте звездочетство и небесную механику. Если и не он сам, то, во всяком случае, его древние последователи знали закон обратных квадратов (притяжения планет Солнцем законы Кеплера и вывод одного из другого. Ньютон писал, что, поскольку этот вывод сгорел (вместе с семью миллионами других научных книг) в пожаре Александрийской библиотеки, где хранилась вся наука древнего Египта, то ему (Ньютону) "принадлежит честь восстановления этого древнего доказательства". В греческой и средневековой версии Тот именовался "Гермесом Трисмегистом" ("трижды величайшим") и его труды переиздавались чуть ли не ежегодно под названием "Изумрудная скрижаль" - у Ньютона дома было несколько ее изданий.
В VII в. до н.э. римский царь Нума Помпилий (следующий после Ромула) построил на форуме храм Весты, внутри которого был гелиоцентрический планетарий. В центре горел факел, изображавший Солнце. Вокруг него каждую планету (Меркурий, Венеру, Землю с Луной, Марс, Юпитер, Сатурн - а больше они не знали) носила по кеплеровой эллиптической орбите назначенная для этого весталка (учитывая и период обращения, и закон площадей). Если кто хотел найти на небе, скажем, Сатурн, то он шел в храм Весты, становился около "Земли", смотрел, где сейчас держат "Сатурн", замечал направление и потом, выйдя из храма, обнаруживал настоящий Сатурн, глядя по этому направлению.
В средние века научные книги истребляли, кроме лишь "практически полезных" - по артиллерии, мореплаванию и архитектуре. В книге Витрувия по архитектуре (1 в. н.э.) я видел среди полезных для архитектора кривых описание эллипса, сопровождающееся рассказом о его астрономических приложениях в теории движения планет. И Ньютон, и Коперник знали об этих древних гелиоцентрических теориях и цитировали их, но эта древность мало кого интересовала.
Среди других многочисленных изобретений Тота - игра в шашки, придуманная им как демократизация слишком сложных шахмат. Последние существовали вдобавок в двух вариантах; во втором фигуры означали целые армии, и на каждой была надпись, указывающая численность армии, а битва иногда не уничтожала фигуру, то есть армию, а только уменьшала ее численность.
Пифагор был одним из первых в мире, как это сейчас называется, индустриальных шпионов. Он провел в Египте около двадцати лет. Египетские жрецы обучили его своим наукам, но потребовали от него подписку о неразглашении (вследствие чего он никогда ничего и не публиковал). Теорема Пифагора была опубликована (в Вавилоне клинописью) за пару тысяч лет до него, вместе с доказательством и с формулой для нахождения Пифагоровых троек (вроде 32 + 42 = 52 описывающих все прямоугольные треугольники с целыми длинами сторон. Кроме геометрии (о которой он рассказал своим греческим ученикам, донесшим ее до Евклида, уже не связанного подпиской о неразглашении и опубликовавшего эту тотовскую геометрию Пифагор вывез из Египта независимую от индусской теорию переселения душ, базирующееся на ней вегетарианство и еще основы теории гармонии струнных музыкальных инструментов (формулу натяжения струн разных длин для получения одинаковой частоты - натяжение пропорционально квадрату длины; условия получения октавы, терции, квинты... - в сущности, теорию рядов Фурье).
Другими подобными Пифагору переносчиками египетских тайн в Грецию и в Европу были Платон (логика, философия) и Эвдокс (теория чисел, включая алгоритм Евклида и теорию иррациональных чисел типа теорий сечений Дедекинда или колец Тротендика). Последняя теория началась с открытия несоизмеримости диагонали квадрата с его стороной (то есть с иррациональности числа Ц2 которое в пифагорейской школе было засекречено. Дело в том, что этот факт подрывал значение арифметической теории дробей (и тем самым всей математики): дроби оказывались недостаточными для потребностей физики (для измерения всевозможных длин а следовательно, математики занимаются ненужной чепухой, их следует прогнать или по меньшей мере не кормить.
Пришлось добавлять к арифметике дробей новую науку - теорию вещественных чисел. Эту не такую уж простую задачу Евдокс блестяще решил, и сейчас удивительно, насколько его подход близок к современным (как в этом вопросе, так и в теории делимости и диофантовых уравнений). Открытие того, что такие факты, как однозначность разложения целого числа на простые множители, нуждаются в доказательствах, на самом деле не менее важно, чем проведение самого (впрочем, неочевидного) доказательства.
Из всего рассказанного мне казалось очевидным, что математика - это часть физики, а вовсе не наука о переливании из пустого в порожнее (как утверждает Манин и как думал Гильберт до теоремы Геделя, установившего невыполнимость программы Гильберта полной формализации математики). И математика, и физика - экспериментальные науки, разница лишь в том, что в физике эксперименты стоят миллиарды долларов, а в математике - единицы рублей.
Что же касается результата дуэли, то из нескольких сот слушателей со мной были согласны, по моей оценке, примерно 3/4. Но зато присутствовавшие математики все, как один, были на стороне Серра (или, во всяком случае, на это претендовали, ведь говорить иное было бы для них опасно). Известно, что французский министр просвещения (геофизик желая понять, как учат математике детей, спросил одного отличника-младшеклассника: "Сколько будет два плюс три?" Бурбакисты-учителя не научили мальчика считать, и он не знал, что это 5, но он ответил так, как они с него требовали в школе: "Это будет 3 + 2, так как сложение коммутативно". Министр объявил, что такое обучение никуда не годится, что подобных учителей "математиков" надо гнать из школ, а считать детей пусть учит кто угодно другой - химик, инженер и т.п. Но результат подтвердил социальную устойчивость бурбакизма: министра сняли с поста (и даже его министерство не сохранили, а разделили на два независимых).
Четвертый принцип Декарта очень привлекателен для начальства. Лев Толстой уже отмечал, что всякое правительство естественным образом склонно бороться против образования своего народа: оно боится, что народ начнет понимать его поступки, поэтому стремится оставить его невежественным (письмо к А.М. Калмыковой; см. Толстой Л.Н. Соч. Т. 19. М., 1984. С. 364). Вот почему бурбакистская мафия, заменяющая понимание науки формальными манипуляциями с непонятными "коммутативными" объектами, так сильна во Франции, и вот что угрожает и нам в России.
прочитаю попозже. Могу не читая сказать - с огромной вероятностью там внутри будет, что французские школьники считают, что 5+3 это 3+5
Достаточно прочитать только тот абзац, который я выделил жирным, после чего умиротворённо улыбнуться.
Ибо точка зрения Арнольда и так общеизвестна. Кстати, имхо в мней очень много мудрости.
Ибо точка зрения Арнольда и так общеизвестна. Кстати, имхо в мней очень много мудрости.
Арнольд, как всегда, тонок, ироничен, неотразим и обаятелен!  В общем, понравилось.
В общем, понравилось.
 В общем, понравилось.
В общем, понравилось.я с ним лично общался, в максимально вежливой манере. отвечал максимально грубо. я не обижен, просто как факт. спрашивал я его точно не тупые вещи.
Это он может, да. Сам присутствовал при том, как он кому-то отвечал как бы это сказать поточнее... в весьма эксцентричной и экстравагантной манере.
Со мной говорил вежливо, но мы правда и беседовали о чём-то нейтральном, не помню уже о чём.
Со мной говорил вежливо, но мы правда и беседовали о чём-то нейтральном, не помню уже о чём.
М-да, неприятный штрих к портрету знаменитости  Впрочем, за гениями такое водится.
Впрочем, за гениями такое водится.
 Впрочем, за гениями такое водится.
Впрочем, за гениями такое водится.А, кстати, на мехмате он сейчас чего-нибудь читает или ведет?
по-моему на форуме писали, что он на публичной лекции в ГЗ выгнал какого-то мужчину, который, как ему показалось, громко что-то шепнул кому-то.
Знаешь, вообще, эти академики - они люди странные. К их мнению стоит прислушиваться, но жить своим умом всё же. То есть если не будешь гнуть свою линию, то и грош тебе цена, ведь академику-то, в сущности, ты никто, а сам себе ты очень важный человек.
Расскажу историю. Когда я был третьекуром Нижегородского Госуниверситета, я решил перевестись на мехмат МГУ. Но сомневался. Тогда я приехал в Москву, жил у друзей родителей и неделю изучал мехмат: приходил на факультет к 9:00 (когда первая пара начинается) и уходил в 20:30 (когда последний спецсем заканчивается). Ходил на все виды занятий всех курсов, составлял впечатление. И всех спрашивал - так мол и так, думаю не перевестись ли мне, что посоветуете. И люди много разного мне говорили, а я слушал.
В частности, отловил я после лекции Фоменко и произошёл между нами такой диалог, цитаты не точные, передаю только идею, но не конкретные фразы. Это была моя первая в жизни встреча с живым легендарным Фоменко.
Я: Так мол и так, я студент мехмата ННГУ, вот думаю не перевестись ли мне, что посоветуете - стоит переводиться?
Фоменко: Конечно, нет! У нас тут и своих разгильдяев хватает!
Я: Но я вроде как хотел заниматься наукой, идти в аспирантуру...
Фоменко: Да? Ну тогда переводитесь! А то никто не хочет заниматься наукой!
Вот такие вот дела. Так что относитесь к словам крупных людей с осторожностью: их слова могут быть и верны, но не учитывать специфики ситуации и быть поэтому сродни удару из пушки по воробьям. И если тот же Арнольд кому-то когда-то нагрубил, не делайте из этого глобальных поспешных выводов: не умно это - спешить с выводами.
Самому, в общем, голову надо на плечах иметь, вот я что скажу
Мои советы достаточно категоричны, но всё это на самом деле моё имхо и по большому счёту я никого ни к чему не склоняю.
Расскажу историю. Когда я был третьекуром Нижегородского Госуниверситета, я решил перевестись на мехмат МГУ. Но сомневался. Тогда я приехал в Москву, жил у друзей родителей и неделю изучал мехмат: приходил на факультет к 9:00 (когда первая пара начинается) и уходил в 20:30 (когда последний спецсем заканчивается). Ходил на все виды занятий всех курсов, составлял впечатление. И всех спрашивал - так мол и так, думаю не перевестись ли мне, что посоветуете. И люди много разного мне говорили, а я слушал.
В частности, отловил я после лекции Фоменко и произошёл между нами такой диалог, цитаты не точные, передаю только идею, но не конкретные фразы. Это была моя первая в жизни встреча с живым легендарным Фоменко.
Я: Так мол и так, я студент мехмата ННГУ, вот думаю не перевестись ли мне, что посоветуете - стоит переводиться?
Фоменко: Конечно, нет! У нас тут и своих разгильдяев хватает!
Я: Но я вроде как хотел заниматься наукой, идти в аспирантуру...
Фоменко: Да? Ну тогда переводитесь! А то никто не хочет заниматься наукой!
Вот такие вот дела. Так что относитесь к словам крупных людей с осторожностью: их слова могут быть и верны, но не учитывать специфики ситуации и быть поэтому сродни удару из пушки по воробьям. И если тот же Арнольд кому-то когда-то нагрубил, не делайте из этого глобальных поспешных выводов: не умно это - спешить с выводами.
Самому, в общем, голову надо на плечах иметь, вот я что скажу

Мои советы достаточно категоричны, но всё это на самом деле моё имхо и по большому счёту я никого ни к чему не склоняю.
Мои советы достаточно категоричныне в обиду будет сказано, советы весьма тривиальны. Ну кто интересно совет " прислушивайся к мнению великих, но и свою голову на плечах имей" посчитает категоричным.
Поясните в двух словах метод ортогонализации Шварца.
Заранее спасибо.
Заранее спасибо.
давайте без флуда
Поясните в двух словах метод ортогонализации Шварца.Это то же самое, что ортогонализация системы векторов по Граму-Шмидту или нет?
Заранее спасибо.
да, это оно. я правда не знаю, как кратко обьяснить
Я знаю как, но устал сейчас сильно, не буду писать. Если действительно надо, погулите, тема боян, изложена в любом учебнике по линалу наверняка.
Там основной факт в том, что грамиан (определитель матрицы Грама) всегда неотрицателен, и равен нулю тогда и только тогда, когда векторы линейно зависимы. Матрица Грама - это матрица, элементами которой являются попарные скалярные произведения векторов набора. Матрица Грама ортонормированной системы векторов единичная.
Если больше нигде не найдёте - пишите приват, наберу и вышлю хороший понятный матричный алгоритм ортогонализации, если правда очень надо.
Там основной факт в том, что грамиан (определитель матрицы Грама) всегда неотрицателен, и равен нулю тогда и только тогда, когда векторы линейно зависимы. Матрица Грама - это матрица, элементами которой являются попарные скалярные произведения векторов набора. Матрица Грама ортонормированной системы векторов единичная.
Если больше нигде не найдёте - пишите приват, наберу и вышлю хороший понятный матричный алгоритм ортогонализации, если правда очень надо.
Спасибо и на то, что сказали, что метод Шварца есть Греммы Шмита......
просто метода ортогонализации Шварца нигде не нашлось......
ещё раз спасибо !
просто метода ортогонализации Шварца нигде не нашлось......
ещё раз спасибо !
короче обьясняю. предположим есть линейное пр-во и вектор, не лежащий в нем. если из этого вектора вычесть его проекцию на пространство, то получится очевидно ортогональный вектор. Теперь стартуем с первого вектора базиса и постепенно добавляем остальные. собственно все...
Да, всё так.
Если из каких-то других соображений известно, что векторы линейно-независимы, то процесс ортогонализации можно применять и к бесконечным системам векторов. Если система векторов конечная, то критерием линейной независимости является невырожденность матрицы Грама. Если система более, чем счётная, то в общем случае придётся применять трансфинитную индукцию.
Если из каких-то других соображений известно, что векторы линейно-независимы, то процесс ортогонализации можно применять и к бесконечным системам векторов. Если система векторов конечная, то критерием линейной независимости является невырожденность матрицы Грама. Если система более, чем счётная, то в общем случае придётся применять трансфинитную индукцию.
Если система более, чем счётнаяхоспади, ну кому нужны несепарабельные гильбертовы пространства?
хоспади, ну кому нужны несепарабельные гильбертовы пространства?Это уже не моё дело. Я на вопрос отвечал.
Каково твоё отношение к этому конфликту?слышал, но стараюсь не обращать внимание.
ясно
нормальная здоровая позиция для молодого человека да и вообще для того, кому наука интереснее околонаучных сплетен
нормальная здоровая позиция для молодого человека да и вообще для того, кому наука интереснее околонаучных сплетен
ликвидация безграмотности.. угадайте кто.
Подсказка - нереально крут.

Подсказка - нереально крут.

Гипотеза: Брайан Грин?
упс.. зачот


ликвидация безграмотности.. угадайте кто.Продолжаем серию портретов-загадок.
Подсказка - нереально крут.

Чебышев ?
реально, ровно такая же мысль возникла
Чебышев ?Верно.
Пафнутий Львович Чебышёв.
Теперь ты загадывай!
это будет тяжелая загадка, в оправдание скажу что нереально крут, 
да и это, Чебышев мало отношения к диффгеометрии имеет


да и это, Чебышев мало отношения к диффгеометрии имеет


это будет тяжелая загадка, в оправдание скажу что нереально крут,м.б. Яу?
да и это, Чебышев мало отношения к диффгеометрии имеетНу и что? Ты свою песню поёшь, я - свою

>>м.б. Яу?
фотка Яу в начале треда
>>Ну и что? Ты свою песню поёшь, я - свою
ну топик то диффгеометрии посвящен, а не математике вообще.. еще запости какого-нить дискретного или вычислительного математика, или из какой-нить подобной хуйни, утрирую конечно
фотка Яу в начале треда
>>Ну и что? Ты свою песню поёшь, я - свою
ну топик то диффгеометрии посвящен, а не математике вообще.. еще запости какого-нить дискретного или вычислительного математика, или из какой-нить подобной хуйни, утрирую конечно
terence tao 

нет.. фотка Terence Tao будет через месяц, топикстартер будет иметь честь общаться и сделает эксклюзивное фото.. 



да я уже сам понял...он моложе выглядит...
какого-нить дискретного или вычислительного математика, или из какой-нить подобной хуйниЭ-э-э, поаккуратнее.

где он не прав)?
Не знаю, кто этот азиат на фото. Подскажи?
Давай пока сам загадаю. Сложность в том, что фотка в молодости. Скорее всего, ты знаешь этого чувака. Он классный. И отличный лектор.

Давай пока сам загадаю. Сложность в том, что фотка в молодости. Скорее всего, ты знаешь этого чувака. Он классный. И отличный лектор.

где он не прав)?Не гнобите да не гнобимы будете!

Скорее всего, ты знаешь этого чувакакстати он меня тоже знает

кстати он меня тоже знаетСкинь что ли в приват имя, чтоб и я знал, что ты его знаешь

Похоже, у нас с тобой общий знакомый. То, что он меня знает - факт, мы с ним на дискотеке пиво пили и на тачке катались. Помнит ли он это - я хз. Давно было, в зимой 2004/2005, кажется.
ладно, это сложная была, Кенджи Фукайя.. потом полегче загадаю, у Гонобобеля Марсело Виана
Кенджи Фукайя
Кто это?
у Гонобобеля Марсело ВианаВерно.
крутой дифф. и алгебр. геометр
Спасибо.
А результаты основные какие?
А результаты основные какие?
Категория Фукайи предположительно является ключем к пониманию 'зеркальной симметрии', которая в свою очередь математическая 'тень' суперсимметрии.
А суперсимметрия это как грится одна из основ совр. физеки.
А суперсимметрия это как грится одна из основ совр. физеки.
Категория ФукайиВас ис дас?
ну это некий обьект на пересечении чисто алгебр. геометрии и многообр. Калаби-Яу
Идея ясна, подробности вряд ли осилю.
Спасибо.
Спасибо.
Можешь сказать что-нибудь про петлевую гравитацию? Чем она с математической точки зрения отличается от струн, какие у этой теории перспективы?
чисто имхо, никаких
честно говоря не специалист. у меня на предзащите был один из оппонентов - специалист по петлевой гравитации. насколько я понимаю из краткого разговора с ним - это не мейнстрим.. Хотя сейчас не совсем понятно что мейнстрим, много людей разочаровываются в струнах, и циркулируют слухи что даже сам Виттен огорчен отсутствием предсказательной силы
ясно, спасибо
Кстати, вопрос на засыпку ( несложный) - почему с точки зрения физика группа движений нашего пространства не SO(3 а SU(2).
Кто заранее знал - молчите.
Кто заранее знал - молчите.
Не совсем понял вопрос. Можно обе использовать, они локально изоморфны. Просто в SU(2) содержится еще информация о фазе, вот ее для квантового случая и используют.
ну я имел ввиду, что физическое движение, в отличие от математического, определяется не просто начальным и конечным положением,а еще и путем, по которому пришли к положению ( поскольку мы же не телепортируемся, а движемся)

491593
спрашивайте, постараюсь помочь.