Как найти уравнение кривой по картинке?
на глаз похоже на параболу
что там с софтом - не знаю
в детстве помнится на бейсике были программы для полиномиальной регрессии
что там с софтом - не знаю
в детстве помнится на бейсике были программы для полиномиальной регрессии
Похоже на параболу )
Не знаю, как в Математиках и Статистиках, но если очень надо, то такое можно проделать ручками.
Ключевые слова: интерполяция многочленами, интерполяция сплайнами, многочлены Лагранжа, многочлены Ньютона
Не знаю, как в Математиках и Статистиках, но если очень надо, то такое можно проделать ручками.
Ключевые слова: интерполяция многочленами, интерполяция сплайнами, многочлены Лагранжа, многочлены Ньютона
V origine tochno est. pro drugie neznau.
такое можно проделать ручками.Я бы рада, но не знакома с этой кухней... Поэтому и хочу с помощью уже готовых программ это сделась. А, если не лень, ну посчитайте мне ручками )
Ключевые слова: интерполяция многочленами, интерполяция сплайнами, многочлены Лагранжа, многочлены Ньютона
выложи оцифрованную таблицу x-y, попробую
выложи оцифрованную таблицу x-y, попробую12.0000 105.1087
12.2867 98.0435
12.8602 81.1957
13.5054 76.8478
13.9355 65.1630
14.0072 69.2391
14.4373 62.9891
15.0108 58.9130
15.9427 53.2065
16.9462 46.1413
17.9498 39.0761
18.9534 36.3587
19.8853 35.8152
19.9570 33.0978
20.8889 31.1957
21.8208 29.5652
22.8244 30.3804
22.8961 26.8478
23.8996 24.9457
24.9032 23.5870
25.9068 21.9565
25.9785 23.5870
26.9821 20.8696
27.9857 20.8696
28.9176 21.1413
29.9928 19.7826
30.9964 21.4130
32.0000 21.1413
Это для экспериментальных точек, а не для уже построенного графика на картинке.
V origine tochno est. pro drugie neznau.установила себе ориджин. Ну, и как это делается там? Буду искать мануалы пока никто не отвелил...
Для фиттинга параболой получается так:
y = 250,04363 -17,11321*x + 0,31685*x^2
Для четвертой степени получается так:
y = 980.77483 - 154.61497*x + 9.57159*x^2 -0.26563*x^3 + 0.00276*x^4
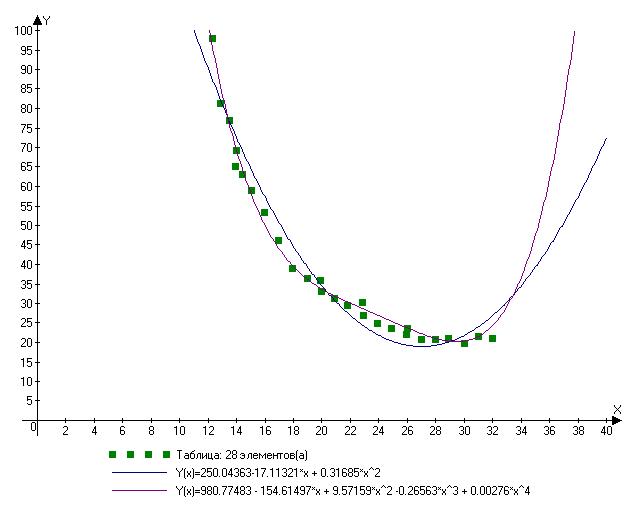
Пока не очень сорошо получается. Имхо, нужно подбирать кривую по параметрам y = C1(x-29)^a + 20
y = 250,04363 -17,11321*x + 0,31685*x^2
Для четвертой степени получается так:
y = 980.77483 - 154.61497*x + 9.57159*x^2 -0.26563*x^3 + 0.00276*x^4
Пока не очень сорошо получается. Имхо, нужно подбирать кривую по параметрам y = C1(x-29)^a + 20
Пока не очень сорошо получаетсяСпасибо! 4-той степенью лучше подходит, да? Уж очень точно не нужно, т.к. это лишь экспериментальные данные и всё сильно от зародышей зависит )
Спасибо! 4-той степенью лучше подходит, да? Уж очень точно не нужно, т.к. это лишь экспериментальные данные и всё сильно от зародышей зависит )
А по какому принципу вибирается уравнение для фитирования? Как выбрать, на угад?
А по какому принципу вибирается уравнение для фитирования? Как выбрать, на угад?
Естесственно, чем больше параметров, тем лучше сойдется с экспериментальными точками. Но, например, 4я степень плохо себя ведет после 30 градусов. Если тебе нужно пользоваться этой формулой после 30 градусов, то лучше не стоит ее использовать.
Уравнение построено с помощью Origin. У меня Origin 7.5, строил так: перетащил тхт с точками в ориджин, он его съел, пофвилась таблица x- y в ориджин. Затем нанес это на график (plot - Scaterвыбрал иксы и игреки, пофвился график. Потом Tools -> Polynomial Fit, появилось меню с выбором параметров подгонки. Выбрать нужную степень, нажать fit, появится на графике. Сами параметры будут написаны в окошке логов справа внизу.
Уравнение построено с помощью Origin. У меня Origin 7.5, строил так: перетащил тхт с точками в ориджин, он его съел, пофвилась таблица x- y в ориджин. Затем нанес это на график (plot - Scaterвыбрал иксы и игреки, пофвился график. Потом Tools -> Polynomial Fit, появилось меню с выбором параметров подгонки. Выбрать нужную степень, нажать fit, появится на графике. Сами параметры будут написаны в окошке логов справа внизу.
А вообще исходя из биологического смысла, тут должна быть гипербола...которая существует от 12 до 32 градусов.
нет, после 30 особо не нужно, зародышам уже плохо при такой температуре
Вообще, лучше оцифровать не экспериментальные точки, а точки с кривой теоретической. Тогда результат будет лучше, я думаю.
Вот для кривой:
11.7842 105.1087
12.1439 97.2283
12.2878 93.1522
12.5036 89.3478
12.7194 85.2717
12.8633 82.2826
13.1511 78.7500
13.3669 75.2174
13.7266 71.1413
14.1583 67.0652
14.4460 63.8043
14.8058 60.8152
15.2374 56.7391
15.6691 53.7500
16.2446 50.2174
16.6763 47.7717
17.3957 44.2391
17.8993 41.7935
18.5468 39.0761
19.3381 35.8152
20.3453 32.5543
21.2806 29.8370
22.2158 27.9348
23.4388 25.7609
24.4460 23.8587
25.4532 22.7717
26.3885 21.6848
27.4676 21.1413
28.3309 20.8696
29.4101 20.3261
30.6331 20.5978
31.5683 20.8696
32.4317 21.4130
33.5108 22.2283
11.7842 105.1087
12.1439 97.2283
12.2878 93.1522
12.5036 89.3478
12.7194 85.2717
12.8633 82.2826
13.1511 78.7500
13.3669 75.2174
13.7266 71.1413
14.1583 67.0652
14.4460 63.8043
14.8058 60.8152
15.2374 56.7391
15.6691 53.7500
16.2446 50.2174
16.6763 47.7717
17.3957 44.2391
17.8993 41.7935
18.5468 39.0761
19.3381 35.8152
20.3453 32.5543
21.2806 29.8370
22.2158 27.9348
23.4388 25.7609
24.4460 23.8587
25.4532 22.7717
26.3885 21.6848
27.4676 21.1413
28.3309 20.8696
29.4101 20.3261
30.6331 20.5978
31.5683 20.8696
32.4317 21.4130
33.5108 22.2283
Параболой получается плохо.
745.80928 -108.84563*x + 6.33467*x^2 -0.16686*x^3 + 0.0016585*x^4
А вообще, сам исследователь должен решать, какая кривая ему подходит.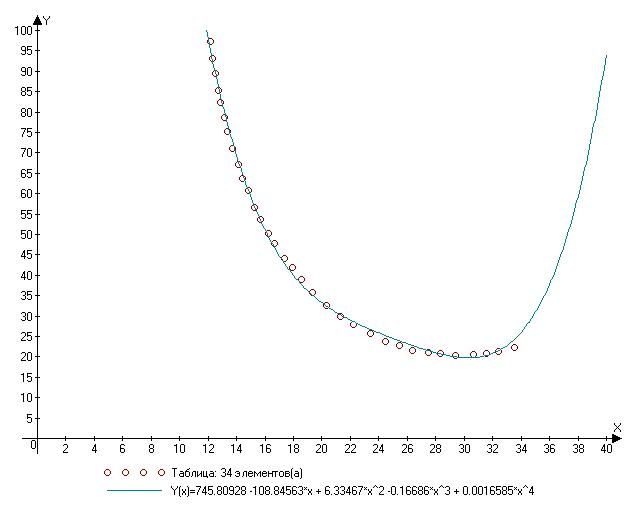
745.80928 -108.84563*x + 6.33467*x^2 -0.16686*x^3 + 0.0016585*x^4
А вообще, сам исследователь должен решать, какая кривая ему подходит.
Гипербола тут не подходит, т.к. правый конец загнут вверх - а у гиперболы не загнут. Если уж хочется гиперболу, то пробуй вида C1/(x-x1) + p*x - с небольшой линейной добавкой, чтобы конец правый был бы загнут вверх
Да, я забыла, что конец в верх загибается. Так что по вашему мнению лучше: последнее уравнение или предыдущее?
О, спасибо! Но вот 4-ая степень... Вообще, нужно будет в обратную сторону считать, для данного у подбирать х. Как будет обратная функция выглядеть?
Может, просто выбросить точки после 30? ТС ведь сказала, что а) они не слишком важны; б) теория предсказывает гиперболу (?)
ПС сорри, что так со стороны советую, никакого подходящего софта на компе нет(
ПС сорри, что так со стороны советую, никакого подходящего софта на компе нет(
вообще, я неправильно биологически сказала. После 30 градусов зародышам плохо и развитие замедляется, хотя с ростом температуры скорость развития до 30 градусов росла. Поэтому всё-таки парабола, а не гипербола.
Для обратной функции получается вот так:
58.75189 -2.30165*x + 0.04739*x^2 -4.46535*10^(-4)*x^3 +1.55877*10^(-6)*x^4
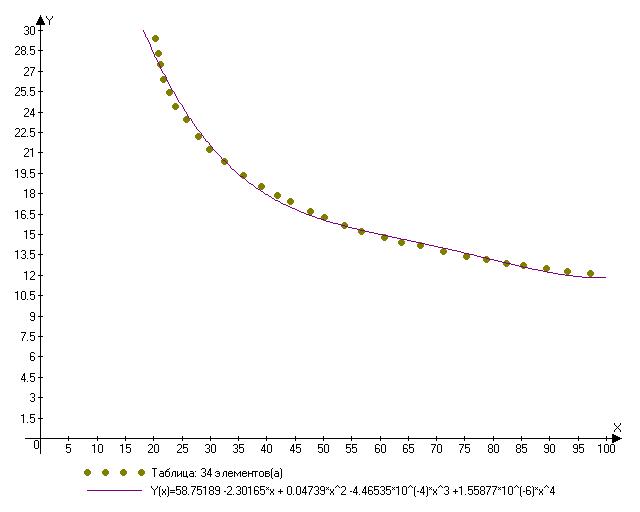
Для большей степени получается лучше, но я не могу заставить Origin выводить параметры с нужным мне числом знаков, а при большой степени формула сильно зависит от коэффициентов при старших степенях.
58.75189 -2.30165*x + 0.04739*x^2 -4.46535*10^(-4)*x^3 +1.55877*10^(-6)*x^4
Для большей степени получается лучше, но я не могу заставить Origin выводить параметры с нужным мне числом знаков, а при большой степени формула сильно зависит от коэффициентов при старших степенях.
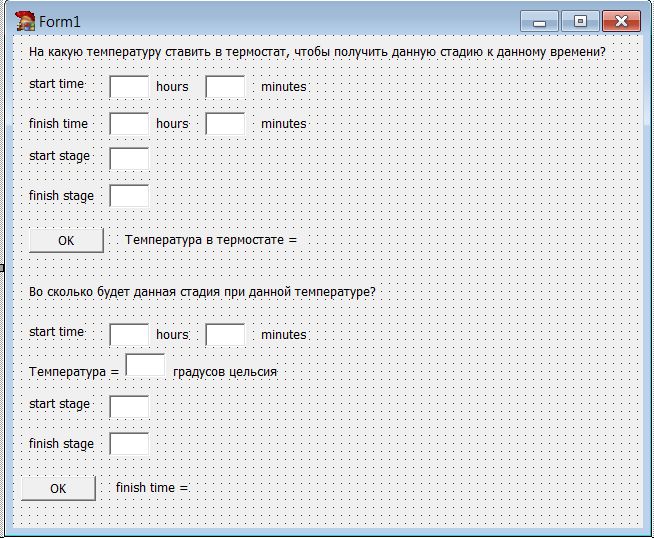
Спасибки! Вот начала уже себе эмбриологический калькулятор делать
а зачем тебе формула для такого
в этой задаче можно наверное просто кусочно-линейную интерполяцию взять
в этой задаче можно наверное просто кусочно-линейную интерполяцию взять
кстати да, это точнее будет
ну кусочно-линейная — это может и слишком большое упрощение, но про сплайны писали в самом начале. На самом деле тут дейсвительно нужны сплайны, одной функцией надо фиттить, когда есть какая-то теоретическая модель (соответственно вид функции) и надо зафиттив, получить неизвестные параметры из этого самого вида, которые имеют какое-то теоретическое значение. Мне так всегда казалось.
а зачем тебе формула для такогону, я как-то не занакома с этим... фитирование тока и пришло в голову
в этой задаче можно наверное просто кусочно-линейную интерполяцию взять
а авторы гарфика ведь как-то его проводили по данным? разве они не фитировали?
не, ну чтоб красивую кривую провести — тоже иногда. Со сплайнами может сильно гулять где не надо. Впрочем, мне кажется не приходилось для таких целей фитовать уравнением, обходился сплайнами, это же легче
есть какая-то теоретическая модельТеоретической модели нету. Вот всё, что есть - на картинке. Влом просто каждый раз считать отвечая на вопросы, что в форме... Вот и задумала такой калькулятор сделать.
Помнится на физпраке учили, что если для красоты — то проводить нужно только от руки В принципе, это правильно. Можно пользоваться софтом, поэтому, если потом нельзя отличить, от руки или нет. А ещё лучше вообще кривую не проводить, а оставить точки.
В принципе, это правильно. Можно пользоваться софтом, поэтому, если потом нельзя отличить, от руки или нет. А ещё лучше вообще кривую не проводить, а оставить точки.ну можно на каждом небольшом отрезке зафиттировать, это собственно и есть сплайн. И будет точно, это хорошо подходит для интерполяции (получения промежуточных значений даже подифференцировать можно, если очень хочется. А зачем подбирать глобально функцию одного фиксированного вида (полином 4й степени) — не совсем ясно.
Хотя, я вот подумал. Там же есть неточности, связанные с экспериментом, поэтому прямо линейную интерполяцию если делать, то будет нифига не точнее, поэтому я там выше враки, конечно, написал. Тут надо послушать каких-нибудь аццких экспериментаторов, они скажут что-нибудь здравое.
Хотя, я вот подумал. Там же есть неточности, связанные с экспериментом, поэтому прямо линейную интерполяцию если делать, то будет нифига не точнее, поэтому я там выше враки, конечно, написал. Тут надо послушать каких-нибудь аццких экспериментаторов, они скажут что-нибудь здравое.
Хотя, я вот подумал. Там же есть неточности, связанные с экспериментом, поэтому прямо линейную интерполяцию если делать, то будет нифига не точнее, поэтому я там выше враки, конечно, написал. Тут надо послушать каких-нибудь аццких экспериментаторов, они скажут что-нибудь здравое.Я не экспериментатор, но мне кажется, что формула, придуманная от балды (типа полином или что ещё взбредёт в голову ну совершенно ничего не прибавляет к экспериментальным данным.
Не прибавляет. Примерно поэтому нас и заставляли от руки — чтобы не придавали лишнего значения.
Короче, наверное я вспомнил, просто сам не изучал, но натыкался на статьи по непараметрической регрессии, это наверное близко к идеалу, но сильно мозголомно, поэтому здесь не в тему.
Да. Особая математическая точность не нужна. Т.к. даже очень точное математическое описание точного биологического результата не даст, т.к. скорость развития ещё и от особенностей каждой лягухи, которая давала эту икру зависит. Это так для прикидки.
вот мое уравнение :y=-2657,77 + 195,65x - 5,58254x^2 + 0,00199394x^4 - 0,000000000421538x^8 + 14068,5(1/x)
y Расчетные Остатки
1 105,1087 104,7126 0,3961
2 97,2283 96,5495 0,6788
3 93,1522 93,5827 -0,4305
4 89,3478 89,4231 -0,0753
5 85,2717 85,5840 -0,3123
6 82,2826 83,1883 -0,9057
7 78,7500 78,7567 -0,0067
8 75,2174 75,7206 -0,5032
9 71,1413 71,1428 -0,0015
10 67,0652 66,3373 0,7279
11 63,8043 63,4903 0,3140
12 60,8152 60,2698 0,5454
13 56,7391 56,8303 -0,0912
14 53,7500 53,7729 -0,0229
15 50,2174 50,1739 0,0435
16 47,7717 47,7601 0,0116
17 44,2391 44,1572 0,0819
18 41,7935 41,8812 -0,0877
19 39,0761 39,1895 -0,1134
20 35,8152 36,1975 -0,3823
21 32,5543 32,8018 -0,2475
22 29,8370 30,0474 -0,2104
23 27,9348 27,6913 0,2435
24 25,7609 25,2368 0,5241
25 23,8587 23,7408 0,1179
26 22,7717 22,6632 0,1085
27 21,6848 21,9498 -0,2650
28 21,1413 21,3349 -0,1936
29 20,8696 20,9183 -0,0487
30 20,3261 20,4712 -0,1451
31 20,5978 20,2919 0,3059
32 20,8696 20,7259 0,1437
33 21,4130 21,6659 -0,2529
34 22,2283 22,1752 0,0531
:) вот мое уравнение :Спасибо! Не очень понимаю, что такое расчётные остатки. А график этой кривой и точками данных можно увидеть, а то эту функцию сравнить на точность сложно с другими "решениями".
y=-2657,77 + 195,65x - 5,58254x^2 + 0,00199394x^4 - 0,000000000421538x^8 + 14068,5(1/x)
y Расчетные Остатки
расчетные - это значения У которые посчитаны по этой формуле,
а остатки - это расхождения между расчетными и фактическими
а остатки - это расхождения между расчетными и фактическими
vitamin23
Народ, подскажите, пож, биологу как и с помощью каких программ можно найти уравнение кривой ниже. Собственно, я графулой точки оцифровала, а чем фитировать не знаю: как подбирать функцию, которой будем фитировать? Можно пойти проще - найти уравнение собственно прорисованной кривой на графике (которая была вычислена исходя из экспериментальных точек но опять же: как это делается, в какой проге? У меня есть Matematica, Statistica. В них можно это сделать? Ещё есть дрова для Origin..Или если лень пояснять, уравнение кривой дайте хотя бы. Но хотелось бы знать, как это делается. А то достало каждый раз по графику на глаз точки искать. Проще подставить в формулу и узнать, в какую температуру зародышей помещать, чтобы к определённому времени получить нужную стадию развития. Если формула будет, то я тогда смоу в делфи стадийный калькулятор сделать Будет очень удобно. Зная время оплодотворения, стадию, которая нужна, время, к которому она нужна, можно вычислить на сколько градусов ставить термостат и др. виды расчётов делать. В общем, очень нужно это уравнение...